Question Number 162589 by mkam last updated on 30/Dec/21

Answered by Ar Brandon last updated on 30/Dec/21
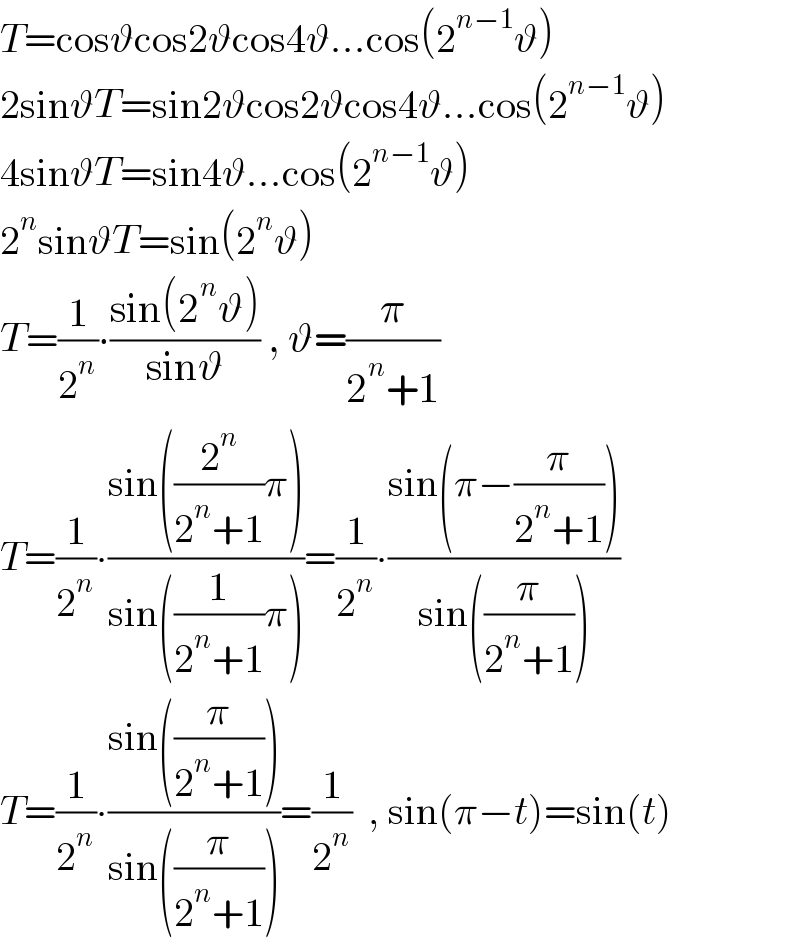
$${T}=\mathrm{cos}\vartheta\mathrm{cos2}\vartheta\mathrm{cos4}\vartheta…\mathrm{cos}\left(\mathrm{2}^{{n}−\mathrm{1}} \vartheta\right) \\ $$$$\mathrm{2sin}\vartheta{T}=\mathrm{sin2}\vartheta\mathrm{cos2}\vartheta\mathrm{cos4}\vartheta…\mathrm{cos}\left(\mathrm{2}^{{n}−\mathrm{1}} \vartheta\right) \\ $$$$\mathrm{4sin}\vartheta{T}=\mathrm{sin4}\vartheta…\mathrm{cos}\left(\mathrm{2}^{{n}−\mathrm{1}} \vartheta\right) \\ $$$$\mathrm{2}^{{n}} \mathrm{sin}\vartheta{T}=\mathrm{sin}\left(\mathrm{2}^{{n}} \vartheta\right) \\ $$$${T}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\centerdot\frac{\mathrm{sin}\left(\mathrm{2}^{{n}} \vartheta\right)}{\mathrm{sin}\vartheta}\:,\:\vartheta=\frac{\pi}{\mathrm{2}^{{n}} +\mathrm{1}} \\ $$$${T}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\centerdot\frac{\mathrm{sin}\left(\frac{\mathrm{2}^{{n}} }{\mathrm{2}^{{n}} +\mathrm{1}}\pi\right)}{\mathrm{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} +\mathrm{1}}\pi\right)}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\centerdot\frac{\mathrm{sin}\left(\pi−\frac{\pi}{\mathrm{2}^{{n}} +\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} +\mathrm{1}}\right)} \\ $$$${T}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\centerdot\frac{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} +\mathrm{1}}\right)}{\mathrm{sin}\left(\frac{\pi}{\mathrm{2}^{{n}} +\mathrm{1}}\right)}=\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\:,\:\mathrm{sin}\left(\pi−{t}\right)=\mathrm{sin}\left({t}\right) \\ $$
Commented by peter frank last updated on 31/Dec/21

$$\mathrm{thank}\:\mathrm{you} \\ $$
