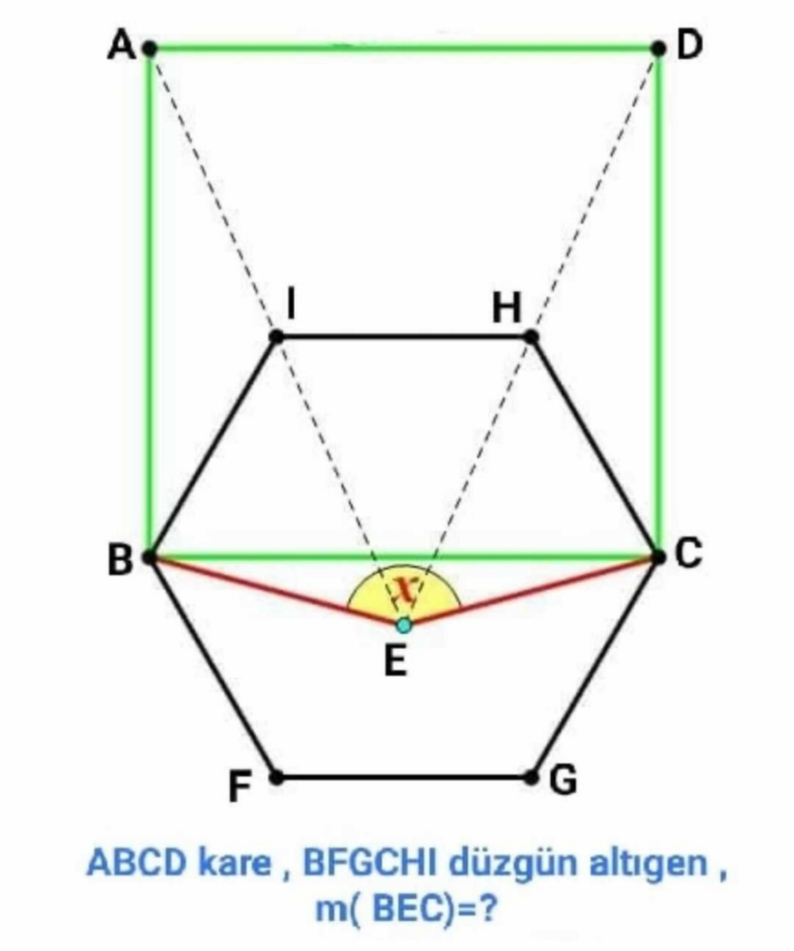
Question Number 162598 by amin96 last updated on 30/Dec/21
Answered by mr W last updated on 30/Dec/21
Commented by mr W last updated on 30/Dec/21

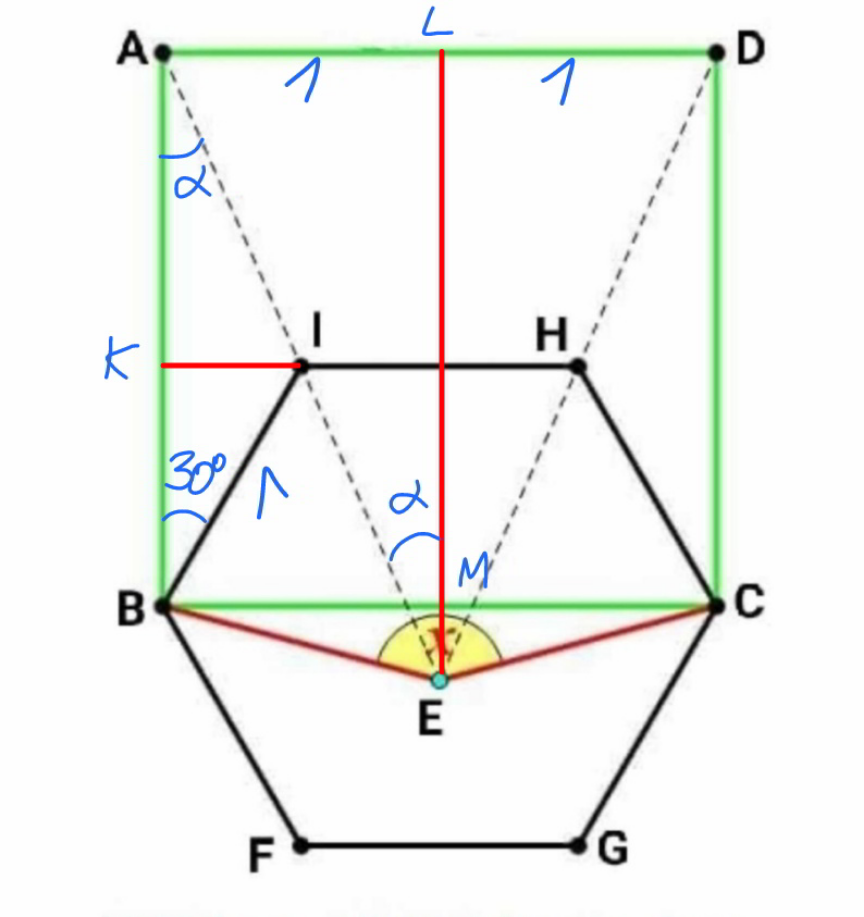
$${say}\:{side}\:{length}\:{of}\:{hexagon}\:{is}\:\mathrm{1}. \\ $$$${then}\:{the}\:{side}\:{length}\:{of}\:{square}\:{is}\:\mathrm{2}. \\ $$$${AK}=\mathrm{2}−\mathrm{1}×\mathrm{cos}\:\mathrm{30}°=\mathrm{2}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\alpha=\frac{{KI}}{{AK}}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}=\frac{\mathrm{1}}{\mathrm{4}−\sqrt{\mathrm{3}}} \\ $$$${LE}=\frac{{AL}}{\mathrm{tan}\:\alpha}=\mathrm{4}−\sqrt{\mathrm{3}} \\ $$$${ME}={LE}−\mathrm{2}=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\:\frac{{x}}{\mathrm{2}}=\frac{{BM}}{{ME}}=\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}=\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\mathrm{1}−\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{2}} }=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\mathrm{180}°−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}=\mathrm{180}°−\mathrm{30}°=\mathrm{150}° \\ $$
Commented by amin96 last updated on 30/Dec/21
$${thanks}\:{sir}.\:{greatful} \\ $$
Commented by Tawa11 last updated on 30/Dec/21
$$\mathrm{Great}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you} \\ $$
