Menu Close

Question-162785

Tinku Tara 0 Comments
Pin




Question Number 162785 by john_santu last updated on 01/Jan/22
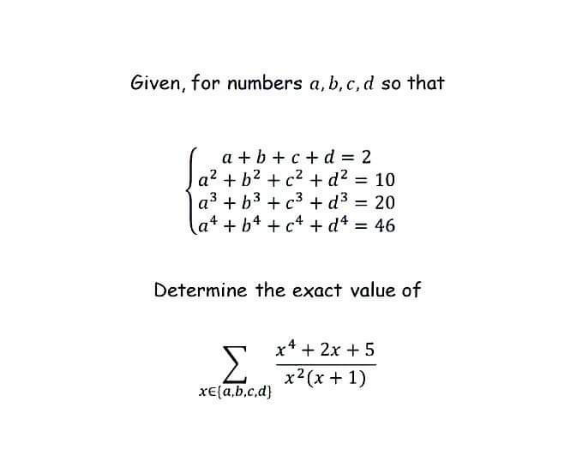
Answered by Rasheed.Sindhi last updated on 02/Jan/22
((x^4 +2x+5)/(x^2 (x+1)))=(x−1)+((x^2 +2x+5)/(x^2 (x+1))) ((x^2 +2x+5)/(x^2 (x+1)))=(A_1 /x)+(A_2 /x^2 )+(B/(x+1)) A_1 x(x+1)+A_2 (x+1)+Bx^2 =x^2 +2x+5 x=0:A_2 (0+1)=0^2 +2.0+5=5 A_2 =5 x=−1:B(−1)^2 =(−1)^2 +2(−1)+5 B=4 A_1 x^2 +A_1 x+A_2 x+A_2 +Bx^2 =x^2 +2x+5 (A_1 +B)x^2 +(A_1 +A_2 )x+A_2 =x^2 +2x+5 A_1 +B=1 , A_1 +A_2 =2 , A_2 =5 A_1 +B=1⇒A_1 +4=1⇒A_1 =−3 A_1 +A_2 =2⇒−3+5=2 ✓ ((x^4 +2x+5)/(x^2 (x+1)))=(x−1)+((x^2 +2x+5)/(x^2 (x+1))) =x−(3/x)+(5/x^2 )+(4/(x+1))−1 Σ_(x∈{a,b,c,d}) ((x^4 +2x+5)/(x^2 (x+1)))=Σ_(x∈{a,b,c,d}) x−Σ_(x∈{a,b,c,d}) (3/x) +Σ_(x∈{a,b,c,d}) (5/x^2 )+Σ_(x∈{a,b,c,d}) +Σ_(x∈{a,b,c,d}) (4/(x+1)) Σ_(x∈{a,b,c,d}) ((x^4 +2x+5)/(x^2 (x+1)))=−1+(Σ_(x∈{a,b,c,d}) x)− 3(Σ_(x∈{a,b,c,d}) (1/x)) +5(Σ_(x∈{a,b,c,d}) (1/x^2 )) +4Σ_(x∈{a,b,c,d}) (1/(x+1)) =−1+(a+b+c+d) −3((1/a)+(1/b)+(1/c)+(1/d)) +5((1/a^2 )+(1/b^2 )+(1/c^2 )+(1/d^2 )) +4((1/(a+1))+(1/(b+1))+(1/(c+1))+(1/(d+1))) .... ...
$$ \\ $$$$\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}=\left({x}−\mathrm{1}\right)+\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)} \\ $$$$\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}=\frac{{A}_{\mathrm{1}} }{{x}}+\frac{{A}_{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{{B}}{{x}+\mathrm{1}} \\ $$$${A}_{\mathrm{1}} {x}\left({x}+\mathrm{1}\right)+{A}_{\mathrm{2}} \left({x}+\mathrm{1}\right)+{Bx}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5} \\ $$$${x}=\mathrm{0}:{A}_{\mathrm{2}} \left(\mathrm{0}+\mathrm{1}\right)=\mathrm{0}^{\mathrm{2}} +\mathrm{2}.\mathrm{0}+\mathrm{5}=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{A}_{\mathrm{2}} =\mathrm{5} \\ $$$${x}=−\mathrm{1}:{B}\left(−\mathrm{1}\right)^{\mathrm{2}} =\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{2}\left(−\mathrm{1}\right)+\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{B}=\mathrm{4} \\ $$$${A}_{\mathrm{1}} {x}^{\mathrm{2}} +{A}_{\mathrm{1}} {x}+{A}_{\mathrm{2}} {x}+{A}_{\mathrm{2}} +{Bx}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5} \\ $$$$\left({A}_{\mathrm{1}} +{B}\right){x}^{\mathrm{2}} +\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} \right){x}+{A}_{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5} \\ $$$${A}_{\mathrm{1}} +{B}=\mathrm{1}\:,\:{A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\mathrm{2}\:\:,\:{A}_{\mathrm{2}} =\mathrm{5} \\ $$$${A}_{\mathrm{1}} +{B}=\mathrm{1}\Rightarrow{A}_{\mathrm{1}} +\mathrm{4}=\mathrm{1}\Rightarrow{A}_{\mathrm{1}} =−\mathrm{3} \\ $$$${A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\mathrm{2}\Rightarrow−\mathrm{3}+\mathrm{5}=\mathrm{2}\:\checkmark \\ $$$$\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}=\left({x}−\mathrm{1}\right)+\frac{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)} \\ $$$$\:\:\:\:={x}−\frac{\mathrm{3}}{{x}}+\frac{\mathrm{5}}{{x}^{\mathrm{2}} }+\frac{\mathrm{4}}{{x}+\mathrm{1}}−\mathrm{1} \\ $$$$\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\sum}\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}=\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:{x}−\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\frac{\mathrm{3}}{{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\:\:\frac{\mathrm{5}}{{x}^{\mathrm{2}} }+\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\:+\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\:\:\frac{\mathrm{4}}{{x}+\mathrm{1}} \\ $$$$\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\sum}\frac{{x}^{\mathrm{4}} +\mathrm{2}{x}+\mathrm{5}}{{x}^{\mathrm{2}} \left({x}+\mathrm{1}\right)}=−\mathrm{1}+\left(\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:{x}\right)−\:\mathrm{3}\left(\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\frac{\mathrm{1}}{{x}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:+\mathrm{5}\left(\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)\:+\mathrm{4}\underset{{x}\in\left\{{a},{b},{c},{d}\right\}} {\Sigma}\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}+\mathrm{1}} \\ $$$$=−\mathrm{1}+\left({a}+{b}+{c}+{d}\right) \\ $$$$\:\:\:\:\:−\mathrm{3}\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}+\frac{\mathrm{1}}{{d}}\right) \\ $$$$\:\:\:\:+\mathrm{5}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\frac{\mathrm{1}}{{b}^{\mathrm{2}} }+\frac{\mathrm{1}}{{c}^{\mathrm{2}} }+\frac{\mathrm{1}}{{d}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:\:+\mathrm{4}\left(\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{1}}{{b}+\mathrm{1}}+\frac{\mathrm{1}}{{c}+\mathrm{1}}+\frac{\mathrm{1}}{{d}+\mathrm{1}}\right) \\ $$$$ \\ $$$$…. \\ $$$$… \\ $$
Commented by Rasheed.Sindhi last updated on 03/Jan/22
Thanks miss tawa, your compliments matters for me!
$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{miss}}\:\boldsymbol{\mathrm{tawa}}, \\ $$$${your}\:{compliments}\:{matters}\:{for}\:{me}! \\ $$
Commented by Tawa11 last updated on 03/Jan/22
Weldone sir
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$
Commented by Tawa11 last updated on 04/Jan/22
I usually learn from your solutions sir. God bless you more.
$$\mathrm{I}\:\mathrm{usually}\:\mathrm{learn}\:\mathrm{from}\:\mathrm{your}\:\mathrm{solutions}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{more}. \\ $$
Commented by Rasheed.Sindhi last updated on 04/Jan/22
Thanks Miss! Iappreciate your contribution to to forum & your encouraging others. GOD BLESS YOU ALSO!
$$\mathbb{T}\boldsymbol{\mathrm{hanks}}\:\boldsymbol{\mathrm{Miss}}!\:\mathrm{Iappreciate}\:\mathrm{your}\:\mathrm{contribution}\:\mathrm{to}\: \\ $$$$\mathrm{to}\:\mathrm{forum}\:\&\:\mathrm{your}\:\mathrm{encouraging}\:\mathrm{others}. \\ $$$$\boldsymbol{\mathrm{GOD}}\:\boldsymbol{\mathrm{BLESS}}\:\boldsymbol{\mathrm{YOU}}\:\boldsymbol{\mathrm{ALSO}}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *