Question Number 162791 by mnjuly1970 last updated on 01/Jan/22

Answered by amin96 last updated on 01/Jan/22
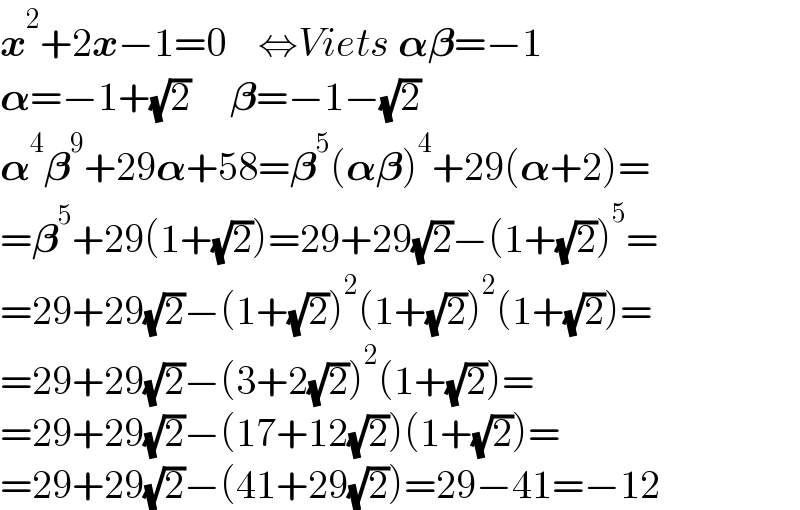
$$\boldsymbol{{x}}^{\mathrm{2}} +\mathrm{2}\boldsymbol{{x}}−\mathrm{1}=\mathrm{0}\:\:\:\:\Leftrightarrow{Viets}\:\boldsymbol{\alpha\beta}=−\mathrm{1} \\ $$$$\boldsymbol{\alpha}=−\mathrm{1}+\sqrt{\mathrm{2}}\:\:\:\:\:\boldsymbol{\beta}=−\mathrm{1}−\sqrt{\mathrm{2}} \\ $$$$\boldsymbol{\alpha}^{\mathrm{4}} \boldsymbol{\beta}^{\mathrm{9}} +\mathrm{29}\boldsymbol{\alpha}+\mathrm{58}=\boldsymbol{\beta}^{\mathrm{5}} \left(\boldsymbol{\alpha\beta}\right)^{\mathrm{4}} +\mathrm{29}\left(\boldsymbol{\alpha}+\mathrm{2}\right)= \\ $$$$=\boldsymbol{\beta}^{\mathrm{5}} +\mathrm{29}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\mathrm{29}+\mathrm{29}\sqrt{\mathrm{2}}−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{5}} = \\ $$$$=\mathrm{29}+\mathrm{29}\sqrt{\mathrm{2}}−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\right)= \\ $$$$=\mathrm{29}+\mathrm{29}\sqrt{\mathrm{2}}−\left(\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left(\mathrm{1}+\sqrt{\mathrm{2}}\right)= \\ $$$$=\mathrm{29}+\mathrm{29}\sqrt{\mathrm{2}}−\left(\mathrm{17}+\mathrm{12}\sqrt{\mathrm{2}}\right)\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)= \\ $$$$=\mathrm{29}+\mathrm{29}\sqrt{\mathrm{2}}−\left(\mathrm{41}+\mathrm{29}\sqrt{\mathrm{2}}\right)=\mathrm{29}−\mathrm{41}=−\mathrm{12} \\ $$
Commented by mnjuly1970 last updated on 01/Jan/22
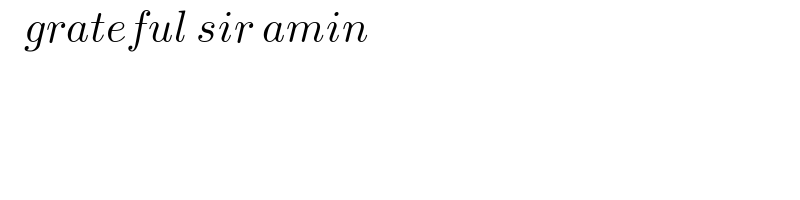
$$\:\:\:{grateful}\:{sir}\:{amin} \\ $$
Answered by alephzero last updated on 01/Jan/22
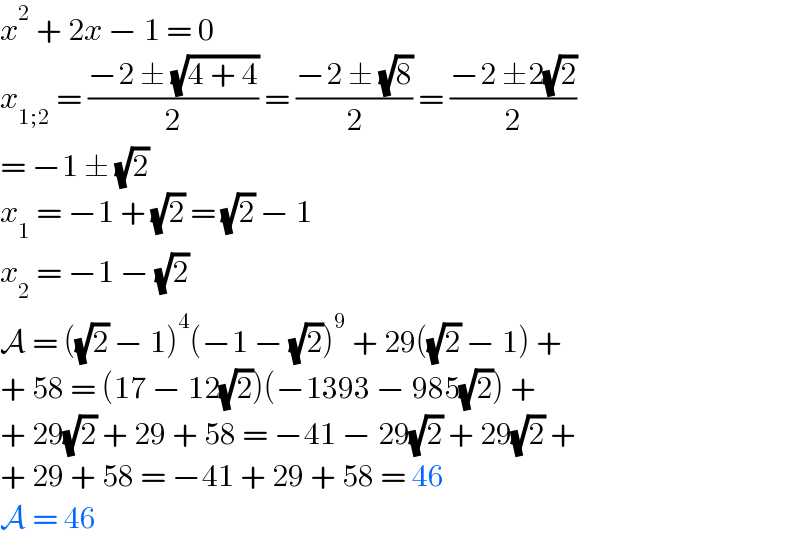
$${x}^{\mathrm{2}} \:+\:\mathrm{2}{x}\:−\:\mathrm{1}\:=\:\mathrm{0} \\ $$$${x}_{\mathrm{1};\mathrm{2}} \:=\:\frac{−\mathrm{2}\:\pm\:\sqrt{\mathrm{4}\:+\:\mathrm{4}}}{\mathrm{2}}\:=\:\frac{−\mathrm{2}\:\pm\:\sqrt{\mathrm{8}}}{\mathrm{2}}\:=\:\frac{−\mathrm{2}\:\pm\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$=\:−\mathrm{1}\:\pm\:\sqrt{\mathrm{2}} \\ $$$${x}_{\mathrm{1}} \:=\:−\mathrm{1}\:+\:\sqrt{\mathrm{2}}\:=\:\sqrt{\mathrm{2}}\:−\:\mathrm{1} \\ $$$${x}_{\mathrm{2}} \:=\:−\mathrm{1}\:−\:\sqrt{\mathrm{2}} \\ $$$$\mathcal{A}\:=\:\left(\sqrt{\mathrm{2}}\:−\:\mathrm{1}\right)^{\mathrm{4}} \left(−\mathrm{1}\:−\:\sqrt{\mathrm{2}}\right)^{\mathrm{9}} \:+\:\mathrm{29}\left(\sqrt{\mathrm{2}}\:−\:\mathrm{1}\right)\:+\: \\ $$$$+\:\mathrm{58}\:=\:\left(\mathrm{17}\:−\:\mathrm{12}\sqrt{\mathrm{2}}\right)\left(−\mathrm{1393}\:−\:\mathrm{985}\sqrt{\mathrm{2}}\right)\:+\: \\ $$$$+\:\mathrm{29}\sqrt{\mathrm{2}}\:+\:\mathrm{29}\:+\:\mathrm{58}\:=\:−\mathrm{41}\:−\:\mathrm{29}\sqrt{\mathrm{2}}\:+\:\mathrm{29}\sqrt{\mathrm{2}}\:+ \\ $$$$+\:\mathrm{29}\:+\:\mathrm{58}\:=\:−\mathrm{41}\:+\:\mathrm{29}\:+\:\mathrm{58}\:=\:\mathrm{46} \\ $$$$\mathcal{A}\:=\:\mathrm{46} \\ $$
Answered by mindispower last updated on 01/Jan/22
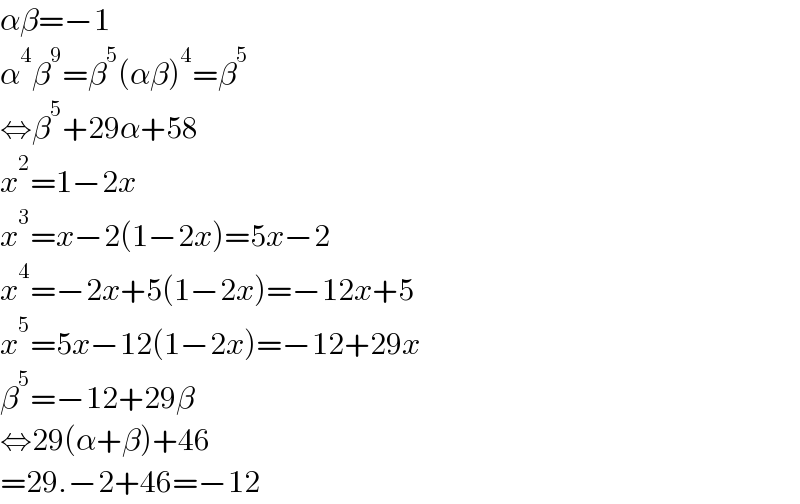
$$\alpha\beta=−\mathrm{1} \\ $$$$\alpha^{\mathrm{4}} \beta^{\mathrm{9}} =\beta^{\mathrm{5}} \left(\alpha\beta\right)^{\mathrm{4}} =\beta^{\mathrm{5}} \\ $$$$\Leftrightarrow\beta^{\mathrm{5}} +\mathrm{29}\alpha+\mathrm{58} \\ $$$${x}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{x} \\ $$$${x}^{\mathrm{3}} ={x}−\mathrm{2}\left(\mathrm{1}−\mathrm{2}{x}\right)=\mathrm{5}{x}−\mathrm{2} \\ $$$${x}^{\mathrm{4}} =−\mathrm{2}{x}+\mathrm{5}\left(\mathrm{1}−\mathrm{2}{x}\right)=−\mathrm{12}{x}+\mathrm{5} \\ $$$${x}^{\mathrm{5}} =\mathrm{5}{x}−\mathrm{12}\left(\mathrm{1}−\mathrm{2}{x}\right)=−\mathrm{12}+\mathrm{29}{x} \\ $$$$\beta^{\mathrm{5}} =−\mathrm{12}+\mathrm{29}\beta \\ $$$$\Leftrightarrow\mathrm{29}\left(\alpha+\beta\right)+\mathrm{46} \\ $$$$=\mathrm{29}.−\mathrm{2}+\mathrm{46}=−\mathrm{12} \\ $$
Commented by mnjuly1970 last updated on 01/Jan/22
$${bravo}\:{sir}\:{power}\:…{this}\:{solution}\: \\ $$$$\:\:{is}\:{very}\:{nice}… \\ $$
