Question Number 162833 by mkam last updated on 01/Jan/22

Answered by abdullahhhhh last updated on 01/Jan/22
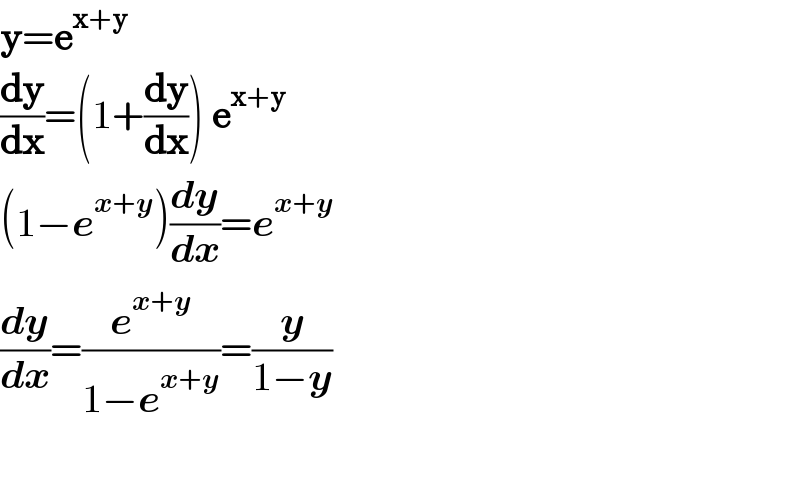
$$\boldsymbol{\mathrm{y}}=\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}} \\ $$$$\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}=\left(\mathrm{1}+\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\right)\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}} \\ $$$$\left(\mathrm{1}−\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{y}}} \right)\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{y}}} \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}=\frac{\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{y}}} }{\mathrm{1}−\boldsymbol{{e}}^{\boldsymbol{{x}}+\boldsymbol{{y}}} }=\frac{\boldsymbol{{y}}}{\mathrm{1}−\boldsymbol{{y}}} \\ $$$$ \\ $$
Commented by abdullahhhhh last updated on 01/Jan/22
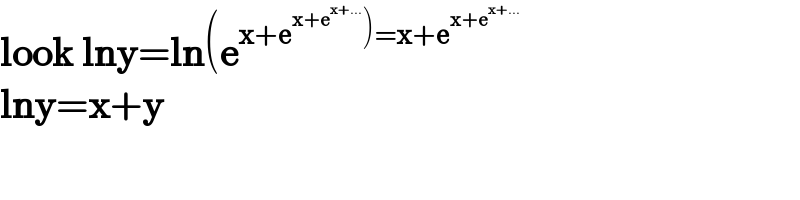
$$\boldsymbol{\mathrm{look}}\:\boldsymbol{\mathrm{lny}}=\boldsymbol{\mathrm{ln}}\left(\boldsymbol{\mathrm{e}}^{\left.\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+…} } \right)=\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}+…} } } \right. \\ $$$$\boldsymbol{\mathrm{lny}}=\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{y}}\:\: \\ $$$$ \\ $$
Commented by mkam last updated on 01/Jan/22
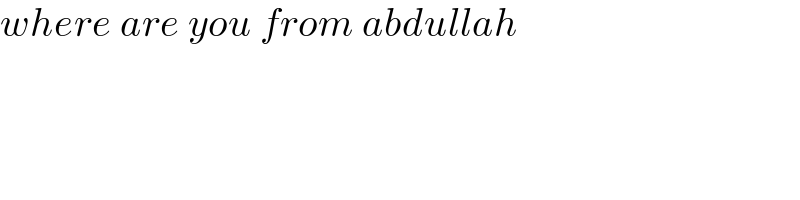
$${where}\:{are}\:{you}\:{from}\:{abdullah} \\ $$
Commented by mkam last updated on 01/Jan/22

$${how}\:{y}\:=\:{e}^{{x}+{y}} \:? \\ $$
Commented by abdullahhhhh last updated on 01/Jan/22

$$\boldsymbol{\mathrm{from}}\:\boldsymbol{\mathrm{egypt}} \\ $$
Commented by mkam last updated on 01/Jan/22
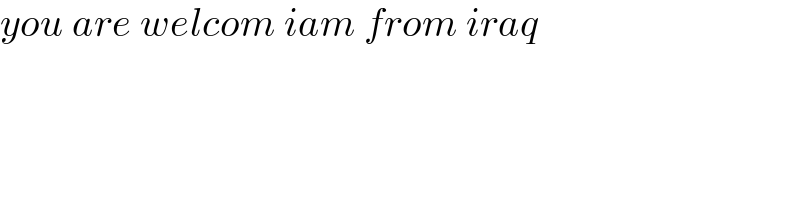
$${you}\:{are}\:{welcom}\:{iam}\:{from}\:{iraq} \\ $$
Commented by mkam last updated on 01/Jan/22

$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$
