Menu Close

Question-162860

Tinku Tara 0 Comments
Pin




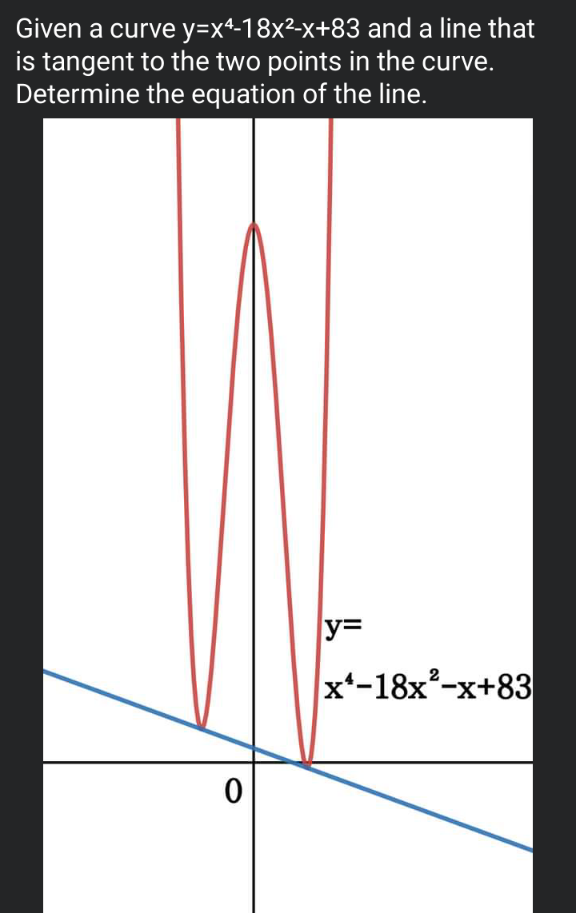
Question Number 162860 by Mathematification last updated on 01/Jan/22
Answered by MJS_new last updated on 01/Jan/22
f(x)=x^4 −18x^2 −x+83 g(x)=c_1 x+c_0 h(x)=f(x)−g(x)=x^4 −18x^2 −(c_1 +1)x+(83−c_0 ) we know h(x) must have 2 minima m_1 , m_2 and 1 maximum at x=((m_1 +m_2 )/2) ⇒ h′(x)=C(x−m_1 )(x−m_2 )(x−((m_1 +m_2 )/2))=0 ⇔ x^3 −((3(m_1 +m_2 ))/2)x^2 +((m_1 ^2 +4m_1 m_2 +m_2 ^3 )/2)x−((m_1 (m_1 +m_2 )m_2 )/2)=0 but h′(x)=4x^3 −36x−(c_1 +1) ⇒ x^3 −9x−((c_1 +1)/4)=0 ⇒ −((3(m_1 +m_2 ))/2)=0 ⇒ m_2 =−m_1 ⇒ h(x)=x^3 −m_1 ^2 x=0 ⇒ m_1 =±3∧c_1 =−1 ⇒ g(x) touches f(x) at x=±3 now we easily get the tangent g(x)=−x+2
$${f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} −{x}+\mathrm{83} \\ $$$${g}\left({x}\right)={c}_{\mathrm{1}} {x}+{c}_{\mathrm{0}} \\ $$$${h}\left({x}\right)={f}\left({x}\right)−{g}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} −\left({c}_{\mathrm{1}} +\mathrm{1}\right){x}+\left(\mathrm{83}−{c}_{\mathrm{0}} \right) \\ $$$$\mathrm{we}\:\mathrm{know}\:{h}\left({x}\right)\:\mathrm{must}\:\mathrm{have}\:\mathrm{2}\:\mathrm{minima}\:{m}_{\mathrm{1}} ,\:{m}_{\mathrm{2}} \\ $$$$\mathrm{and}\:\mathrm{1}\:\mathrm{maximum}\:\mathrm{at}\:{x}=\frac{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${h}'\left({x}\right)={C}\left({x}−{m}_{\mathrm{1}} \right)\left({x}−{m}_{\mathrm{2}} \right)\left({x}−\frac{{m}_{\mathrm{1}} +{m}_{\mathrm{2}} }{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Leftrightarrow \\ $$$${x}^{\mathrm{3}} −\frac{\mathrm{3}\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right)}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{{m}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{4}{m}_{\mathrm{1}} {m}_{\mathrm{2}} +{m}_{\mathrm{2}} ^{\mathrm{3}} }{\mathrm{2}}{x}−\frac{{m}_{\mathrm{1}} \left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right){m}_{\mathrm{2}} }{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{but} \\ $$$${h}'\left({x}\right)=\mathrm{4}{x}^{\mathrm{3}} −\mathrm{36}{x}−\left({c}_{\mathrm{1}} +\mathrm{1}\right) \\ $$$$\Rightarrow \\ $$$${x}^{\mathrm{3}} −\mathrm{9}{x}−\frac{{c}_{\mathrm{1}} +\mathrm{1}}{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$−\frac{\mathrm{3}\left({m}_{\mathrm{1}} +{m}_{\mathrm{2}} \right)}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\:{m}_{\mathrm{2}} =−{m}_{\mathrm{1}} \\ $$$$\Rightarrow \\ $$$${h}\left({x}\right)={x}^{\mathrm{3}} −{m}_{\mathrm{1}} ^{\mathrm{2}} {x}=\mathrm{0}\:\Rightarrow\:{m}_{\mathrm{1}} =\pm\mathrm{3}\wedge{c}_{\mathrm{1}} =−\mathrm{1} \\ $$$$\Rightarrow\:{g}\left({x}\right)\:\mathrm{touches}\:{f}\left({x}\right)\:\mathrm{at}\:{x}=\pm\mathrm{3} \\ $$$$\mathrm{now}\:\mathrm{we}\:\mathrm{easily}\:\mathrm{get}\:\mathrm{the}\:\mathrm{tangent} \\ $$$${g}\left({x}\right)=−{x}+\mathrm{2} \\ $$
Commented by Tawa11 last updated on 02/Jan/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Answered by mr W last updated on 02/Jan/22
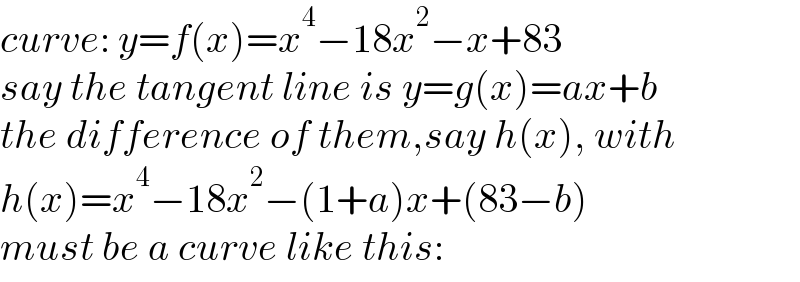
curve: y=f(x)=x^4 −18x^2 −x+83 say the tangent line is y=g(x)=ax+b the difference of them,say h(x), with h(x)=x^4 −18x^2 −(1+a)x+(83−b) must be a curve like this:
$${curve}:\:{y}={f}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} −{x}+\mathrm{83} \\ $$$${say}\:{the}\:{tangent}\:{line}\:{is}\:{y}={g}\left({x}\right)={ax}+{b} \\ $$$${the}\:{difference}\:{of}\:{them},{say}\:{h}\left({x}\right),\:{with} \\ $$$${h}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} −\left(\mathrm{1}+{a}\right){x}+\left(\mathrm{83}−{b}\right) \\ $$$${must}\:{be}\:{a}\:{curve}\:{like}\:{this}: \\ $$
Commented by mr W last updated on 02/Jan/22
Commented by mr W last updated on 02/Jan/22
let′s have a close look at it. the curve has two zeros, say p and q. at these two points the curve tangents also the x−axis. that means at these two points the curve has minimum which is also zero. we can assume then h(x)=(x−p)(x−q)(x^2 +ux+v) h′(x)=(x−p)(x−q)(2x+u)+(2x−p−q)(x^2 +ux+v) we have h′(p)=(p−q)(p^2 +up+v)=0 ⇒p^2 +up+v=0 h′(q)=(q−p)(q^2 +uq+v)=0 ⇒q^2 +uq+v=0 that means p, q are also roots of x^2 +ux+v=0, i.e. x^2 +ux+v=(x−p)(x−q). therefore h(x)=(x−p)(x−q)(x^2 +ux+v) ⇒h(x)=(x−p)^2 (x−q)^2 h′(x)=4(x−p)(x−q)(x−((p+q)/2)) that means h′(x)=0 at x=r=((p+q)/2). this is the point where the curve h(x) has local maximum. using these knowledges: h(x)=x^4 −18x^2 −(1+a)x+(83−b) h′(x)=4(x^3 −9x−((1+a)/4))=0 (x^3 −9x−((1+a)/4))=(x−p)(x−q)(x−((p+q)/2)) p+q+((p+q)/2)=0 ⇒p+q=0 pq+(p+q)((p+q)/2)=−9 ⇒pq=−9 ((pq(p+q))/2)=((1+a)/4) ⇒a=−1 ⇒p=3, q=−3 h(3)=h(−3)=0 ⇒3^4 −18×3^2 +83−b=0 ⇒b=2 ⇒the tangent line is y=−x+2 alternative way: we know that h(x) should be of the form h(x)=(x−p)^2 (x−q)^2 . that meams if it has no x^3 term, then it should also have no x term, i.e. 1+a=0, or a=−1. h(x)=x^4 −18x^2 +(83−b)=^(!) (x^2 −9^2 )^2 83−b=9^2 ⇒b=2
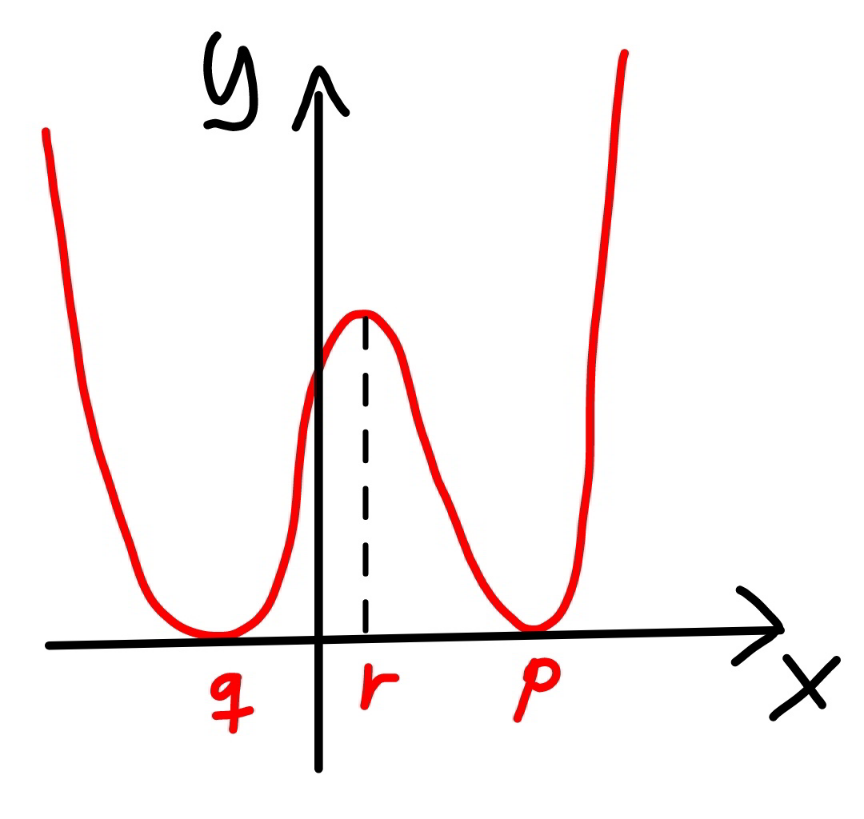
$${let}'{s}\:{have}\:{a}\:{close}\:{look}\:{at}\:{it}. \\ $$$${the}\:{curve}\:{has}\:{two}\:{zeros},\:{say}\:{p}\:{and}\:{q}. \\ $$$${at}\:{these}\:{two}\:{points}\:{the}\:{curve}\:{tangents} \\ $$$${also}\:{the}\:{x}−{axis}.\:{that}\:{means}\:{at}\:{these} \\ $$$${two}\:{points}\:{the}\:{curve}\:{has}\:{minimum} \\ $$$${which}\:{is}\:{also}\:{zero}. \\ $$$${we}\:{can}\:{assume}\:{then} \\ $$$${h}\left({x}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left({x}^{\mathrm{2}} +{ux}+{v}\right) \\ $$$${h}'\left({x}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left(\mathrm{2}{x}+{u}\right)+\left(\mathrm{2}{x}−{p}−{q}\right)\left({x}^{\mathrm{2}} +{ux}+{v}\right) \\ $$$${we}\:{have} \\ $$$${h}'\left({p}\right)=\left({p}−{q}\right)\left({p}^{\mathrm{2}} +{up}+{v}\right)=\mathrm{0}\: \\ $$$$\Rightarrow{p}^{\mathrm{2}} +{up}+{v}=\mathrm{0} \\ $$$${h}'\left({q}\right)=\left({q}−{p}\right)\left({q}^{\mathrm{2}} +{uq}+{v}\right)=\mathrm{0}\: \\ $$$$\Rightarrow{q}^{\mathrm{2}} +{uq}+{v}=\mathrm{0} \\ $$$${that}\:{means}\:{p},\:{q}\:{are}\:{also}\:{roots}\:{of} \\ $$$${x}^{\mathrm{2}} +{ux}+{v}=\mathrm{0},\:{i}.{e}. \\ $$$${x}^{\mathrm{2}} +{ux}+{v}=\left({x}−{p}\right)\left({x}−{q}\right). \\ $$$${therefore} \\ $$$${h}\left({x}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left({x}^{\mathrm{2}} +{ux}+{v}\right) \\ $$$$\Rightarrow{h}\left({x}\right)=\left({x}−{p}\right)^{\mathrm{2}} \left({x}−{q}\right)^{\mathrm{2}} \\ $$$${h}'\left({x}\right)=\mathrm{4}\left({x}−{p}\right)\left({x}−{q}\right)\left({x}−\frac{{p}+{q}}{\mathrm{2}}\right) \\ $$$${that}\:{means}\:{h}'\left({x}\right)=\mathrm{0}\:{at}\:{x}={r}=\frac{{p}+{q}}{\mathrm{2}}. \\ $$$${this}\:{is}\:{the}\:{point}\:{where}\:{the}\:{curve}\:{h}\left({x}\right) \\ $$$${has}\:{local}\:{maximum}. \\ $$$$ \\ $$$${using}\:{these}\:{knowledges}: \\ $$$${h}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} −\left(\mathrm{1}+{a}\right){x}+\left(\mathrm{83}−{b}\right) \\ $$$${h}'\left({x}\right)=\mathrm{4}\left({x}^{\mathrm{3}} −\mathrm{9}{x}−\frac{\mathrm{1}+{a}}{\mathrm{4}}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{3}} −\mathrm{9}{x}−\frac{\mathrm{1}+{a}}{\mathrm{4}}\right)=\left({x}−{p}\right)\left({x}−{q}\right)\left({x}−\frac{{p}+{q}}{\mathrm{2}}\right) \\ $$$${p}+{q}+\frac{{p}+{q}}{\mathrm{2}}=\mathrm{0}\:\Rightarrow{p}+{q}=\mathrm{0} \\ $$$${pq}+\left({p}+{q}\right)\frac{{p}+{q}}{\mathrm{2}}=−\mathrm{9}\:\Rightarrow{pq}=−\mathrm{9} \\ $$$$\frac{{pq}\left({p}+{q}\right)}{\mathrm{2}}=\frac{\mathrm{1}+{a}}{\mathrm{4}}\:\Rightarrow{a}=−\mathrm{1} \\ $$$$\Rightarrow{p}=\mathrm{3},\:{q}=−\mathrm{3} \\ $$$${h}\left(\mathrm{3}\right)={h}\left(−\mathrm{3}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{4}} −\mathrm{18}×\mathrm{3}^{\mathrm{2}} +\mathrm{83}−{b}=\mathrm{0}\:\Rightarrow{b}=\mathrm{2} \\ $$$$ \\ $$$$\Rightarrow{the}\:{tangent}\:{line}\:{is}\:{y}=−{x}+\mathrm{2} \\ $$$$ \\ $$$${alternative}\:{way}: \\ $$$${we}\:{know}\:{that}\:{h}\left({x}\right)\:{should}\:{be}\:{of}\:{the} \\ $$$${form}\:{h}\left({x}\right)=\left({x}−{p}\right)^{\mathrm{2}} \left({x}−{q}\right)^{\mathrm{2}} .\:{that} \\ $$$${meams}\:{if}\:{it}\:{has}\:{no}\:{x}^{\mathrm{3}} \:{term},\:{then}\:{it} \\ $$$${should}\:{also}\:{have}\:{no}\:{x}\:{term},\: \\ $$$${i}.{e}.\:\mathrm{1}+{a}=\mathrm{0},\:{or}\:{a}=−\mathrm{1}. \\ $$$${h}\left({x}\right)={x}^{\mathrm{4}} −\mathrm{18}{x}^{\mathrm{2}} +\left(\mathrm{83}−{b}\right)\overset{!} {=}\left({x}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\mathrm{83}−{b}=\mathrm{9}^{\mathrm{2}} \:\Rightarrow{b}=\mathrm{2} \\ $$
Commented by mr W last updated on 02/Jan/22
Commented by mr W last updated on 02/Jan/22
basically it′s the same solution as that from MJS sir, i just put some more explanation.
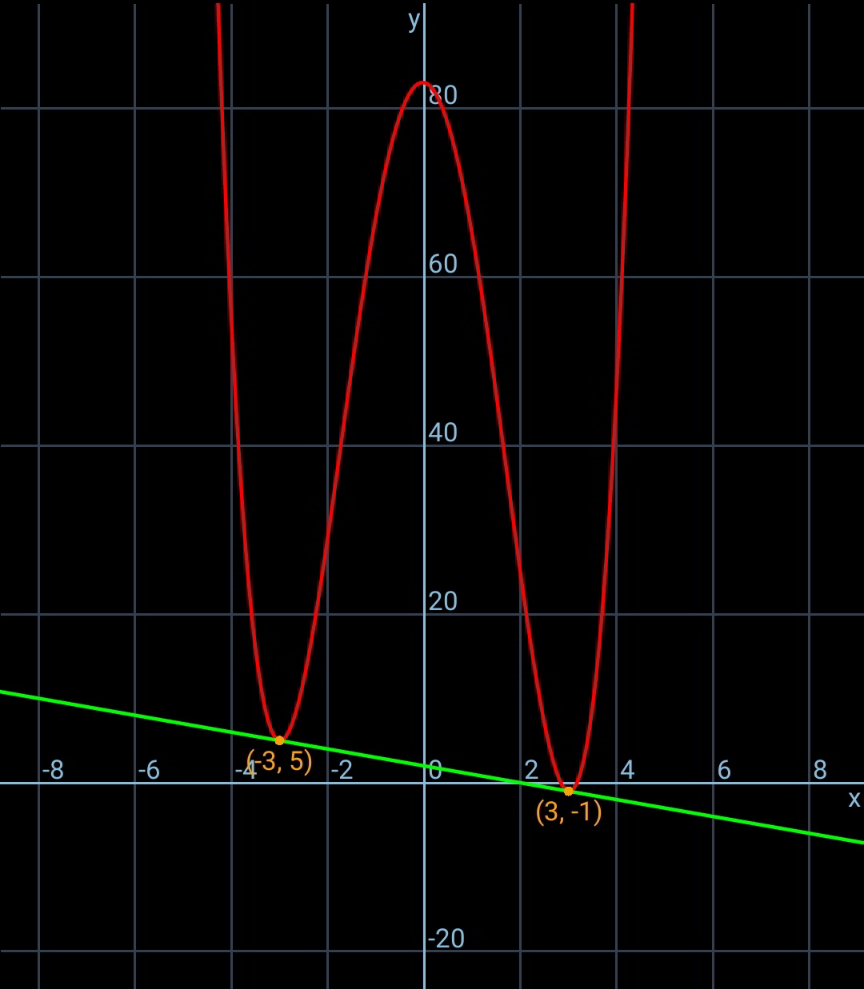
$${basically}\:{it}'{s}\:{the}\:{same}\:{solution}\:{as} \\ $$$${that}\:{from}\:{MJS}\:{sir},\:{i}\:{just}\:{put}\:{some}\: \\ $$$${more}\:{explanation}. \\ $$
Commented by Tawa11 last updated on 02/Jan/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *