Question Number 162894 by mathacek last updated on 02/Jan/22

Answered by Ar Brandon last updated on 02/Jan/22
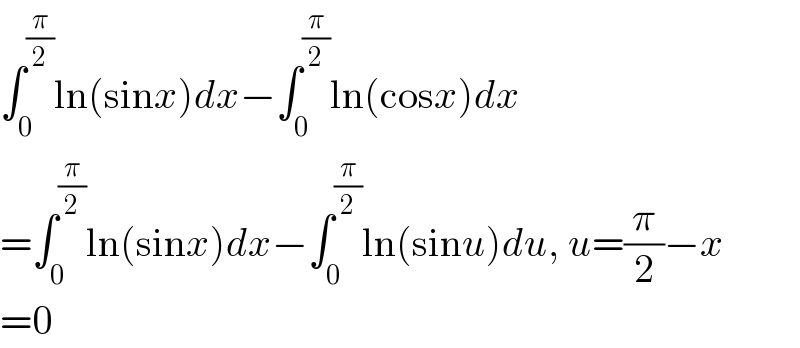
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{cos}{x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{x}\right){dx}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{sin}{u}\right){du},\:{u}=\frac{\pi}{\mathrm{2}}−{x} \\ $$$$=\mathrm{0} \\ $$
Commented by mathacek last updated on 02/Jan/22

$${Nice}! \\ $$
