Question Number 162946 by HongKing last updated on 02/Jan/22
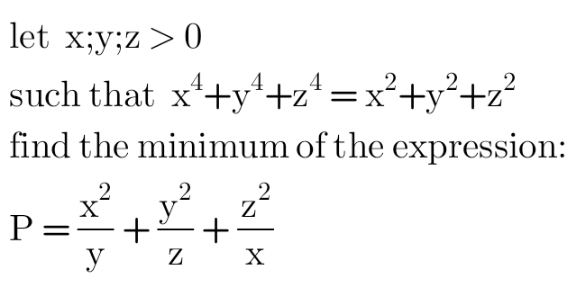
Answered by ajfour last updated on 02/Jan/22
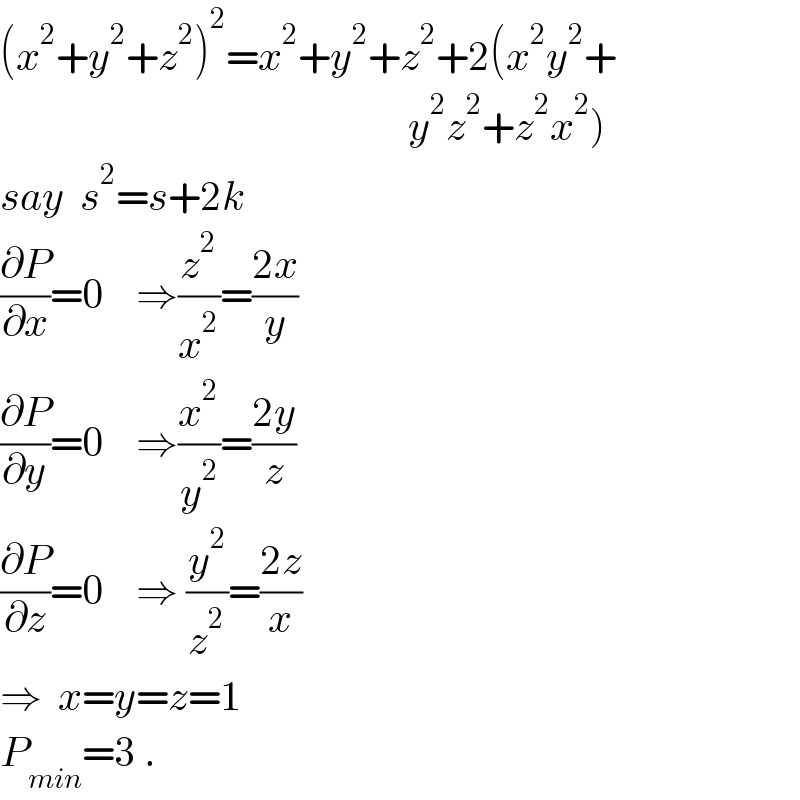
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{2}\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} +\right. \\ $$$$\left.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{y}^{\mathrm{2}} {z}^{\mathrm{2}} +{z}^{\mathrm{2}} {x}^{\mathrm{2}} \right) \\ $$$${say}\:\:{s}^{\mathrm{2}} ={s}+\mathrm{2}{k} \\ $$$$\frac{\partial{P}}{\partial{x}}=\mathrm{0}\:\:\:\:\Rightarrow\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} }=\frac{\mathrm{2}{x}}{{y}} \\ $$$$\frac{\partial{P}}{\partial{y}}=\mathrm{0}\:\:\:\:\Rightarrow\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }=\frac{\mathrm{2}{y}}{{z}} \\ $$$$\frac{\partial{P}}{\partial{z}}=\mathrm{0}\:\:\:\:\Rightarrow\:\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} }=\frac{\mathrm{2}{z}}{{x}} \\ $$$$\Rightarrow\:\:{x}={y}={z}=\mathrm{1} \\ $$$${P}_{{min}} =\mathrm{3}\:. \\ $$
