Question Number 163048 by mnjuly1970 last updated on 03/Jan/22

Answered by mahdipoor last updated on 03/Jan/22
![sin^2 x=m cos^2 x=n ⇒m^′ =−n^′ =2cosx.sinx f ′=(nm^3 +mn^3 ) ′=m′(3nm^2 +n^3 )+n′(3mn^2 +m^3 )= 2cosx.sinx(n^3 −3mn^2 +3m^2 n−m^3 )= sin2x(n−m)^3 = sin2x(cos^2 x−sin^2 x)^3 = sin2x.cos^3 2x=0 ⇒x=((kπ)/4)+(π/2) { ((sin(((kπ)/4)+(π/2))=cos(((kπ)/4)))),((cos(((kπ)/4)+(π/2))=−sin(((kπ)/2)))) :} f(((kπ)/4)+(π/2))=(1/4)sin^2 (((kπ)/2))(sin^4 (((kπ)/4))+cos^4 (((kπ)/4))) = { ((2∣k f=0)),((2∤k f=+(1/8))) :} R_f =[0,0.125]](https://www.tinkutara.com/question/Q163055.png)
$${sin}^{\mathrm{2}} {x}={m}\:\:\:{cos}^{\mathrm{2}} {x}={n} \\ $$$$\Rightarrow{m}^{'} =−{n}^{'} =\mathrm{2}{cosx}.{sinx} \\ $$$$\:{f}\:'=\left({nm}^{\mathrm{3}} +{mn}^{\mathrm{3}} \right)\:'={m}'\left(\mathrm{3}{nm}^{\mathrm{2}} +{n}^{\mathrm{3}} \right)+{n}'\left(\mathrm{3}{mn}^{\mathrm{2}} +{m}^{\mathrm{3}} \right)= \\ $$$$\mathrm{2}{cosx}.{sinx}\left({n}^{\mathrm{3}} −\mathrm{3}{mn}^{\mathrm{2}} +\mathrm{3}{m}^{\mathrm{2}} {n}−{m}^{\mathrm{3}} \right)= \\ $$$${sin}\mathrm{2}{x}\left({n}−{m}\right)^{\mathrm{3}} = \\ $$$${sin}\mathrm{2}{x}\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} = \\ $$$${sin}\mathrm{2}{x}.{cos}^{\mathrm{3}} \mathrm{2}{x}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}} \\ $$$$\begin{cases}{{sin}\left(\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}\right)={cos}\left(\frac{{k}\pi}{\mathrm{4}}\right)}\\{{cos}\left(\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}\right)=−{sin}\left(\frac{{k}\pi}{\mathrm{2}}\right)}\end{cases}\: \\ $$$${f}\left(\frac{{k}\pi}{\mathrm{4}}+\frac{\pi}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{4}}{sin}^{\mathrm{2}} \left(\frac{{k}\pi}{\mathrm{2}}\right)\left({sin}^{\mathrm{4}} \left(\frac{{k}\pi}{\mathrm{4}}\right)+{cos}^{\mathrm{4}} \left(\frac{{k}\pi}{\mathrm{4}}\right)\right) \\ $$$$=\begin{cases}{\mathrm{2}\mid{k}\:\:{f}=\mathrm{0}}\\{\mathrm{2}\nmid{k}\:\:{f}=+\frac{\mathrm{1}}{\mathrm{8}}}\end{cases} \\ $$$${R}_{{f}} =\left[\mathrm{0},\mathrm{0}.\mathrm{125}\right] \\ $$
Commented by mnjuly1970 last updated on 03/Jan/22
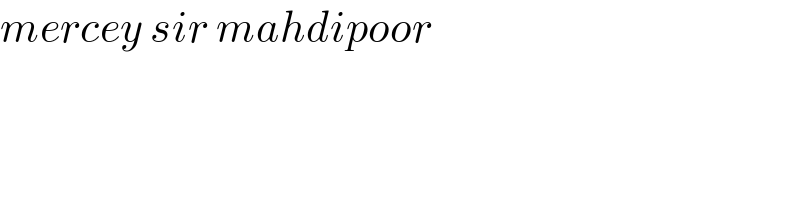
$${mercey}\:{sir}\:{mahdipoor} \\ $$
Answered by tounghoungko last updated on 03/Jan/22
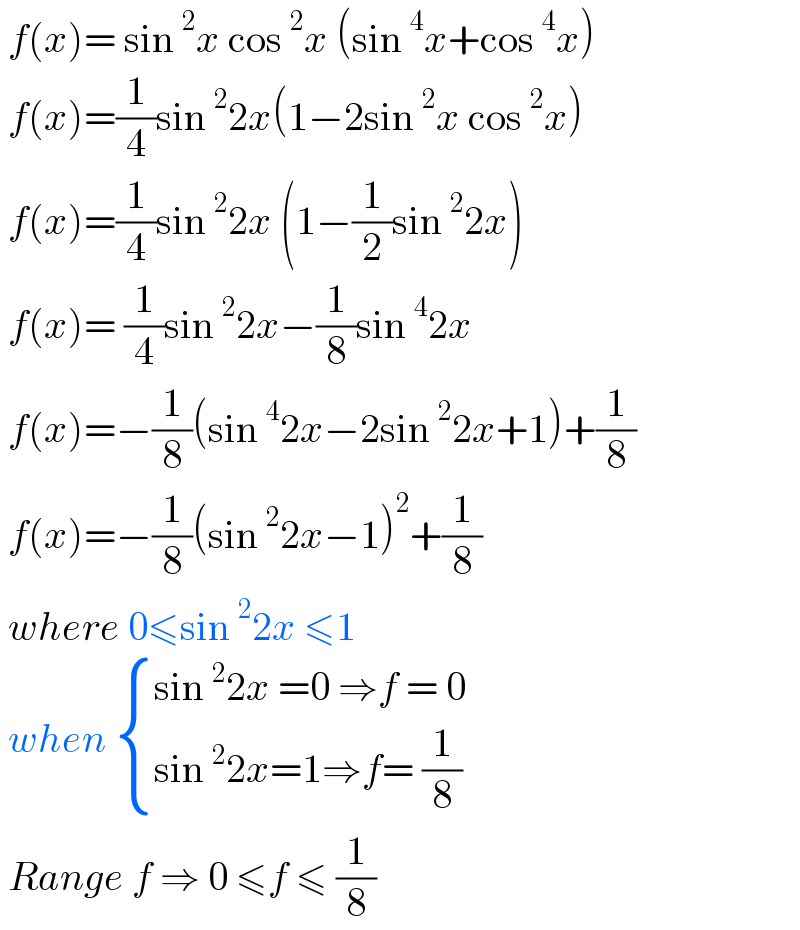
$$\:{f}\left({x}\right)=\:\mathrm{sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}\:\left(\mathrm{sin}\:^{\mathrm{4}} {x}+\mathrm{cos}\:^{\mathrm{4}} {x}\right) \\ $$$$\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} {x}\:\mathrm{cos}\:^{\mathrm{2}} {x}\right) \\ $$$$\:{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\right) \\ $$$$\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}−\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}{x}\: \\ $$$$\:{f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{sin}\:^{\mathrm{4}} \mathrm{2}{x}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{2}{x}+\mathrm{1}\right)+\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\:{f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}−\mathrm{1}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\:{where}\:\mathrm{0}\leqslant\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\:\leqslant\mathrm{1} \\ $$$$\:{when}\:\begin{cases}{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}\:=\mathrm{0}\:\Rightarrow{f}\:=\:\mathrm{0}}\\{\mathrm{sin}\:^{\mathrm{2}} \mathrm{2}{x}=\mathrm{1}\Rightarrow{f}=\:\frac{\mathrm{1}}{\mathrm{8}}}\end{cases} \\ $$$$\:{Range}\:{f}\:\Rightarrow\:\mathrm{0}\:\leqslant{f}\:\leqslant\:\frac{\mathrm{1}}{\mathrm{8}}\: \\ $$
Commented by mnjuly1970 last updated on 03/Jan/22
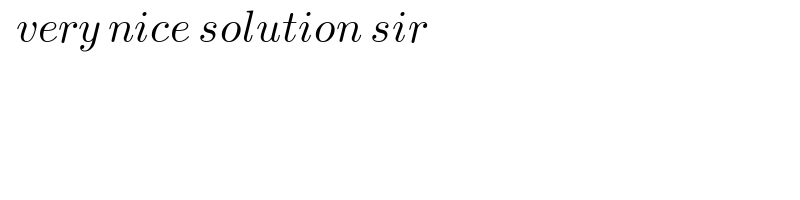
$$\:\:{very}\:{nice}\:{solution}\:{sir} \\ $$
Answered by abdullahhhhh last updated on 03/Jan/22

Commented by mnjuly1970 last updated on 03/Jan/22
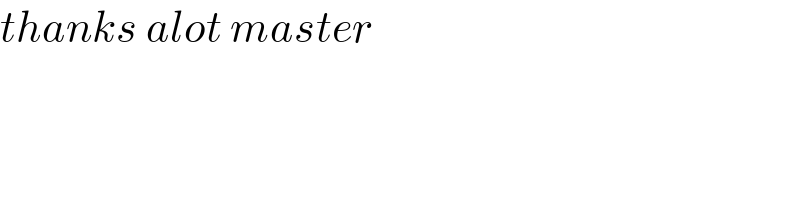
$${thanks}\:{alot}\:{master} \\ $$$$ \\ $$
