Menu Close

Question-163120

Tinku Tara 0 Comments
Pin




Question Number 163120 by ZiYangLee last updated on 04/Jan/22
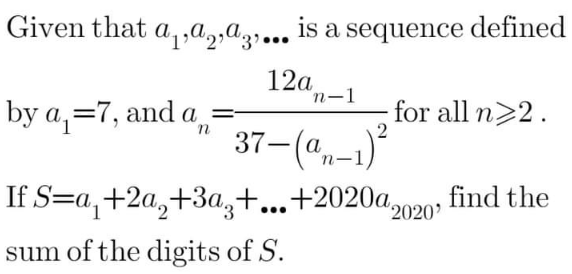
Answered by Rasheed.Sindhi last updated on 04/Jan/22
a_1 =7, a_n =((12a_(n−1) )/(37−(a_(n−1) )^2 )) for n≥2 S=a_1 +2a_2 +3a_3 +∙∙∙+2020a_(2020) Sum odigits of S=? ⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣⌢⌣ a_1 =7 a_2 =((12a_1 )/(37−(a_1 )^2 ))=((12∙7)/(37−7^2 ))=−7 a_3 =((12a_2 )/(37−(a_2 )^2 ))=((12(−7))/(37−(−7)^2 ))=7 determinant (((n∈O : a_n =7_( n∈E: a_n =−7^() ) ))) S=a_1 +2a_2 +3a_3 +∙∙∙+2020a_(2020) =7+2(−7)+3(7)+4(−7)+...+2019(7)+2020(−7) =7(1−2+3−4+...+2019−2020) =7{(1+3+5+...+2019)−(2+4+6+...+2020)} =7{((1010)/2)(1+2019)−((1010)/2)(2+2020)} =7∙505(2020−2022)=−7∙505∙2 =−7070 Sum of S 7+0+7+0=14
$${a}_{\mathrm{1}} =\mathrm{7},\:{a}_{{n}} =\frac{\mathrm{12}{a}_{{n}−\mathrm{1}} }{\mathrm{37}−\left({a}_{{n}−\mathrm{1}} \right)^{\mathrm{2}} }\:{for}\:{n}\geqslant\mathrm{2} \\ $$$${S}={a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} +\mathrm{3}{a}_{\mathrm{3}} +\centerdot\centerdot\centerdot+\mathrm{2020}{a}_{\mathrm{2020}} \\ $$$${Sum}\:{odigits}\:{of}\:{S}=? \\ $$$$\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile\frown\smile \\ $$$${a}_{\mathrm{1}} =\mathrm{7} \\ $$$${a}_{\mathrm{2}} =\frac{\mathrm{12}{a}_{\mathrm{1}} }{\mathrm{37}−\left({a}_{\mathrm{1}} \right)^{\mathrm{2}} }=\frac{\mathrm{12}\centerdot\mathrm{7}}{\mathrm{37}−\mathrm{7}^{\mathrm{2}} }=−\mathrm{7} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{12}{a}_{\mathrm{2}} }{\mathrm{37}−\left({a}_{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{12}\left(−\mathrm{7}\right)}{\mathrm{37}−\left(−\mathrm{7}\right)^{\mathrm{2}} }=\mathrm{7} \\ $$$$\begin{array}{|c|}{\underset{\:\:\:\:\:\:\:\:\:\overset{} {{n}\in\mathbb{E}:\:{a}_{{n}} =−\mathrm{7}}} {{n}\in\mathbb{O}\::\:{a}_{{n}} =\mathrm{7}}}\\\hline\end{array}\: \\ $$$${S}={a}_{\mathrm{1}} +\mathrm{2}{a}_{\mathrm{2}} +\mathrm{3}{a}_{\mathrm{3}} +\centerdot\centerdot\centerdot+\mathrm{2020}{a}_{\mathrm{2020}} \\ $$$$\:\:\:\:=\mathrm{7}+\mathrm{2}\left(−\mathrm{7}\right)+\mathrm{3}\left(\mathrm{7}\right)+\mathrm{4}\left(−\mathrm{7}\right)+…+\mathrm{2019}\left(\mathrm{7}\right)+\mathrm{2020}\left(−\mathrm{7}\right) \\ $$$$=\mathrm{7}\left(\mathrm{1}−\mathrm{2}+\mathrm{3}−\mathrm{4}+…+\mathrm{2019}−\mathrm{2020}\right) \\ $$$$=\mathrm{7}\left\{\left(\mathrm{1}+\mathrm{3}+\mathrm{5}+…+\mathrm{2019}\right)−\left(\mathrm{2}+\mathrm{4}+\mathrm{6}+…+\mathrm{2020}\right)\right\} \\ $$$$=\mathrm{7}\left\{\frac{\mathrm{1010}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2019}\right)−\frac{\mathrm{1010}}{\mathrm{2}}\left(\mathrm{2}+\mathrm{2020}\right)\right\} \\ $$$$=\mathrm{7}\centerdot\mathrm{505}\left(\mathrm{2020}−\mathrm{2022}\right)=−\mathrm{7}\centerdot\mathrm{505}\centerdot\mathrm{2} \\ $$$$=−\mathrm{7070} \\ $$$${Sum}\:{of}\:{S}\:\:\mathrm{7}+\mathrm{0}+\mathrm{7}+\mathrm{0}=\mathrm{14} \\ $$
Commented by Tawa11 last updated on 04/Jan/22
Great sir.
$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by Rasheed.Sindhi last updated on 04/Jan/22
THANX MISS!
$$\mathcal{THANX}\:\:\mathcal{MISS}! \\ $$
Commented by mr W last updated on 04/Jan/22
nice!
$${nice}! \\ $$
Commented by Rasheed.Sindhi last updated on 04/Jan/22
THANKS SIR!
$$\mathcal{THANKS}\:\:\mathcal{SIR}! \\ $$
Commented by mr W last updated on 04/Jan/22
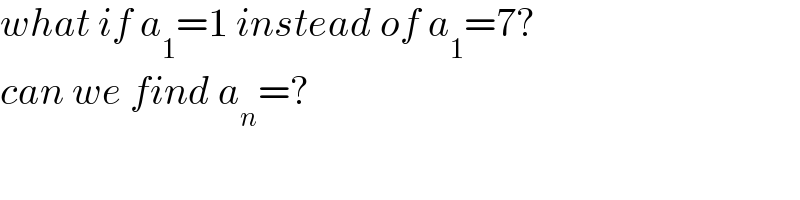
what if a_1 =1 instead of a_1 =7? can we find a_n =?
$${what}\:{if}\:{a}_{\mathrm{1}} =\mathrm{1}\:{instead}\:{of}\:{a}_{\mathrm{1}} =\mathrm{7}? \\ $$$${can}\:{we}\:{find}\:{a}_{{n}} =? \\ $$
Commented by Rasheed.Sindhi last updated on 05/Jan/22
a_1 =1 ; a_n =((12a_(n−1) )/(37−(a_(n−1) )^2 )) a_2 =((12.1)/(37−(1)^2 ))=(1/3) a_3 =((12.(1/3))/(37−((1/3))^2 ))=(4/((333−1)/9))=4.(9/(332))=(9/(83)) a_4 =((12.(9/(83)))/(37−((81)/(6889))))=.... Sir this is not so easy.I think we must first solve the given recurrence relation and obtain an expression for a_n in terms of n.I′ll try but not much confident! begin:Thanks ; goto begin
$${a}_{\mathrm{1}} =\mathrm{1}\:;\:{a}_{{n}} =\frac{\mathrm{12}{a}_{{n}−\mathrm{1}} }{\mathrm{37}−\left({a}_{{n}−\mathrm{1}} \right)^{\mathrm{2}} } \\ $$$${a}_{\mathrm{2}} =\frac{\mathrm{12}.\mathrm{1}}{\mathrm{37}−\left(\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${a}_{\mathrm{3}} =\frac{\mathrm{12}.\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{37}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\frac{\mathrm{333}−\mathrm{1}}{\mathrm{9}}}=\mathrm{4}.\frac{\mathrm{9}}{\mathrm{332}}=\frac{\mathrm{9}}{\mathrm{83}} \\ $$$${a}_{\mathrm{4}} =\frac{\mathrm{12}.\frac{\mathrm{9}}{\mathrm{83}}}{\mathrm{37}−\frac{\mathrm{81}}{\mathrm{6889}}}=…. \\ $$$${Sir}\:{this}\:{is}\:{not}\:{so}\:{easy}.{I}\:{think}\:{we}\:{must} \\ $$$${first}\:{solve}\:{the}\:{given}\:{recurrence} \\ $$$${relation}\:{and}\:{obtain}\:{an}\:{expression} \\ $$$${for}\:{a}_{{n}} \:{in}\:{terms}\:{of}\:{n}.{I}'{ll}\:{try}\:{but}\:{not} \\ $$$${much}\:{confident}! \\ $$$${begin}:\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:;\:\:{goto}\:{begin} \\ $$
Commented by mr W last updated on 05/Jan/22
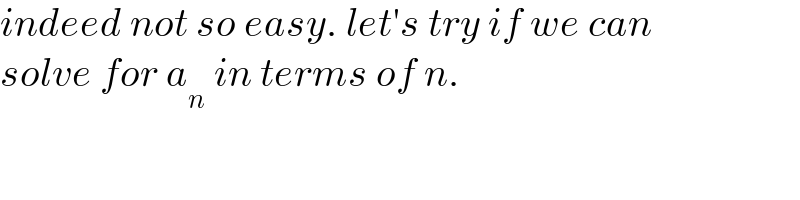
indeed not so easy. let′s try if we can solve for a_n in terms of n.
$${indeed}\:{not}\:{so}\:{easy}.\:{let}'{s}\:{try}\:{if}\:{we}\:{can} \\ $$$${solve}\:{for}\:{a}_{{n}} \:{in}\:{terms}\:{of}\:{n}. \\ $$
Commented by Rasheed.Sindhi last updated on 05/Jan/22
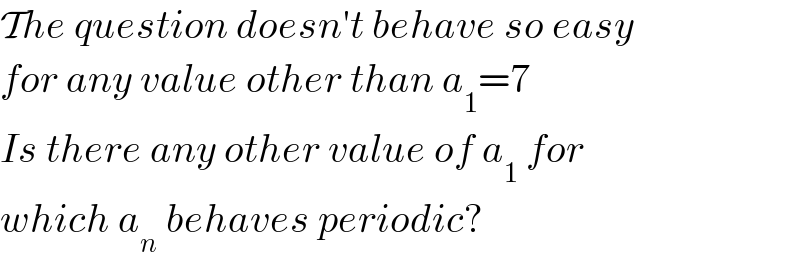
The question doesn′t behave so easy for any value other than a_1 =7 Is there any other value of a_1 for which a_n behaves periodic?
$$\mathcal{T}{he}\:{question}\:{doesn}'{t}\:{behave}\:{so}\:{easy} \\ $$$${for}\:{any}\:{value}\:{other}\:{than}\:{a}_{\mathrm{1}} =\mathrm{7} \\ $$$${Is}\:{there}\:{any}\:{other}\:{value}\:{of}\:{a}_{\mathrm{1}} \:{for} \\ $$$${which}\:{a}_{{n}} \:{behaves}\:{periodic}? \\ $$
Commented by mr W last updated on 05/Jan/22
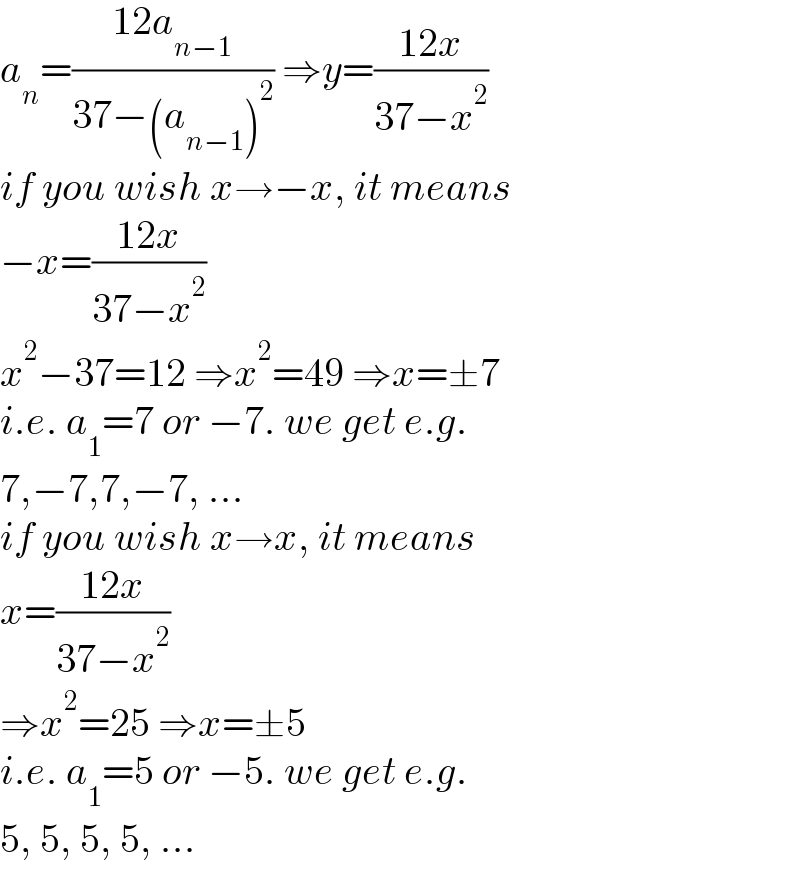
a_n =((12a_(n−1) )/(37−(a_(n−1) )^2 )) ⇒y=((12x)/(37−x^2 )) if you wish x→−x, it means −x=((12x)/(37−x^2 )) x^2 −37=12 ⇒x^2 =49 ⇒x=±7 i.e. a_1 =7 or −7. we get e.g. 7,−7,7,−7, ... if you wish x→x, it means x=((12x)/(37−x^2 )) ⇒x^2 =25 ⇒x=±5 i.e. a_1 =5 or −5. we get e.g. 5, 5, 5, 5, ...
$${a}_{{n}} =\frac{\mathrm{12}{a}_{{n}−\mathrm{1}} }{\mathrm{37}−\left({a}_{{n}−\mathrm{1}} \right)^{\mathrm{2}} }\:\Rightarrow{y}=\frac{\mathrm{12}{x}}{\mathrm{37}−{x}^{\mathrm{2}} } \\ $$$${if}\:{you}\:{wish}\:{x}\rightarrow−{x},\:{it}\:{means} \\ $$$$−{x}=\frac{\mathrm{12}{x}}{\mathrm{37}−{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{2}} −\mathrm{37}=\mathrm{12}\:\Rightarrow{x}^{\mathrm{2}} =\mathrm{49}\:\Rightarrow{x}=\pm\mathrm{7} \\ $$$${i}.{e}.\:{a}_{\mathrm{1}} =\mathrm{7}\:{or}\:−\mathrm{7}.\:{we}\:{get}\:{e}.{g}. \\ $$$$\mathrm{7},−\mathrm{7},\mathrm{7},−\mathrm{7},\:… \\ $$$${if}\:{you}\:{wish}\:{x}\rightarrow{x},\:{it}\:{means} \\ $$$${x}=\frac{\mathrm{12}{x}}{\mathrm{37}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{25}\:\Rightarrow{x}=\pm\mathrm{5} \\ $$$${i}.{e}.\:{a}_{\mathrm{1}} =\mathrm{5}\:{or}\:−\mathrm{5}.\:{we}\:{get}\:{e}.{g}. \\ $$$$\mathrm{5},\:\mathrm{5},\:\mathrm{5},\:\mathrm{5},\:… \\ $$
Commented by Rasheed.Sindhi last updated on 05/Jan/22
Sir, you′re deep in maths and hence particularly in this question also! Thanks from my deep heart!
$$\mathbb{S}\mathrm{ir},\:\mathrm{you}'\mathrm{re}\:\mathrm{deep}\:\mathrm{in}\:\mathrm{maths}\:\mathrm{and}\:\mathrm{hence} \\ $$$$\mathrm{particularly}\:\mathrm{in}\:\mathrm{this}\:\mathrm{question}\:\mathrm{also}! \\ $$$$\mathcal{T}{hanks}\:{from}\:{my}\:{deep}\:{heart}! \\ $$
Commented by mr W last updated on 05/Jan/22
thanks!
$${thanks}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *