Question Number 163210 by HongKing last updated on 04/Jan/22

Commented by amin96 last updated on 05/Jan/22
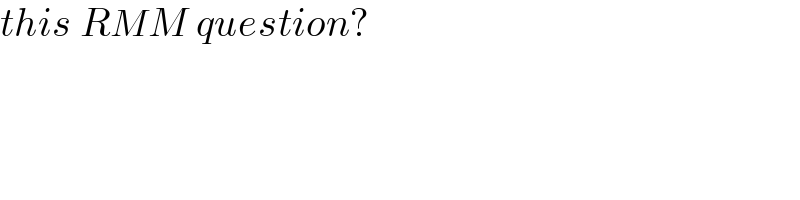
$${this}\:{RMM}\:{question}? \\ $$
Answered by mr W last updated on 05/Jan/22

Commented by mr W last updated on 05/Jan/22
![say the side lengthes of the three equilateral triangles are a,b,c respectively. a=b+c from Q163100 we know ΔIJK is also an equilateral with side length s=(√((b^2 +c^2 +bc)/3)) it′s easy to get that JO⊥DE, DK⊥DE. therefore JO//DK. similarly we get DJ//KO. ⇒JO=DK=(2/3)×(((√3)c)/2)=(((√3)c)/3) ⇒KO=DJ=(2/3)×(((√3)b)/2)=(((√3)b)/3) ∠JOK=∠JDK=120° [JOK]=((JO×KO×sin ∠JOK)/2) =(1/2)×(((√3)c)/3)×(((√3)b)/3)×((√3)/2)=(((√3)bc)/(12)) [IJK]=(((√3)s^2 )/4)=(((√3)(b^2 +c^2 +bc))/(12)) [IJOK]=[IJK]+[JOK] =(((√3)(b^2 +c^2 +bc))/(12))+(((√3)bc)/(12)) =(((√3)(b+c)^2 )/(12))=(((√3)a^2 )/(12)) [ABC]=(((√3)a^2 )/4)=3×(((√3)a^2 )/(12))=3×[IJOK] ✓](https://www.tinkutara.com/question/Q163249.png)
$${say}\:{the}\:{side}\:{lengthes}\:{of}\:{the}\:{three} \\ $$$${equilateral}\:{triangles}\:{are}\:{a},{b},{c} \\ $$$${respectively}. \\ $$$${a}={b}+{c} \\ $$$${from}\:{Q}\mathrm{163100}\:{we}\:{know}\:\Delta{IJK}\:{is} \\ $$$${also}\:{an}\:{equilateral}\:{with}\:{side}\:{length} \\ $$$${s}=\sqrt{\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}}{\mathrm{3}}} \\ $$$${it}'{s}\:{easy}\:{to}\:{get}\:{that}\:{JO}\bot{DE},\:{DK}\bot{DE}. \\ $$$${therefore}\:{JO}//{DK}. \\ $$$${similarly}\:{we}\:{get}\:{DJ}//{KO}. \\ $$$$\Rightarrow{JO}={DK}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{3}} \\ $$$$\Rightarrow{KO}={DJ}=\frac{\mathrm{2}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}} \\ $$$$\angle{JOK}=\angle{JDK}=\mathrm{120}° \\ $$$$\left[{JOK}\right]=\frac{{JO}×{KO}×\mathrm{sin}\:\angle{JOK}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\sqrt{\mathrm{3}}{c}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}{b}}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}{bc}}{\mathrm{12}} \\ $$$$\left[{IJK}\right]=\frac{\sqrt{\mathrm{3}}{s}^{\mathrm{2}} }{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right)}{\mathrm{12}} \\ $$$$\left[{IJOK}\right]=\left[{IJK}\right]+\left[{JOK}\right] \\ $$$$\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{bc}\right)}{\mathrm{12}}+\frac{\sqrt{\mathrm{3}}{bc}}{\mathrm{12}} \\ $$$$\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}\left({b}+{c}\right)^{\mathrm{2}} }{\mathrm{12}}=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\left[{ABC}\right]=\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{3}×\frac{\sqrt{\mathrm{3}}{a}^{\mathrm{2}} }{\mathrm{12}}=\mathrm{3}×\left[{IJOK}\right]\:\checkmark \\ $$
Commented by Tawa11 last updated on 05/Jan/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
Commented by HongKing last updated on 05/Jan/22
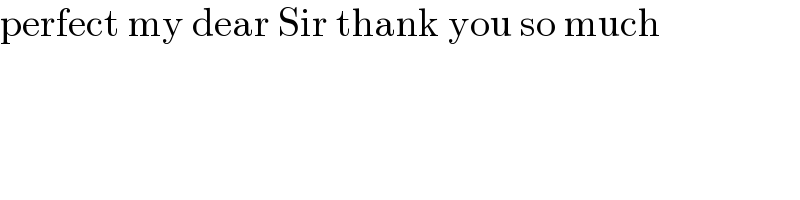
$$\mathrm{perfect}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
