Question Number 163226 by nurtani last updated on 05/Jan/22

Commented by Rasheed.Sindhi last updated on 06/Jan/22

$$\boldsymbol{\mathrm{Sir}}\:\boldsymbol{\mathrm{mr}}\:\boldsymbol{\mathrm{W}},{why}\:{have}\:{you}\:{deleted}\:{your} \\ $$$${answer}? \\ $$
Commented by mr W last updated on 06/Jan/22
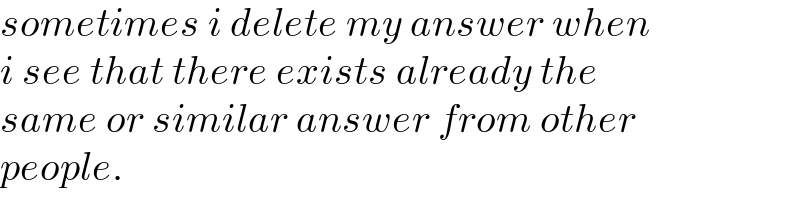
$${sometimes}\:{i}\:{delete}\:{my}\:{answer}\:{when} \\ $$$${i}\:{see}\:{that}\:{there}\:{exists}\:{already}\:{the}\: \\ $$$${same}\:{or}\:{similar}\:{answer}\:{from}\:{other} \\ $$$${people}. \\ $$
Commented by Rasheed.Sindhi last updated on 06/Jan/22

$${Understood}\:\boldsymbol{{sir}}! \\ $$
Answered by cortano1 last updated on 05/Jan/22
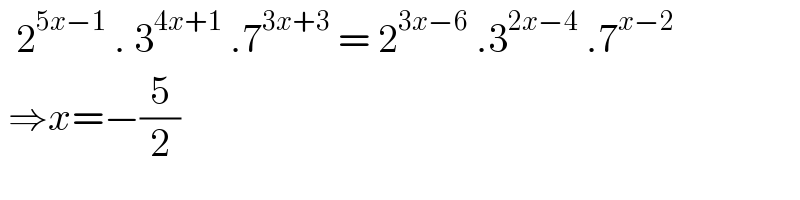
$$\:\:\mathrm{2}^{\mathrm{5}{x}−\mathrm{1}} \:.\:\mathrm{3}^{\mathrm{4}{x}+\mathrm{1}} \:.\mathrm{7}^{\mathrm{3}{x}+\mathrm{3}} \:=\:\mathrm{2}^{\mathrm{3}{x}−\mathrm{6}} \:.\mathrm{3}^{\mathrm{2}{x}−\mathrm{4}} \:.\mathrm{7}^{{x}−\mathrm{2}} \\ $$$$\:\Rightarrow{x}=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$
Answered by Rasheed.Sindhi last updated on 05/Jan/22
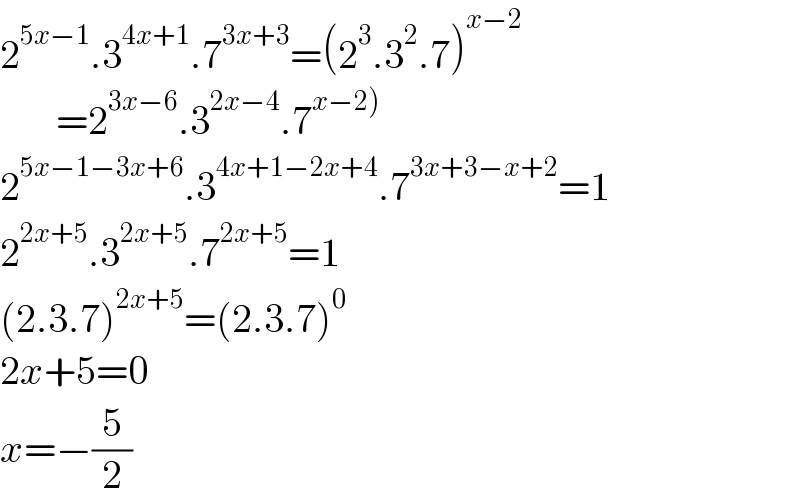
$$\mathrm{2}^{\mathrm{5}{x}−\mathrm{1}} .\mathrm{3}^{\mathrm{4}{x}+\mathrm{1}} .\mathrm{7}^{\mathrm{3}{x}+\mathrm{3}} =\left(\mathrm{2}^{\mathrm{3}} .\mathrm{3}^{\mathrm{2}} .\mathrm{7}\right)^{{x}−\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{3}{x}−\mathrm{6}} .\mathrm{3}^{\mathrm{2}{x}−\mathrm{4}} .\mathrm{7}^{\left.{x}−\mathrm{2}\right)} \\ $$$$\mathrm{2}^{\mathrm{5}{x}−\mathrm{1}−\mathrm{3}{x}+\mathrm{6}} .\mathrm{3}^{\mathrm{4}{x}+\mathrm{1}−\mathrm{2}{x}+\mathrm{4}} .\mathrm{7}^{\mathrm{3}{x}+\mathrm{3}−{x}+\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{2}{x}+\mathrm{5}} .\mathrm{3}^{\mathrm{2}{x}+\mathrm{5}} .\mathrm{7}^{\mathrm{2}{x}+\mathrm{5}} =\mathrm{1} \\ $$$$\left(\mathrm{2}.\mathrm{3}.\mathrm{7}\right)^{\mathrm{2}{x}+\mathrm{5}} =\left(\mathrm{2}.\mathrm{3}.\mathrm{7}\right)^{\mathrm{0}} \\ $$$$\mathrm{2}{x}+\mathrm{5}=\mathrm{0} \\ $$$${x}=−\frac{\mathrm{5}}{\mathrm{2}} \\ $$
