Question Number 163293 by ajfour last updated on 05/Jan/22
Commented by ajfour last updated on 05/Jan/22

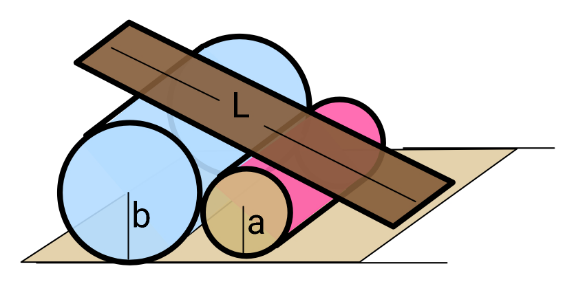
$${If}\:{the}\:{plank}\:{rests}\:{on}\:{two}\:{fixed}\:{cylinders} \\ $$$${in}\:{contact}\:{with}\:{each}\:{other}\:{and}\: \\ $$$${ground},\:{and}\:{if}\:{the}\:{bottom}\:{edge}\:{of} \\ $$$${plank}\:{is}\:{just}\:{bit}\:{above}\:{ground},{find} \\ $$$${friction}\:{coefficient}\:\mu_{{min}} \:{between} \\ $$$${plank}\:{and}\:{cylinder},\:{such}\:{that}\:{the} \\ $$$${plank}\:{can}\:{be}\:{in}\:{static}\:{equilibrium}. \\ $$
Answered by mr W last updated on 06/Jan/22
Commented by mr W last updated on 06/Jan/22
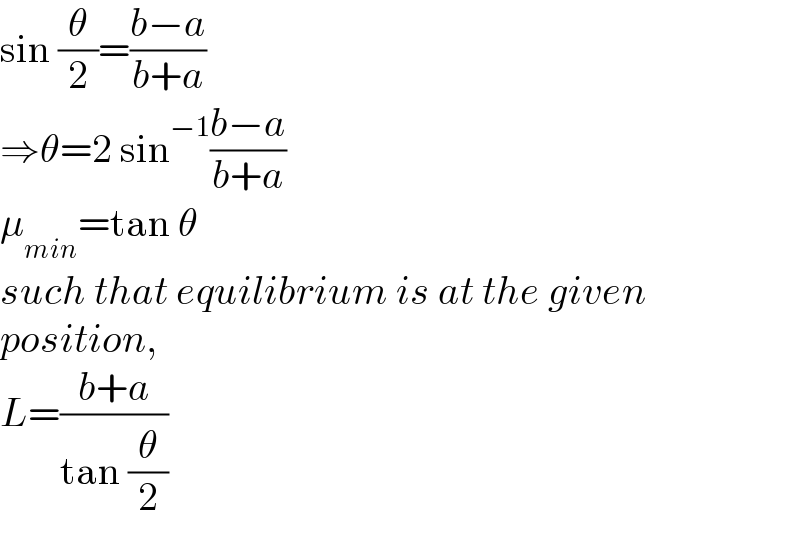
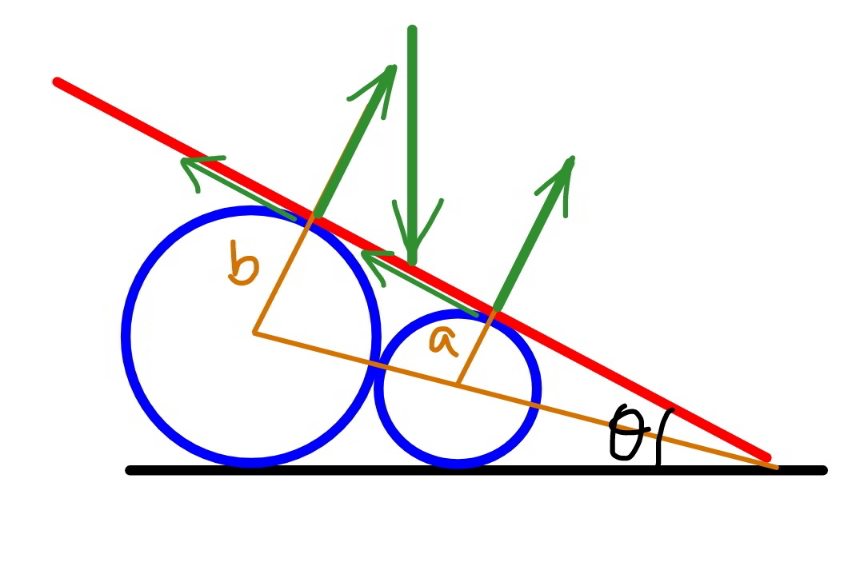
$$\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\frac{{b}−{a}}{{b}+{a}} \\ $$$$\Rightarrow\theta=\mathrm{2}\:\mathrm{sin}^{−\mathrm{1}} \frac{{b}−{a}}{{b}+{a}} \\ $$$$\mu_{{min}} =\mathrm{tan}\:\theta \\ $$$${such}\:{that}\:{equilibrium}\:{is}\:{at}\:{the}\:{given} \\ $$$${position}, \\ $$$${L}=\frac{{b}+{a}}{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}} \\ $$
Commented by ajfour last updated on 07/Jan/22
$${Thank}\:{u}\:{sir},\:{i}\:{m}\:{bit}\:{unwell}.. \\ $$
Commented by mr W last updated on 07/Jan/22

$${get}\:{well}\:{soon}\:{sir}! \\ $$
