Question Number 163367 by poeter last updated on 06/Jan/22

Answered by som(math1967) last updated on 06/Jan/22
![1. equn of circle x^2 +y^2 =10 (given) (dy/dx)=((−x)/y) [(dy/dx)]_(1,3) =((−1)/3) ∴slope of tanjent=((−1)/3) equation of tanjent (y−3)=((−1)/3)(x−1) x+3y=10](https://www.tinkutara.com/question/Q163380.png)
$$\mathrm{1}.\:{equn}\:{of}\:{circle}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{10}\:\left({given}\right) \\ $$$$\:\:\frac{{dy}}{{dx}}=\frac{−{x}}{{y}} \\ $$$$\left[\frac{{dy}}{{dx}}\right]_{\mathrm{1},\mathrm{3}} =\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$$\therefore{slope}\:{of}\:{tanjent}=\frac{−\mathrm{1}}{\mathrm{3}} \\ $$$${equation}\:{of}\:{tanjent} \\ $$$$\:\:\left({y}−\mathrm{3}\right)=\frac{−\mathrm{1}}{\mathrm{3}}\left({x}−\mathrm{1}\right) \\ $$$$\:{x}+\mathrm{3}{y}=\mathrm{10} \\ $$
Answered by MikeH last updated on 06/Jan/22
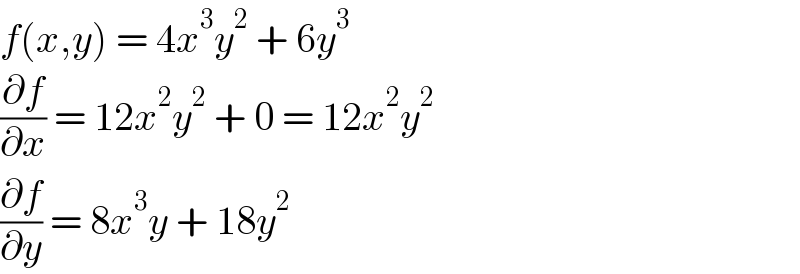
$${f}\left({x},{y}\right)\:=\:\mathrm{4}{x}^{\mathrm{3}} {y}^{\mathrm{2}} \:+\:\mathrm{6}{y}^{\mathrm{3}} \\ $$$$\frac{\partial{f}}{\partial{x}}\:=\:\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:+\:\mathrm{0}\:=\:\mathrm{12}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \\ $$$$\frac{\partial{f}}{\partial{y}}\:=\:\mathrm{8}{x}^{\mathrm{3}} {y}\:+\:\mathrm{18}{y}^{\mathrm{2}} \\ $$
