Question Number 16338 by ajfour last updated on 20/Jun/17
Commented by mrW1 last updated on 20/Jun/17
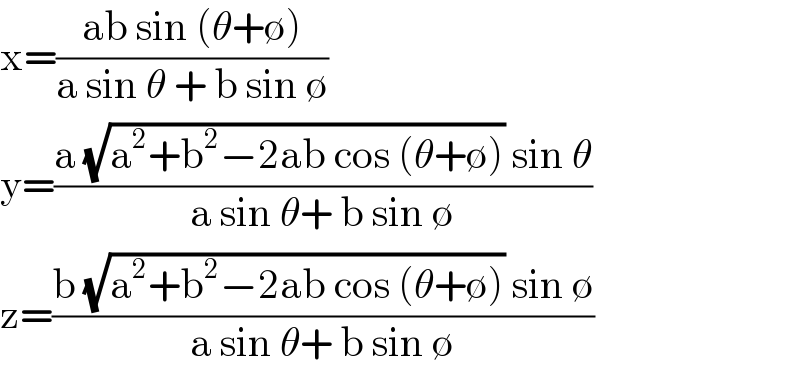
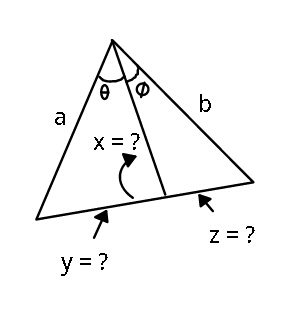
$$\mathrm{x}=\frac{\mathrm{ab}\:\mathrm{sin}\:\left(\theta+\emptyset\right)}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\emptyset} \\ $$$$\mathrm{y}=\frac{\mathrm{a}\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\left(\theta+\emptyset\right)}\:\mathrm{sin}\:\theta}{\mathrm{a}\:\mathrm{sin}\:\theta+\:\mathrm{b}\:\mathrm{sin}\:\emptyset} \\ $$$$\mathrm{z}=\frac{\mathrm{b}\:\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\left(\theta+\emptyset\right)}\:\mathrm{sin}\:\emptyset}{\mathrm{a}\:\mathrm{sin}\:\theta+\:\mathrm{b}\:\mathrm{sin}\:\emptyset} \\ $$
Commented by ajfour last updated on 20/Jun/17
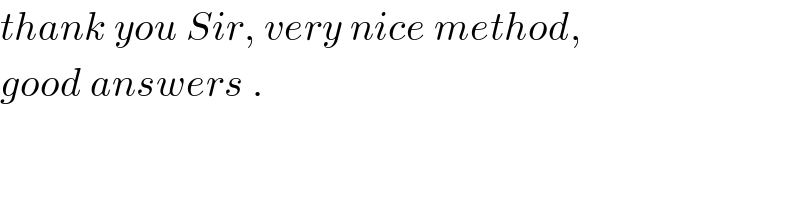
$${thank}\:{you}\:{Sir},\:{very}\:{nice}\:{method}, \\ $$$${good}\:{answers}\:. \\ $$
Answered by mrW1 last updated on 20/Jun/17
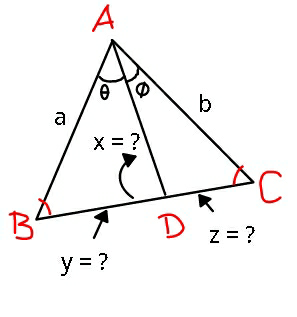
![((BC)/(sin (θ+φ)))=(a/(sin C))=(b/(sin B)) (x/(sin B))=(y/(sin θ)) ⇒y=xsin θ(1/(sin B))=xsin θ((BC)/(bsin (θ+φ))) (x/(sin C))=(z/(sin φ)) ⇒z=xsin φ(1/(sin C))=xsin φ((BC)/(asin (θ+φ))) BC=y+z=x((BC)/(sin (θ+φ)))[((sin θ)/b)+((sin φ)/a)] 1=(x/(sin (θ+φ)))[((sin θ)/b)+((sin φ)/a)] ⇒x=((ab sin (θ+φ))/(a sin θ + b sin φ)) BC=(√(a^2 +b^2 −2ab cos (θ+φ))) y=((x sin θ)/(b sin (θ+φ)))×BC =((ab sin (θ+φ))/(a sin θ + b sin φ))×((sin θ)/(b sin (θ+φ)))×BC =((a sin θ)/(a sin θ + b sin φ))×BC ⇒y=((a sin θ)/(a sin θ + b sin φ))×(√(a^2 +b^2 −2ab cos (θ+φ))) similarly ⇒z=((b sin φ)/(a sin θ + b sin φ))×(√(a^2 +b^2 −2ab cos (θ+φ)))](https://www.tinkutara.com/question/Q16343.png)
$$\frac{\mathrm{BC}}{\mathrm{sin}\:\left(\theta+\phi\right)}=\frac{\mathrm{a}}{\mathrm{sin}\:\mathrm{C}}=\frac{\mathrm{b}}{\mathrm{sin}\:\mathrm{B}} \\ $$$$ \\ $$$$\frac{\mathrm{x}}{\mathrm{sin}\:\mathrm{B}}=\frac{\mathrm{y}}{\mathrm{sin}\:\theta} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{xsin}\:\theta\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{B}}=\mathrm{xsin}\:\theta\frac{\mathrm{BC}}{\mathrm{bsin}\:\left(\theta+\phi\right)} \\ $$$$\frac{\mathrm{x}}{\mathrm{sin}\:\mathrm{C}}=\frac{\mathrm{z}}{\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\mathrm{z}=\mathrm{xsin}\:\phi\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{C}}=\mathrm{xsin}\:\phi\frac{\mathrm{BC}}{\mathrm{asin}\:\left(\theta+\phi\right)} \\ $$$$ \\ $$$$\mathrm{BC}=\mathrm{y}+\mathrm{z}=\mathrm{x}\frac{\mathrm{BC}}{\mathrm{sin}\:\left(\theta+\phi\right)}\left[\frac{\mathrm{sin}\:\theta}{\mathrm{b}}+\frac{\mathrm{sin}\:\phi}{\mathrm{a}}\right] \\ $$$$\mathrm{1}=\frac{\mathrm{x}}{\mathrm{sin}\:\left(\theta+\phi\right)}\left[\frac{\mathrm{sin}\:\theta}{\mathrm{b}}+\frac{\mathrm{sin}\:\phi}{\mathrm{a}}\right] \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{ab}\:\mathrm{sin}\:\left(\theta+\phi\right)}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\phi} \\ $$$$ \\ $$$$\mathrm{BC}=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$$ \\ $$$$\mathrm{y}=\frac{\mathrm{x}\:\mathrm{sin}\:\theta}{\mathrm{b}\:\mathrm{sin}\:\left(\theta+\phi\right)}×\mathrm{BC} \\ $$$$=\frac{\mathrm{ab}\:\mathrm{sin}\:\left(\theta+\phi\right)}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\phi}×\frac{\mathrm{sin}\:\theta}{\mathrm{b}\:\mathrm{sin}\:\left(\theta+\phi\right)}×\mathrm{BC} \\ $$$$=\frac{\mathrm{a}\:\mathrm{sin}\:\theta}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\phi}×\mathrm{BC} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{a}\:\mathrm{sin}\:\theta}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\phi}×\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$$$\mathrm{similarly} \\ $$$$\Rightarrow\mathrm{z}=\frac{\mathrm{b}\:\mathrm{sin}\:\phi}{\mathrm{a}\:\mathrm{sin}\:\theta\:+\:\mathrm{b}\:\mathrm{sin}\:\phi}×\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} −\mathrm{2ab}\:\mathrm{cos}\:\left(\theta+\phi\right)} \\ $$
Commented by mrW1 last updated on 20/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 20/Jun/17

$${perfect}! \\ $$
Commented by ajfour last updated on 20/Jun/17
$${great}\:{sir},\:{i}\:{believe}\:{these}\:{are} \\ $$$${useful}\:{answers}. \\ $$
