Question-163384

Question Number 163384 by amin96 last updated on 06/Jan/22

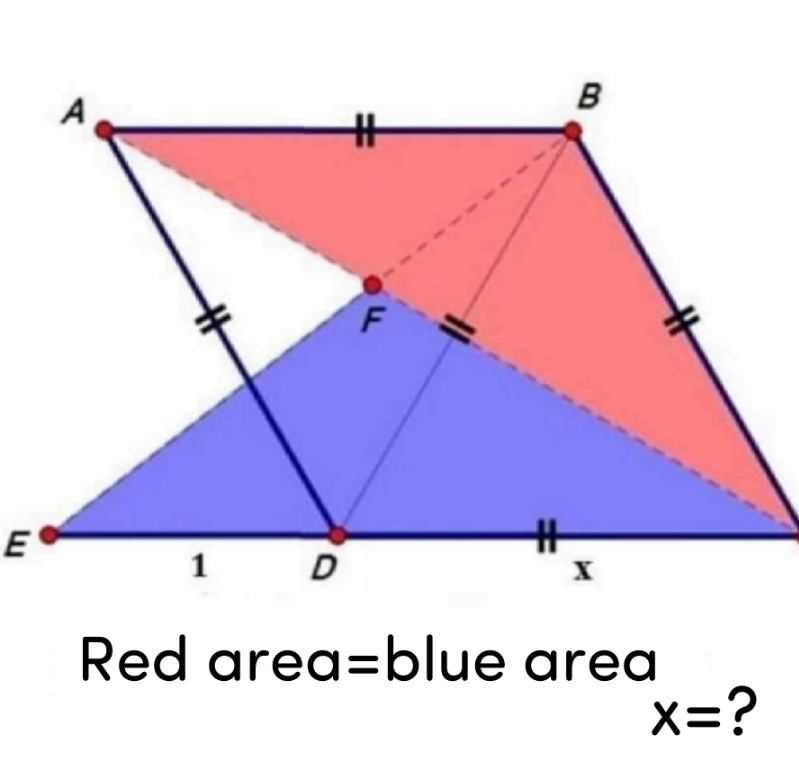
Answered by mr W last updated on 06/Jan/22

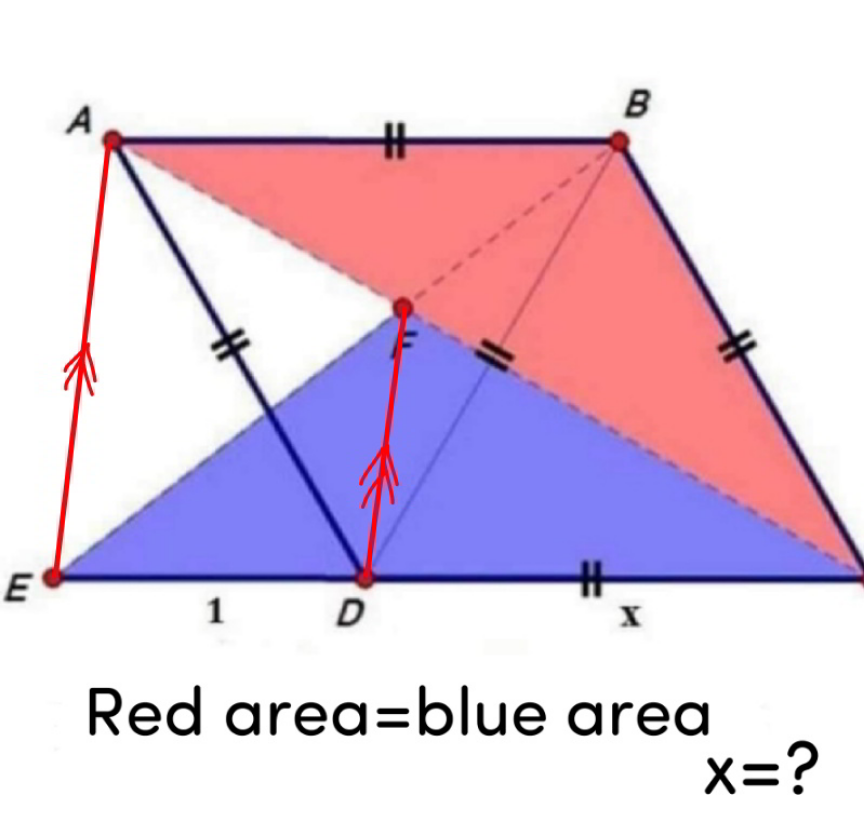
Commented by mr W last updated on 06/Jan/22

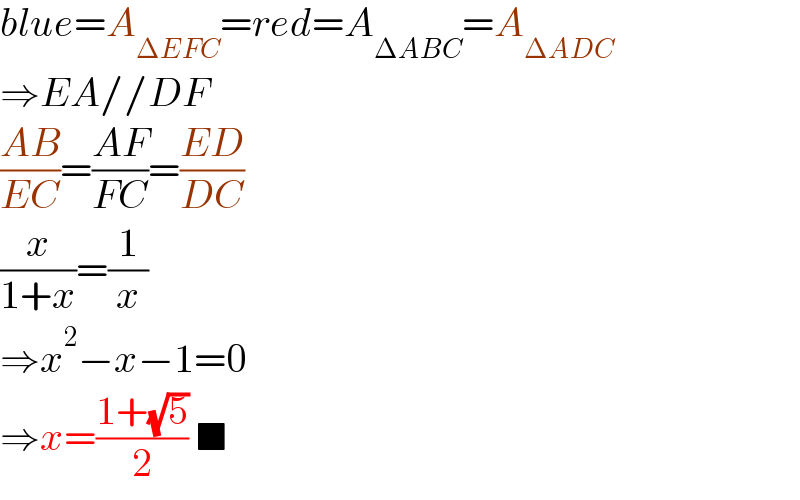
blue=A_(ΔEFC) =red=A_(ΔABC) =A_(ΔADC) ⇒EA//DF ((AB)/(EC))=((AF)/(FC))=((ED)/(DC)) (x/(1+x))=(1/x) ⇒x^2 −x−1=0 ⇒x=((1+(√5))/2) ■

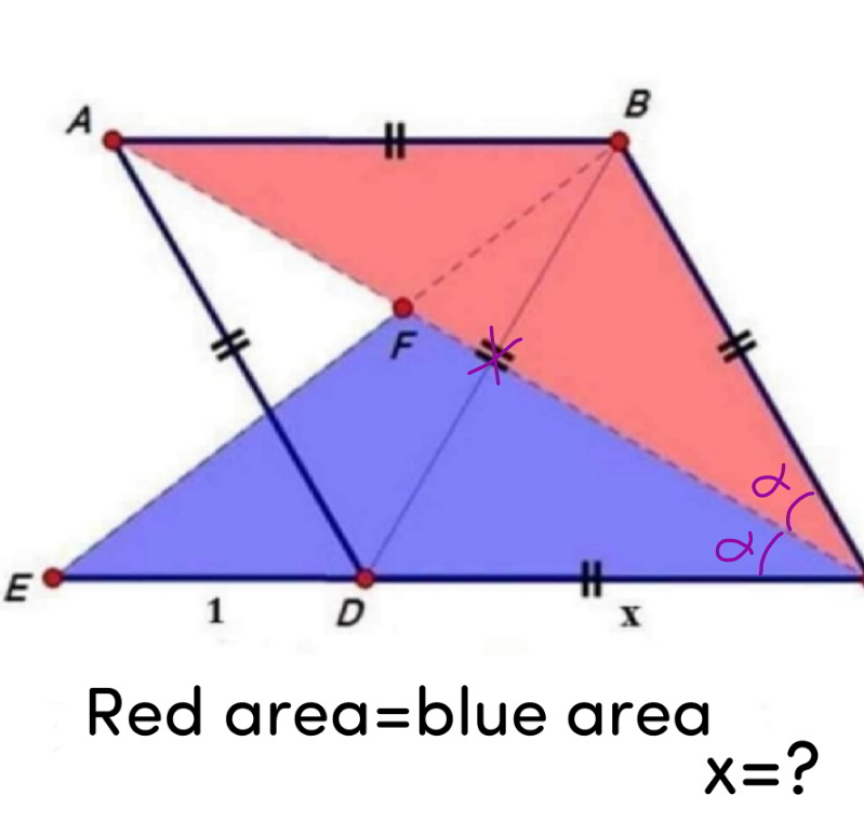
$${blue}={A}_{\Delta{EFC}} ={red}={A}_{\Delta{ABC}} ={A}_{\Delta{ADC}} \\ $$$$\Rightarrow{EA}//{DF} \\ $$$$\frac{{AB}}{{EC}}=\frac{{AF}}{{FC}}=\frac{{ED}}{{DC}} \\ $$$$\frac{{x}}{\mathrm{1}+{x}}=\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\blacksquare \\ $$

Commented by amin96 last updated on 06/Jan/22

$${yes}\:{sir}.\:{thanks}\:{mr}\:{W} \\ $$

Commented by amin96 last updated on 06/Jan/22

$$ \\ $$Could you please tell me why is DF parallel to AE?

Commented by mr W last updated on 06/Jan/22

Commented by mr W last updated on 06/Jan/22

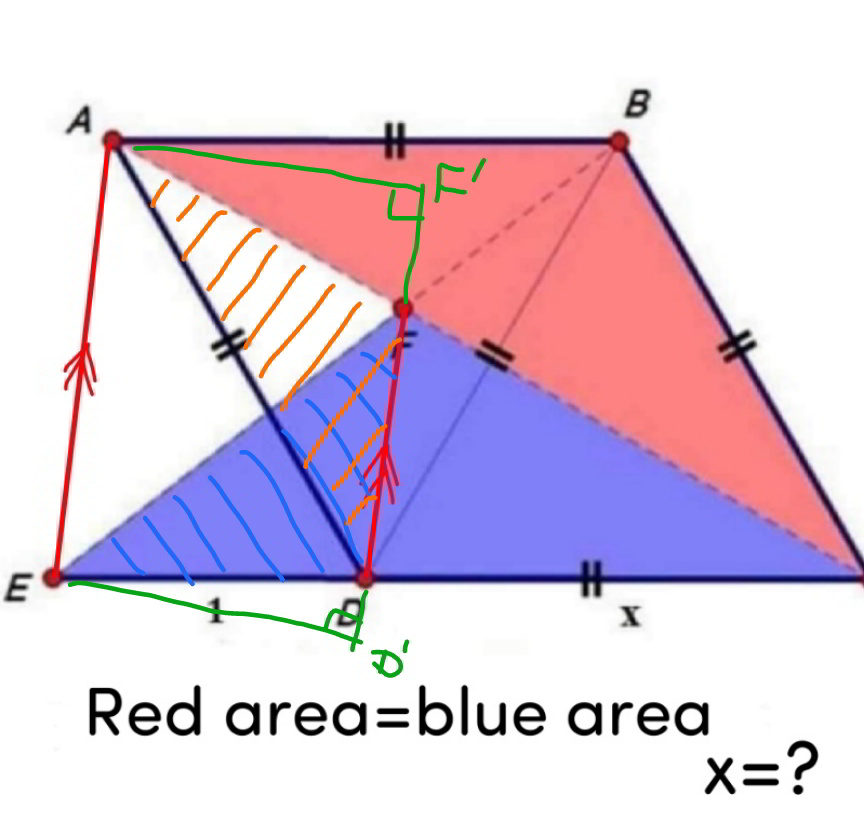
[ΔEFC]=[ΔADC] ⇒[ΔEFD]+[ΔDFC]=[ΔADF]+[ΔDFC] ⇒[ΔEFD]=[ΔADF] ⇒(1/2)DF×ED′=(1/2)×DF×AF′ ⇒ED′=AF′ ⇒EA//DF

$$\left[\Delta{EFC}\right]=\left[\Delta{ADC}\right] \\ $$$$\Rightarrow\left[\Delta{EFD}\right]+\left[\Delta{DFC}\right]=\left[\Delta{ADF}\right]+\left[\Delta{DFC}\right] \\ $$$$\Rightarrow\left[\Delta{EFD}\right]=\left[\Delta{ADF}\right] \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\mathrm{DF}×\mathrm{ED}'=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{DF}×\mathrm{AF}' \\ $$$$\Rightarrow\mathrm{ED}'=\mathrm{AF}' \\ $$$$\Rightarrow{EA}//{DF} \\ $$

Commented by amin96 last updated on 06/Jan/22

$$\boldsymbol{{VERY}}\:\boldsymbol{{NICE}}\: \\ $$

Commented by Tawa11 last updated on 06/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 06/Jan/22

Commented by mr W last updated on 06/Jan/22

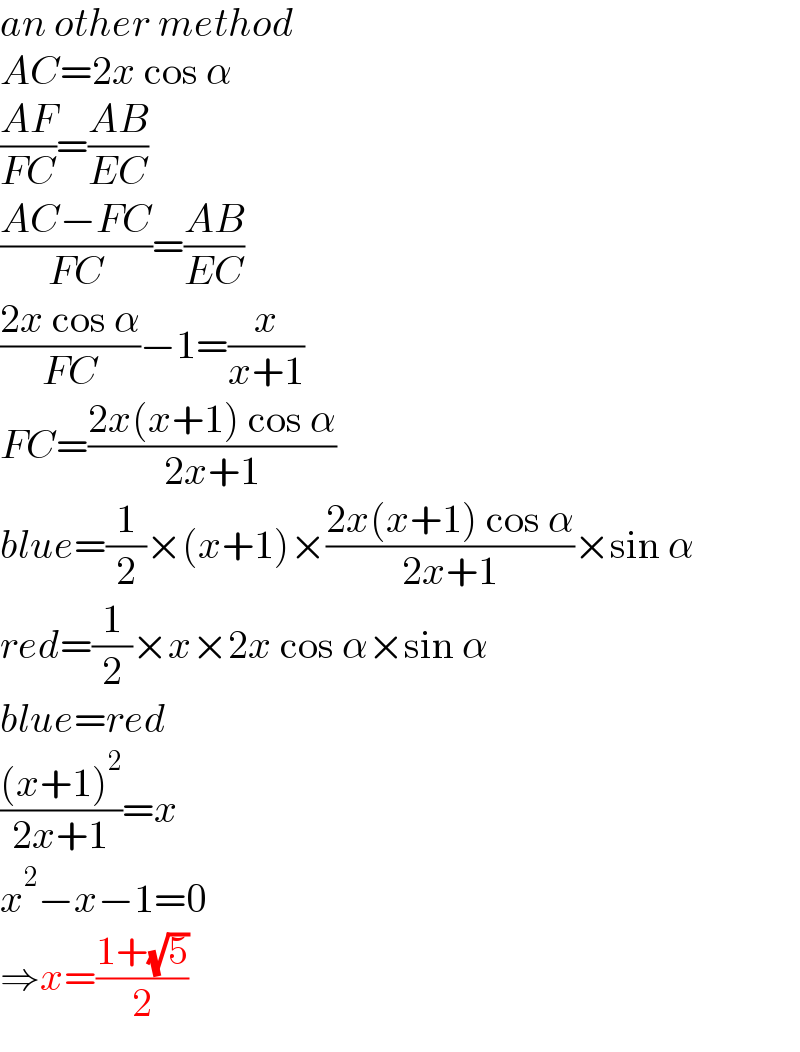
an other method AC=2x cos α ((AF)/(FC))=((AB)/(EC)) ((AC−FC)/(FC))=((AB)/(EC)) ((2x cos α)/(FC))−1=(x/(x+1)) FC=((2x(x+1) cos α)/(2x+1)) blue=(1/2)×(x+1)×((2x(x+1) cos α)/(2x+1))×sin α red=(1/2)×x×2x cos α×sin α blue=red (((x+1)^2 )/(2x+1))=x x^2 −x−1=0 ⇒x=((1+(√5))/2)

$${an}\:{other}\:{method} \\ $$$${AC}=\mathrm{2}{x}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{AF}}{{FC}}=\frac{{AB}}{{EC}} \\ $$$$\frac{{AC}−{FC}}{{FC}}=\frac{{AB}}{{EC}} \\ $$$$\frac{\mathrm{2}{x}\:\mathrm{cos}\:\alpha}{{FC}}−\mathrm{1}=\frac{{x}}{{x}+\mathrm{1}} \\ $$$${FC}=\frac{\mathrm{2}{x}\left({x}+\mathrm{1}\right)\:\mathrm{cos}\:\alpha}{\mathrm{2}{x}+\mathrm{1}} \\ $$$${blue}=\frac{\mathrm{1}}{\mathrm{2}}×\left({x}+\mathrm{1}\right)×\frac{\mathrm{2}{x}\left({x}+\mathrm{1}\right)\:\mathrm{cos}\:\alpha}{\mathrm{2}{x}+\mathrm{1}}×\mathrm{sin}\:\alpha \\ $$$${red}=\frac{\mathrm{1}}{\mathrm{2}}×{x}×\mathrm{2}{x}\:\mathrm{cos}\:\alpha×\mathrm{sin}\:\alpha \\ $$$${blue}={red} \\ $$$$\frac{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}{x}+\mathrm{1}}={x} \\ $$$${x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$

Commented by Tawa11 last updated on 07/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply