Question-163413

Question Number 163413 by mr W last updated on 06/Jan/22

Commented by mr W last updated on 06/Jan/22

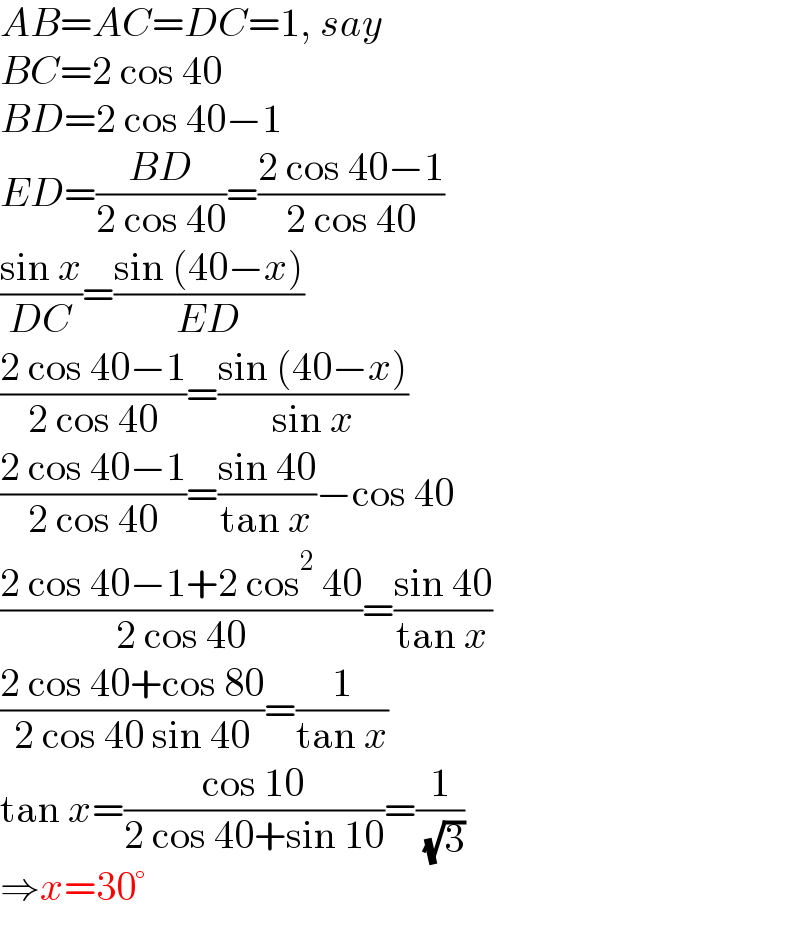
AB=AC=DC=1, say BC=2 cos 40 BD=2 cos 40−1 ED=((BD)/(2 cos 40))=((2 cos 40−1)/(2 cos 40)) ((sin x)/(DC))=((sin (40−x))/(ED)) ((2 cos 40−1)/(2 cos 40))=((sin (40−x))/(sin x)) ((2 cos 40−1)/(2 cos 40))=((sin 40)/(tan x))−cos 40 ((2 cos 40−1+2 cos^2 40)/(2 cos 40))=((sin 40)/(tan x)) ((2 cos 40+cos 80)/(2 cos 40 sin 40))=(1/(tan x)) tan x=((cos 10)/(2 cos 40+sin 10))=(1/( (√3))) ⇒x=30°

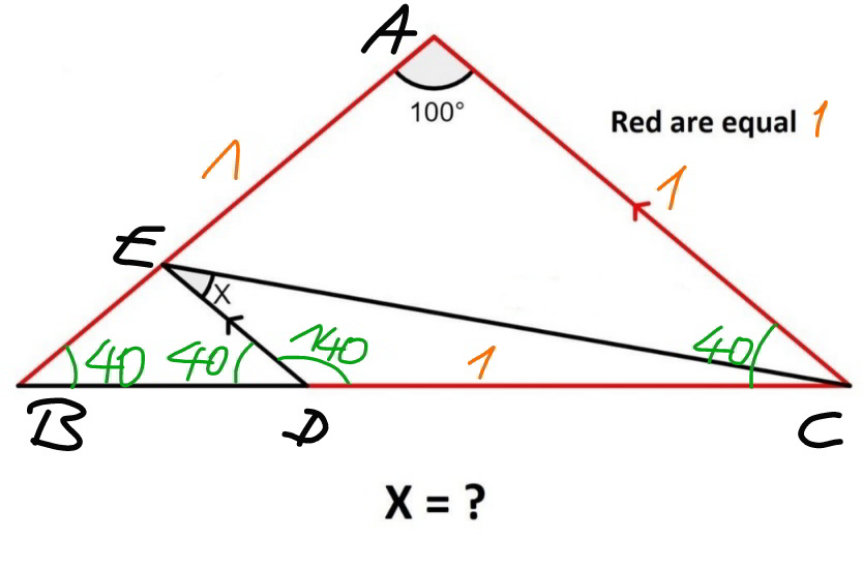
$${AB}={AC}={DC}=\mathrm{1},\:{say} \\ $$$${BC}=\mathrm{2}\:\mathrm{cos}\:\mathrm{40} \\ $$$${BD}=\mathrm{2}\:\mathrm{cos}\:\mathrm{40}−\mathrm{1} \\ $$$${ED}=\frac{{BD}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}−\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}} \\ $$$$\frac{\mathrm{sin}\:{x}}{{DC}}=\frac{\mathrm{sin}\:\left(\mathrm{40}−{x}\right)}{{ED}} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}−\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}}=\frac{\mathrm{sin}\:\left(\mathrm{40}−{x}\right)}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}−\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{tan}\:{x}}−\mathrm{cos}\:\mathrm{40} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}−\mathrm{1}+\mathrm{2}\:\mathrm{cos}^{\mathrm{2}} \:\mathrm{40}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}}=\frac{\mathrm{sin}\:\mathrm{40}}{\mathrm{tan}\:{x}} \\ $$$$\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}+\mathrm{cos}\:\mathrm{80}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}\:\mathrm{sin}\:\mathrm{40}}=\frac{\mathrm{1}}{\mathrm{tan}\:{x}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{cos}\:\mathrm{10}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{40}+\mathrm{sin}\:\mathrm{10}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow{x}=\mathrm{30}° \\ $$

Commented by amin96 last updated on 06/Jan/22

$${great}\:{sir} \\ $$

Commented by Tawa11 last updated on 06/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply