Question Number 163467 by Zaynal last updated on 07/Jan/22
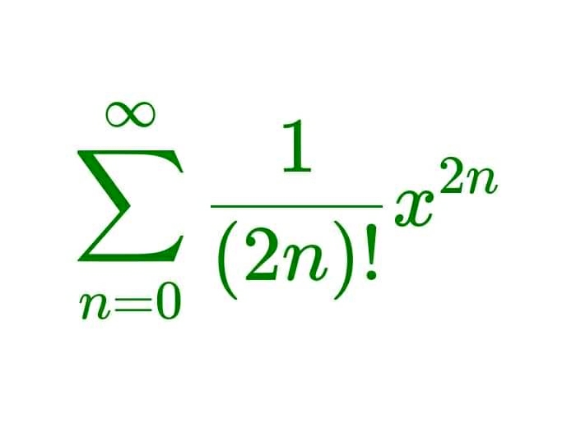
Answered by mr W last updated on 07/Jan/22
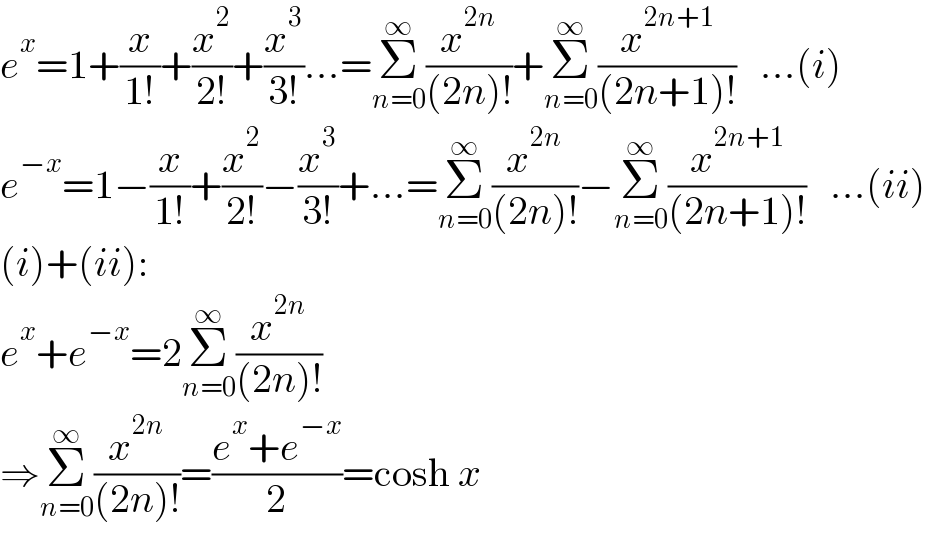
$${e}^{{x}} =\mathrm{1}+\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}…=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:\:…\left({i}\right) \\ $$$${e}^{−{x}} =\mathrm{1}−\frac{{x}}{\mathrm{1}!}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$${e}^{{x}} +{e}^{−{x}} =\mathrm{2}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$$\Rightarrow\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!}=\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}=\mathrm{cosh}\:{x} \\ $$
Commented by Tawa11 last updated on 07/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
