Question-163483

Question Number 163483 by Zaynal last updated on 07/Jan/22

Answered by alephzero last updated on 07/Jan/22

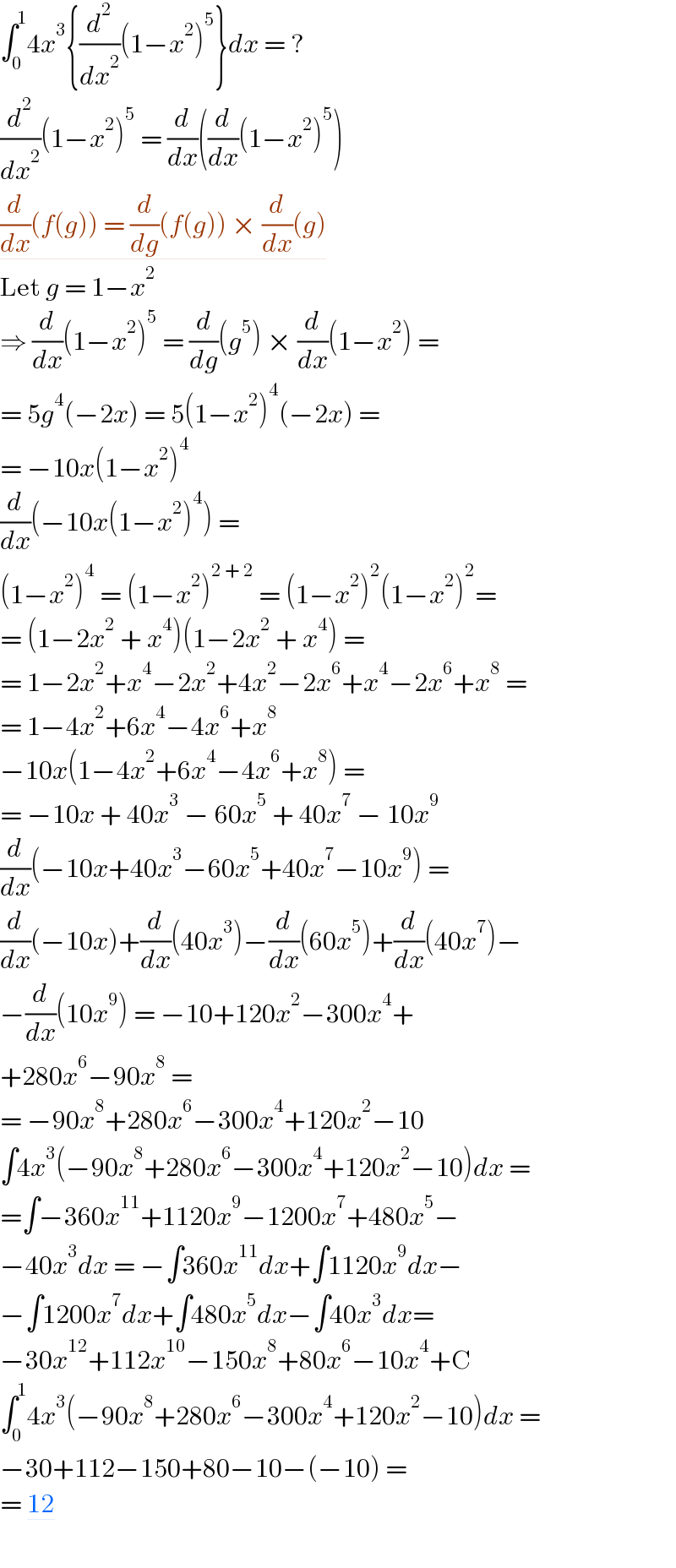
∫_0 ^1 4x^3 {(d^2 /dx^2 )(1−x^2 )^5 }dx = ? (d^2 /dx^2 )(1−x^2 )^5 = (d/dx)((d/dx)(1−x^2 )^5 ) (d/dx)(f(g)) = (d/dg)(f(g)) × (d/dx)(g) Let g = 1−x^2 ⇒ (d/dx)(1−x^2 )^5 = (d/dg)(g^5 ) × (d/dx)(1−x^2 ) = = 5g^4 (−2x) = 5(1−x^2 )^4 (−2x) = = −10x(1−x^2 )^4 (d/dx)(−10x(1−x^2 )^4 ) = (1−x^2 )^4 = (1−x^2 )^(2 + 2) = (1−x^2 )^2 (1−x^2 )^2 = = (1−2x^2 + x^4 )(1−2x^2 + x^4 ) = = 1−2x^2 +x^4 −2x^2 +4x^2 −2x^6 +x^4 −2x^6 +x^8 = = 1−4x^2 +6x^4 −4x^6 +x^8 −10x(1−4x^2 +6x^4 −4x^6 +x^8 ) = = −10x + 40x^3 − 60x^5 + 40x^7 − 10x^9 (d/dx)(−10x+40x^3 −60x^5 +40x^7 −10x^9 ) = (d/dx)(−10x)+(d/dx)(40x^3 )−(d/dx)(60x^5 )+(d/dx)(40x^7 )− −(d/dx)(10x^9 ) = −10+120x^2 −300x^4 + +280x^6 −90x^8 = = −90x^8 +280x^6 −300x^4 +120x^2 −10 ∫4x^3 (−90x^8 +280x^6 −300x^4 +120x^2 −10)dx = =∫−360x^(11) +1120x^9 −1200x^7 +480x^5 − −40x^3 dx = −∫360x^(11) dx+∫1120x^9 dx− −∫1200x^7 dx+∫480x^5 dx−∫40x^3 dx= −30x^(12) +112x^(10) −150x^8 +80x^6 −10x^4 +C ∫_0 ^1 4x^3 (−90x^8 +280x^6 −300x^4 +120x^2 −10)dx = −30+112−150+80−10−(−10) = = 12

$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left\{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right\}{dx}\:=\:? \\ $$$$\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \:=\:\frac{{d}}{{dx}}\left(\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right) \\ $$$$\underline{\frac{{d}}{{dx}}\left({f}\left({g}\right)\right)\:=\:\frac{{d}}{{dg}}\left({f}\left({g}\right)\right)\:×\:\frac{{d}}{{dx}}\left({g}\right)} \\ $$$$\mathrm{Let}\:{g}\:=\:\mathrm{1}−{x}^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \:=\:\frac{{d}}{{dg}}\left({g}^{\mathrm{5}} \right)\:×\:\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:= \\ $$$$=\:\mathrm{5}{g}^{\mathrm{4}} \left(−\mathrm{2}{x}\right)\:=\:\mathrm{5}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \left(−\mathrm{2}{x}\right)\:= \\ $$$$=\:−\mathrm{10}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \\ $$$$\frac{{d}}{{dx}}\left(−\mathrm{10}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \right)\:=\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \:=\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}\:+\:\mathrm{2}} \:=\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} = \\ $$$$=\:\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \right)\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:+\:{x}^{\mathrm{4}} \right)\:= \\ $$$$=\:\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} −\mathrm{2}{x}^{\mathrm{6}} +{x}^{\mathrm{4}} −\mathrm{2}{x}^{\mathrm{6}} +{x}^{\mathrm{8}} \:= \\ $$$$=\:\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{6}} +{x}^{\mathrm{8}} \\ $$$$−\mathrm{10}{x}\left(\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{6}} +{x}^{\mathrm{8}} \right)\:=\: \\ $$$$=\:−\mathrm{10}{x}\:+\:\mathrm{40}{x}^{\mathrm{3}} \:−\:\mathrm{60}{x}^{\mathrm{5}} \:+\:\mathrm{40}{x}^{\mathrm{7}} \:−\:\mathrm{10}{x}^{\mathrm{9}} \\ $$$$\frac{{d}}{{dx}}\left(−\mathrm{10}{x}+\mathrm{40}{x}^{\mathrm{3}} −\mathrm{60}{x}^{\mathrm{5}} +\mathrm{40}{x}^{\mathrm{7}} −\mathrm{10}{x}^{\mathrm{9}} \right)\:= \\ $$$$\frac{{d}}{{dx}}\left(−\mathrm{10}{x}\right)+\frac{{d}}{{dx}}\left(\mathrm{40}{x}^{\mathrm{3}} \right)−\frac{{d}}{{dx}}\left(\mathrm{60}{x}^{\mathrm{5}} \right)+\frac{{d}}{{dx}}\left(\mathrm{40}{x}^{\mathrm{7}} \right)− \\ $$$$−\frac{{d}}{{dx}}\left(\mathrm{10}{x}^{\mathrm{9}} \right)\:=\:−\mathrm{10}+\mathrm{120}{x}^{\mathrm{2}} −\mathrm{300}{x}^{\mathrm{4}} + \\ $$$$+\mathrm{280}{x}^{\mathrm{6}} −\mathrm{90}{x}^{\mathrm{8}} \:= \\ $$$$=\:−\mathrm{90}{x}^{\mathrm{8}} +\mathrm{280}{x}^{\mathrm{6}} −\mathrm{300}{x}^{\mathrm{4}} +\mathrm{120}{x}^{\mathrm{2}} −\mathrm{10} \\ $$$$\int\mathrm{4}{x}^{\mathrm{3}} \left(−\mathrm{90}{x}^{\mathrm{8}} +\mathrm{280}{x}^{\mathrm{6}} −\mathrm{300}{x}^{\mathrm{4}} +\mathrm{120}{x}^{\mathrm{2}} −\mathrm{10}\right){dx}\:= \\ $$$$=\int−\mathrm{360}{x}^{\mathrm{11}} +\mathrm{1120}{x}^{\mathrm{9}} −\mathrm{1200}{x}^{\mathrm{7}} +\mathrm{480}{x}^{\mathrm{5}} − \\ $$$$−\mathrm{40}{x}^{\mathrm{3}} {dx}\:=\:−\int\mathrm{360}{x}^{\mathrm{11}} {dx}+\int\mathrm{1120}{x}^{\mathrm{9}} {dx}− \\ $$$$−\int\mathrm{1200}{x}^{\mathrm{7}} {dx}+\int\mathrm{480}{x}^{\mathrm{5}} {dx}−\int\mathrm{40}{x}^{\mathrm{3}} {dx}= \\ $$$$−\mathrm{30}{x}^{\mathrm{12}} +\mathrm{112}{x}^{\mathrm{10}} −\mathrm{150}{x}^{\mathrm{8}} +\mathrm{80}{x}^{\mathrm{6}} −\mathrm{10}{x}^{\mathrm{4}} +\mathrm{C} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left(−\mathrm{90}{x}^{\mathrm{8}} +\mathrm{280}{x}^{\mathrm{6}} −\mathrm{300}{x}^{\mathrm{4}} +\mathrm{120}{x}^{\mathrm{2}} −\mathrm{10}\right){dx}\:= \\ $$$$−\mathrm{30}+\mathrm{112}−\mathrm{150}+\mathrm{80}−\mathrm{10}−\left(−\mathrm{10}\right)\:= \\ $$$$=\:\underline{\mathrm{12}} \\ $$

Commented by Zaynal last updated on 07/Jan/22

$$\mathrm{ans}\:\mathrm{is}\:\mathrm{2} \\ $$

Answered by mr W last updated on 07/Jan/22

(d/dx)(1−x^2 )^5 =5(1−x^2 )^4 (−2x) (d^2 /dx^2 )(1−x^2 )^5 =−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 ∫_0 ^1 4x^3 {−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 }dx =∫_0 ^1 2x^2 {−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 }d(x^2 ) =20∫_0 ^1 u(9u−1)(1−u)^3 du =20∫_0 ^1 (u−1+1)(−9(u−1)−8)(u−1)^3 d(u−1) =20∫_(−1) ^0 (t+1)(−9t−8)t^3 dt =20∫_0 ^(−1) (t+1)(9t+8)t^3 dt =20∫_0 ^(−1) (9t^5 +17t^4 +8t^3 )dt =20[((3t^6 )/2)+((17t^5 )/5)+2t^4 ]_0 ^(−1) dt =20((3/2)−((17)/5)+2) =20×(1/(10)) =2

$$\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} =\mathrm{5}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \left(−\mathrm{2}{x}\right) \\ $$$$\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} =−\mathrm{10}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} +\mathrm{80}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left\{−\mathrm{10}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} +\mathrm{80}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} \right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{x}^{\mathrm{2}} \left\{−\mathrm{10}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} +\mathrm{80}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} \right\}{d}\left({x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{20}\int_{\mathrm{0}} ^{\mathrm{1}} {u}\left(\mathrm{9}{u}−\mathrm{1}\right)\left(\mathrm{1}−{u}\right)^{\mathrm{3}} {du} \\ $$$$=\mathrm{20}\int_{\mathrm{0}} ^{\mathrm{1}} \left({u}−\mathrm{1}+\mathrm{1}\right)\left(−\mathrm{9}\left({u}−\mathrm{1}\right)−\mathrm{8}\right)\left({u}−\mathrm{1}\right)^{\mathrm{3}} {d}\left({u}−\mathrm{1}\right) \\ $$$$=\mathrm{20}\int_{−\mathrm{1}} ^{\mathrm{0}} \left({t}+\mathrm{1}\right)\left(−\mathrm{9}{t}−\mathrm{8}\right){t}^{\mathrm{3}} {dt} \\ $$$$=\mathrm{20}\int_{\mathrm{0}} ^{−\mathrm{1}} \left({t}+\mathrm{1}\right)\left(\mathrm{9}{t}+\mathrm{8}\right){t}^{\mathrm{3}} {dt} \\ $$$$=\mathrm{20}\int_{\mathrm{0}} ^{−\mathrm{1}} \left(\mathrm{9}{t}^{\mathrm{5}} +\mathrm{17}{t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{3}} \right){dt} \\ $$$$=\mathrm{20}\left[\frac{\mathrm{3}{t}^{\mathrm{6}} }{\mathrm{2}}+\frac{\mathrm{17}{t}^{\mathrm{5}} }{\mathrm{5}}+\mathrm{2}{t}^{\mathrm{4}} \right]_{\mathrm{0}} ^{−\mathrm{1}} {dt} \\ $$$$=\mathrm{20}\left(\frac{\mathrm{3}}{\mathrm{2}}−\frac{\mathrm{17}}{\mathrm{5}}+\mathrm{2}\right) \\ $$$$=\mathrm{20}×\frac{\mathrm{1}}{\mathrm{10}} \\ $$$$=\mathrm{2} \\ $$

Answered by Ar Brandon last updated on 07/Jan/22

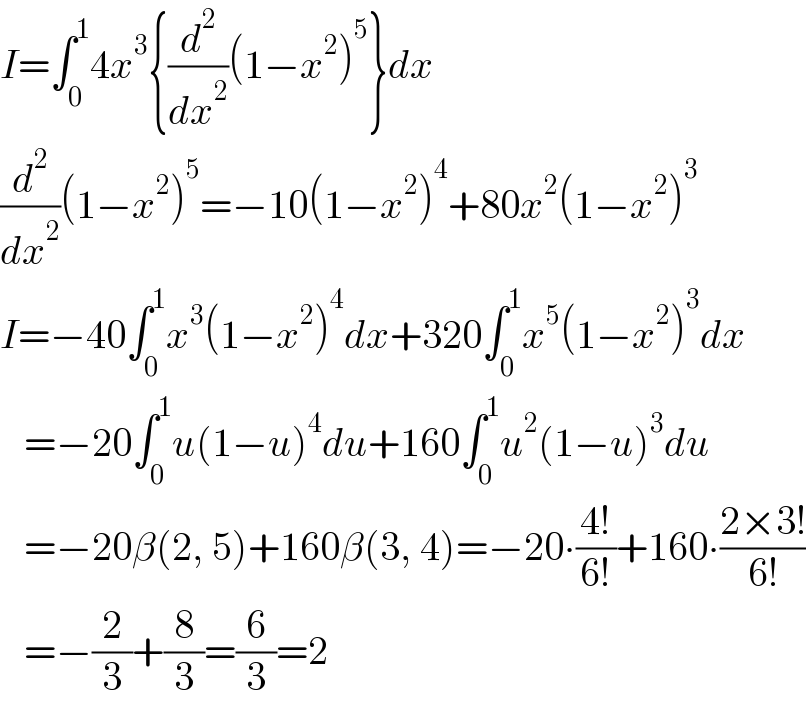
I=∫_0 ^1 4x^3 {(d^2 /dx^2 )(1−x^2 )^5 }dx (d^2 /dx^2 )(1−x^2 )^5 =−10(1−x^2 )^4 +80x^2 (1−x^2 )^3 I=−40∫_0 ^1 x^3 (1−x^2 )^4 dx+320∫_0 ^1 x^5 (1−x^2 )^3 dx =−20∫_0 ^1 u(1−u)^4 du+160∫_0 ^1 u^2 (1−u)^3 du =−20β(2, 5)+160β(3, 4)=−20∙((4!)/(6!))+160∙((2×3!)/(6!)) =−(2/3)+(8/3)=(6/3)=2

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left\{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right\}{dx} \\ $$$$\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} =−\mathrm{10}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} +\mathrm{80}{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} \\ $$$${I}=−\mathrm{40}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{3}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} {dx}+\mathrm{320}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{5}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} {dx} \\ $$$$\:\:\:=−\mathrm{20}\int_{\mathrm{0}} ^{\mathrm{1}} {u}\left(\mathrm{1}−{u}\right)^{\mathrm{4}} {du}+\mathrm{160}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{2}} \left(\mathrm{1}−{u}\right)^{\mathrm{3}} {du} \\ $$$$\:\:\:=−\mathrm{20}\beta\left(\mathrm{2},\:\mathrm{5}\right)+\mathrm{160}\beta\left(\mathrm{3},\:\mathrm{4}\right)=−\mathrm{20}\centerdot\frac{\mathrm{4}!}{\mathrm{6}!}+\mathrm{160}\centerdot\frac{\mathrm{2}×\mathrm{3}!}{\mathrm{6}!} \\ $$$$\:\:\:=−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{8}}{\mathrm{3}}=\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2} \\ $$

Answered by ajfour last updated on 07/Jan/22

x^2 =t ∫_0 ^( 1) 2t{(d^2 /dx^2 )(1−x^2 )^5 }dt =∫(d/dx){5(−2x)(1−x^2 )^4 }2tdt =5∫_0 ^( 1) {16t(1−t)^3 −2(1−t)^4 }(2tdt) =10∫_0 ^( 1) {16(1−t)t^3 −2t^4 }(1−t)dt =10∫{16t^3 −18t^4 )(1−t)dt =10∫_0 ^( 1) (16t^3 −16t^4 −18t^4 +18t^5 )dt =10[4−((34)/5)+3]=70−68 = 2 (got it).

$${x}^{\mathrm{2}} ={t} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{2}{t}\left\{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right\}{dt} \\ $$$$=\int\frac{{d}}{{dx}}\left\{\mathrm{5}\left(−\mathrm{2}{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{4}} \right\}\mathrm{2}{tdt} \\ $$$$=\mathrm{5}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\mathrm{16}{t}\left(\mathrm{1}−{t}\right)^{\mathrm{3}} −\mathrm{2}\left(\mathrm{1}−{t}\right)^{\mathrm{4}} \right\}\left(\mathrm{2}{tdt}\right) \\ $$$$=\mathrm{10}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left\{\mathrm{16}\left(\mathrm{1}−{t}\right){t}^{\mathrm{3}} −\mathrm{2}{t}^{\mathrm{4}} \right\}\left(\mathrm{1}−{t}\right){dt} \\ $$$$=\mathrm{10}\int\left\{\mathrm{16}{t}^{\mathrm{3}} −\mathrm{18}{t}^{\mathrm{4}} \right)\left(\mathrm{1}−{t}\right){dt} \\ $$$$=\mathrm{10}\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\mathrm{16}{t}^{\mathrm{3}} −\mathrm{16}{t}^{\mathrm{4}} −\mathrm{18}{t}^{\mathrm{4}} +\mathrm{18}{t}^{\mathrm{5}} \right){dt} \\ $$$$=\mathrm{10}\left[\mathrm{4}−\frac{\mathrm{34}}{\mathrm{5}}+\mathrm{3}\right]=\mathrm{70}−\mathrm{68}\:=\:\mathrm{2}\:\:\left({got}\:{it}\right). \\ $$$$ \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply