Question-163522

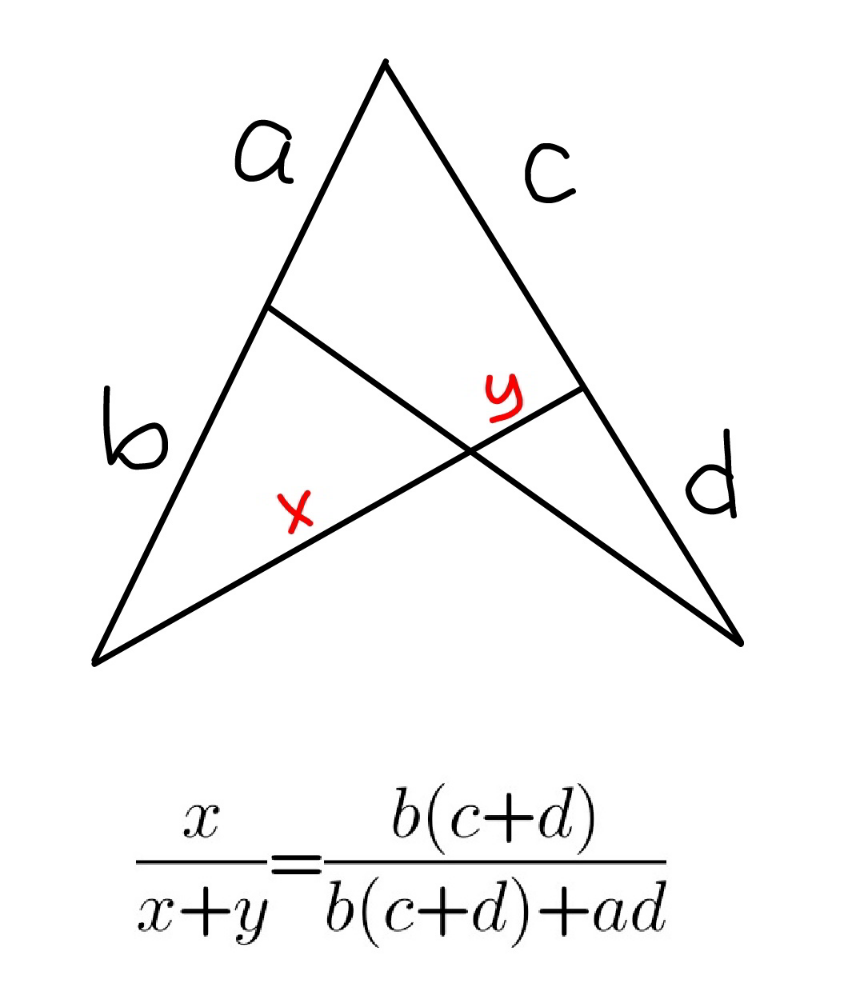
Question Number 163522 by nurtani last updated on 07/Jan/22

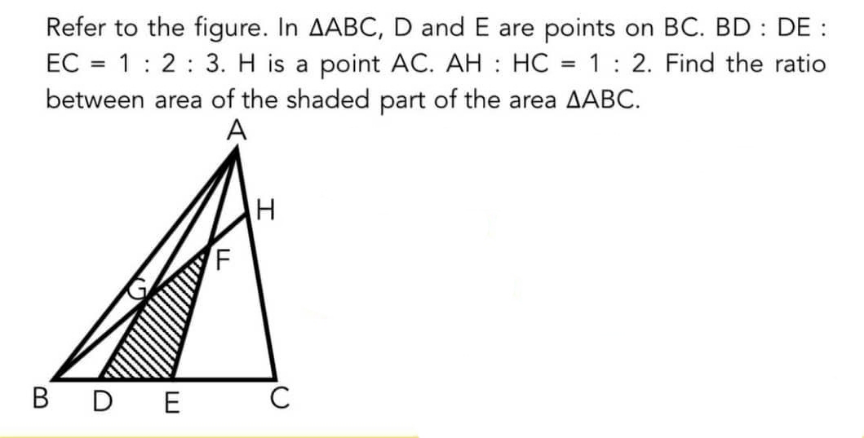
Answered by ajfour last updated on 08/Jan/22

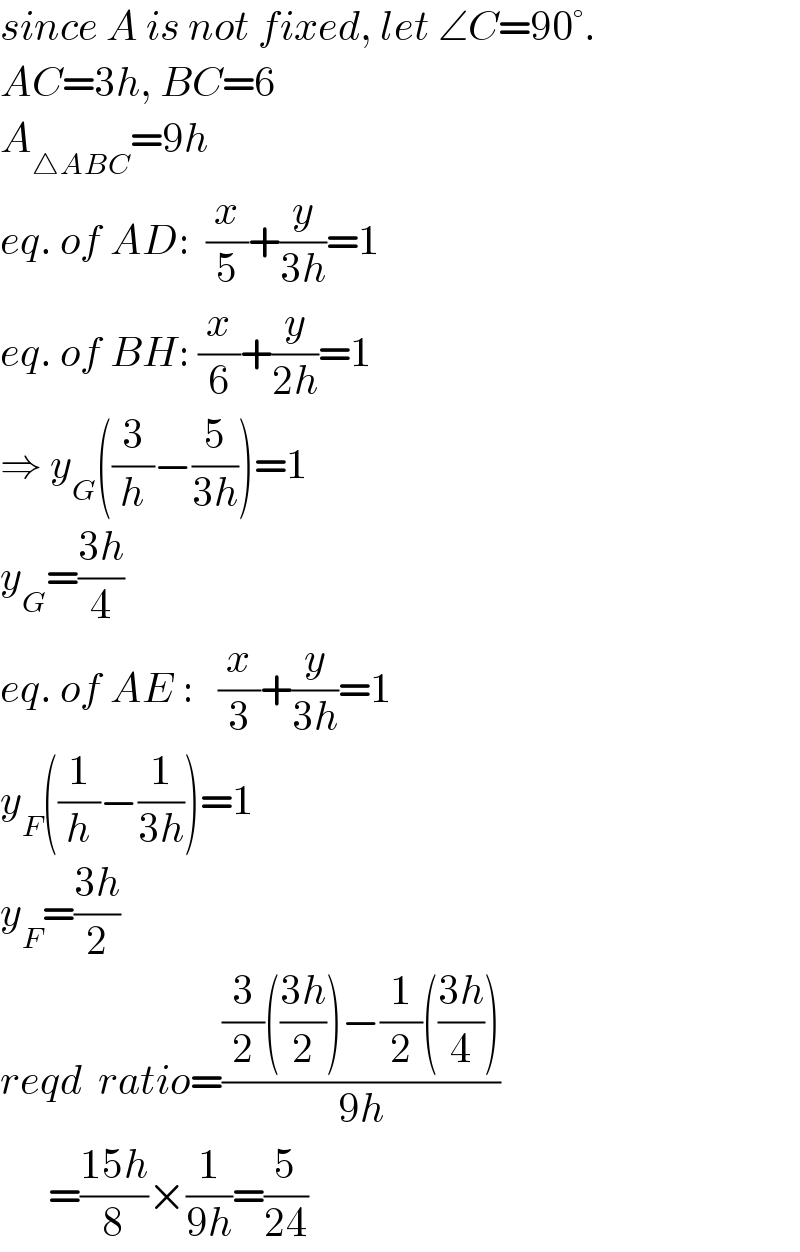
since A is not fixed, let ∠C=90°. AC=3h, BC=6 A_(△ABC) =9h eq. of AD: (x/5)+(y/(3h))=1 eq. of BH: (x/6)+(y/(2h))=1 ⇒ y_G ((3/h)−(5/(3h)))=1 y_G =((3h)/4) eq. of AE : (x/3)+(y/(3h))=1 y_F ((1/h)−(1/(3h)))=1 y_F =((3h)/2) reqd ratio=(((3/2)(((3h)/2))−(1/2)(((3h)/4)))/(9h)) =((15h)/8)×(1/(9h))=(5/(24))

$${since}\:{A}\:{is}\:{not}\:{fixed},\:{let}\:\angle{C}=\mathrm{90}°. \\ $$$${AC}=\mathrm{3}{h},\:{BC}=\mathrm{6} \\ $$$${A}_{\bigtriangleup{ABC}} =\mathrm{9}{h} \\ $$$${eq}.\:{of}\:{AD}:\:\:\frac{{x}}{\mathrm{5}}+\frac{{y}}{\mathrm{3}{h}}=\mathrm{1} \\ $$$${eq}.\:{of}\:{BH}:\:\frac{{x}}{\mathrm{6}}+\frac{{y}}{\mathrm{2}{h}}=\mathrm{1} \\ $$$$\Rightarrow\:{y}_{{G}} \left(\frac{\mathrm{3}}{{h}}−\frac{\mathrm{5}}{\mathrm{3}{h}}\right)=\mathrm{1} \\ $$$${y}_{{G}} =\frac{\mathrm{3}{h}}{\mathrm{4}} \\ $$$${eq}.\:{of}\:{AE}\::\:\:\:\frac{{x}}{\mathrm{3}}+\frac{{y}}{\mathrm{3}{h}}=\mathrm{1} \\ $$$${y}_{{F}} \left(\frac{\mathrm{1}}{{h}}−\frac{\mathrm{1}}{\mathrm{3}{h}}\right)=\mathrm{1} \\ $$$${y}_{{F}} =\frac{\mathrm{3}{h}}{\mathrm{2}} \\ $$$${reqd}\:\:{ratio}=\frac{\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{3}{h}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{3}{h}}{\mathrm{4}}\right)}{\mathrm{9}{h}} \\ $$$$\:\:\:\:\:\:=\frac{\mathrm{15}{h}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{9}{h}}=\frac{\mathrm{5}}{\mathrm{24}} \\ $$

Commented by Tawa11 last updated on 09/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Answered by mr W last updated on 07/Jan/22

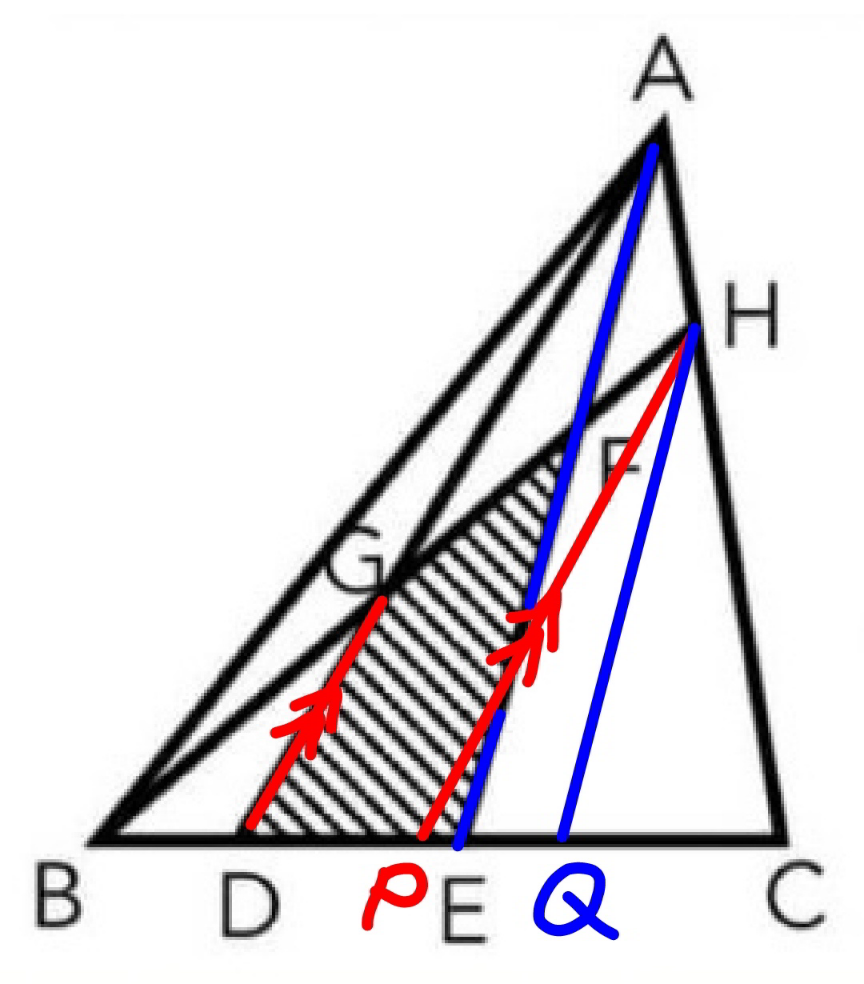
Commented by Tawa11 last updated on 09/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Commented by mr W last updated on 07/Jan/22

((DP)/(DC))=((AH)/(AC))=(1/3) DP=((DC)/3)=(1/3)×((5BC)/6)=((5BC)/(18))=((5×6BD)/(18))=((5BD)/3) ((BG)/(GH))=((BD)/(DP))=(3/5) ⇒((BG)/(BH))=(3/8) ((EQ)/(EC))=((AH)/(AC))=(1/3) EQ=((EC)/3)=((BE)/3) ((FH)/(BF))=((EQ)/(BE))=(1/3) ⇒((FH)/(BH))=(1/4)=(2/8) ((GF)/(BH))=((8−3−2)/8)=(3/8) [AGF]=(3/8)[ABH]=(3/8)×(1/3)[ABC]=(([ABC])/8) [ADB]=(2/6)[ABC]=(([ABC])/3) [DGFE]=[ADB]−[AGF]=(([ABC])/3)−(([ABC])/8)=(5/(24))[ABC] ⇒(([DGFE])/([ABC]))=(5/(24))

$$\frac{{DP}}{{DC}}=\frac{{AH}}{{AC}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${DP}=\frac{{DC}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{5}{BC}}{\mathrm{6}}=\frac{\mathrm{5}{BC}}{\mathrm{18}}=\frac{\mathrm{5}×\mathrm{6}{BD}}{\mathrm{18}}=\frac{\mathrm{5}{BD}}{\mathrm{3}} \\ $$$$\frac{{BG}}{{GH}}=\frac{{BD}}{{DP}}=\frac{\mathrm{3}}{\mathrm{5}}\:\Rightarrow\frac{{BG}}{{BH}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\frac{{EQ}}{{EC}}=\frac{{AH}}{{AC}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${EQ}=\frac{{EC}}{\mathrm{3}}=\frac{{BE}}{\mathrm{3}} \\ $$$$\frac{{FH}}{{BF}}=\frac{{EQ}}{{BE}}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\frac{{FH}}{{BH}}=\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{2}}{\mathrm{8}} \\ $$$$\frac{{GF}}{{BH}}=\frac{\mathrm{8}−\mathrm{3}−\mathrm{2}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\left[{AGF}\right]=\frac{\mathrm{3}}{\mathrm{8}}\left[{ABH}\right]=\frac{\mathrm{3}}{\mathrm{8}}×\frac{\mathrm{1}}{\mathrm{3}}\left[{ABC}\right]=\frac{\left[{ABC}\right]}{\mathrm{8}} \\ $$$$\left[{ADB}\right]=\frac{\mathrm{2}}{\mathrm{6}}\left[{ABC}\right]=\frac{\left[{ABC}\right]}{\mathrm{3}} \\ $$$$\left[{DGFE}\right]=\left[{ADB}\right]−\left[{AGF}\right]=\frac{\left[{ABC}\right]}{\mathrm{3}}−\frac{\left[{ABC}\right]}{\mathrm{8}}=\frac{\mathrm{5}}{\mathrm{24}}\left[{ABC}\right] \\ $$$$\Rightarrow\frac{\left[{DGFE}\right]}{\left[{ABC}\right]}=\frac{\mathrm{5}}{\mathrm{24}} \\ $$

Commented by nurtani last updated on 08/Jan/22

nice Mr W, thank you��

Answered by mr W last updated on 08/Jan/22

alternative method ((AG)/(AD))=((1×6)/(1×6+2×1))=(3/4) ((AF)/(AE))=((1×6)/(1×6+2×3))=(1/2) [AGF]=(3/4)×(1/2)×[ADE]=(3/8)[ADE] [DGFE]=(5/8)[ADE]=(5/8)×(([ABC])/3)=((5[ABC])/(24)) (([DGFE])/([ABC]))=(5/(24))

$$\underline{\boldsymbol{{alternative}}\:\boldsymbol{{method}}} \\ $$$$\frac{{AG}}{{AD}}=\frac{\mathrm{1}×\mathrm{6}}{\mathrm{1}×\mathrm{6}+\mathrm{2}×\mathrm{1}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{{AF}}{{AE}}=\frac{\mathrm{1}×\mathrm{6}}{\mathrm{1}×\mathrm{6}+\mathrm{2}×\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left[{AGF}\right]=\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{1}}{\mathrm{2}}×\left[{ADE}\right]=\frac{\mathrm{3}}{\mathrm{8}}\left[{ADE}\right] \\ $$$$\left[{DGFE}\right]=\frac{\mathrm{5}}{\mathrm{8}}\left[{ADE}\right]=\frac{\mathrm{5}}{\mathrm{8}}×\frac{\left[{ABC}\right]}{\mathrm{3}}=\frac{\mathrm{5}\left[{ABC}\right]}{\mathrm{24}} \\ $$$$\frac{\left[{DGFE}\right]}{\left[{ABC}\right]}=\frac{\mathrm{5}}{\mathrm{24}} \\ $$

Commented by mr W last updated on 09/Jan/22

Facebook Tweet Pin

Leave a Reply Cancel reply