Question Number 16354 by Tinkutara last updated on 21/Jun/17
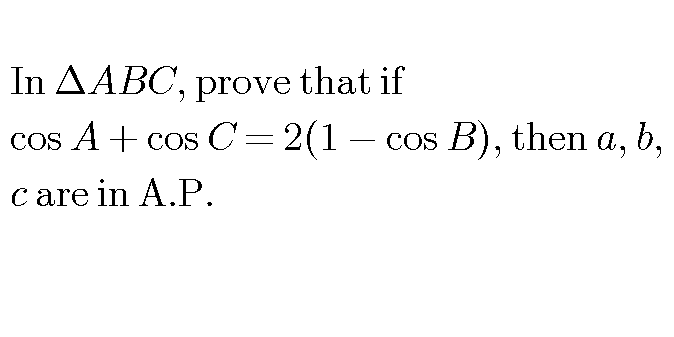
Answered by myintkhaing last updated on 21/Jun/17
![((b^2 +c^2 −a^2 )/(2bc))+((a^2 +b^2 −c^2 )/(2ab))=2−((c^2 +a^2 −b^2 )/(ca)) (1/(2b))(((ab^2 +ac^2 −a^3 +a^2 c+b^2 c−c^3 )/(ca)))=((2ca−c^2 −a^2 +b^2 )/(ca)) (1/(2b))[b^2 (a+c)+ac(a+c)−(a+c)(a^2 −ac+c^2 ))=b^2 −(a−c)^2 (1/(2b))[(a+c)(b^2 +ac−a^2 +ac−c^2 )]=b^2 −(a−c)^2 (1/(2b))[(a+c)(b^2 −(a−c)^2 ]=b^2 −(a−c)^2 a+c = 2b ∴ a, b and c are in A.P..](https://www.tinkutara.com/question/Q16356.png)
$$\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}}+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}=\mathrm{2}−\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{{ca}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}}\left(\frac{{ab}^{\mathrm{2}} +{ac}^{\mathrm{2}} −{a}^{\mathrm{3}} +{a}^{\mathrm{2}} {c}+{b}^{\mathrm{2}} {c}−{c}^{\mathrm{3}} }{{ca}}\right)=\frac{\mathrm{2}{ca}−{c}^{\mathrm{2}} −{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{{ca}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}}\left[{b}^{\mathrm{2}} \left({a}+{c}\right)+{ac}\left({a}+{c}\right)−\left({a}+{c}\right)\left({a}^{\mathrm{2}} −{ac}+{c}^{\mathrm{2}} \right)\right)={b}^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}}\left[\left({a}+{c}\right)\left({b}^{\mathrm{2}} +{ac}−{a}^{\mathrm{2}} +{ac}−{c}^{\mathrm{2}} \right)\right]={b}^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{b}}\left[\left({a}+{c}\right)\left({b}^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} \right]={b}^{\mathrm{2}} −\left({a}−{c}\right)^{\mathrm{2}} \right. \\ $$$${a}+{c}\:=\:\mathrm{2}{b} \\ $$$$\therefore\:{a},\:{b}\:{and}\:{c}\:{are}\:{in}\:{A}.{P}.. \\ $$
Commented by Tinkutara last updated on 21/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
