Question Number 163556 by Ari last updated on 07/Jan/22
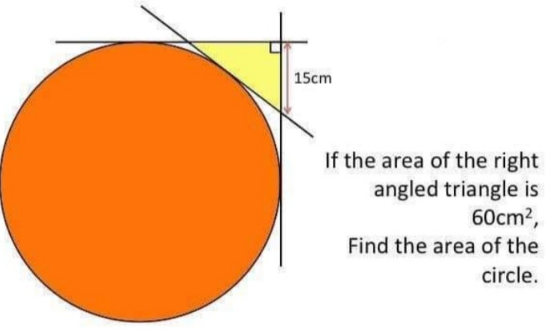
Answered by ajfour last updated on 07/Jan/22
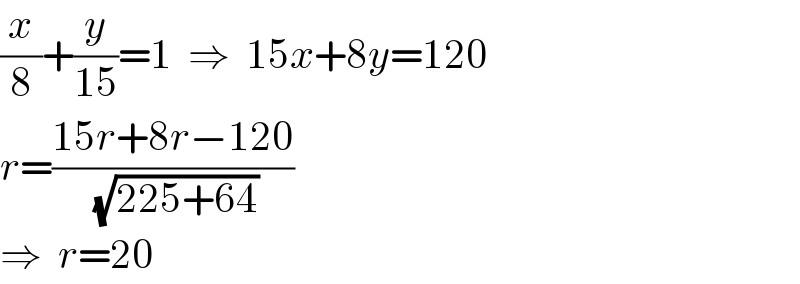
$$\frac{{x}}{\mathrm{8}}+\frac{{y}}{\mathrm{15}}=\mathrm{1}\:\:\Rightarrow\:\:\mathrm{15}{x}+\mathrm{8}{y}=\mathrm{120} \\ $$$${r}=\frac{\mathrm{15}{r}+\mathrm{8}{r}−\mathrm{120}}{\:\sqrt{\mathrm{225}+\mathrm{64}}} \\ $$$$\Rightarrow\:\:{r}=\mathrm{20} \\ $$
Answered by mr W last updated on 07/Jan/22
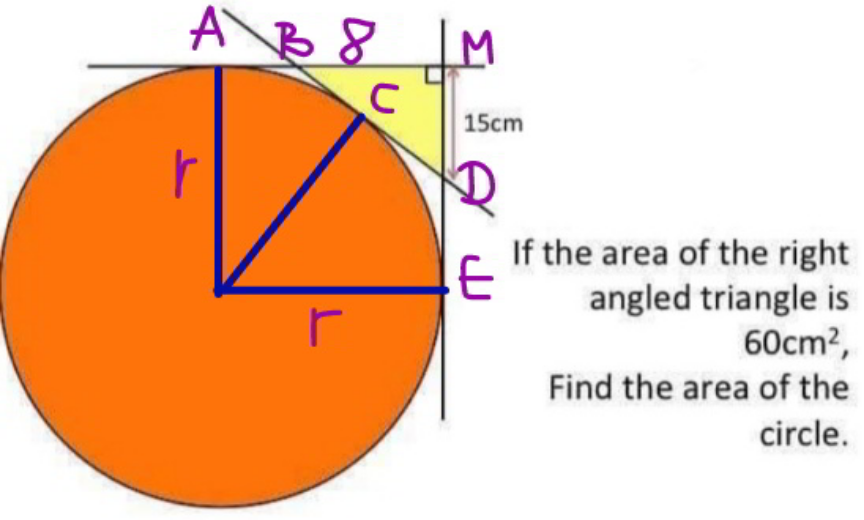
Commented by mr W last updated on 07/Jan/22
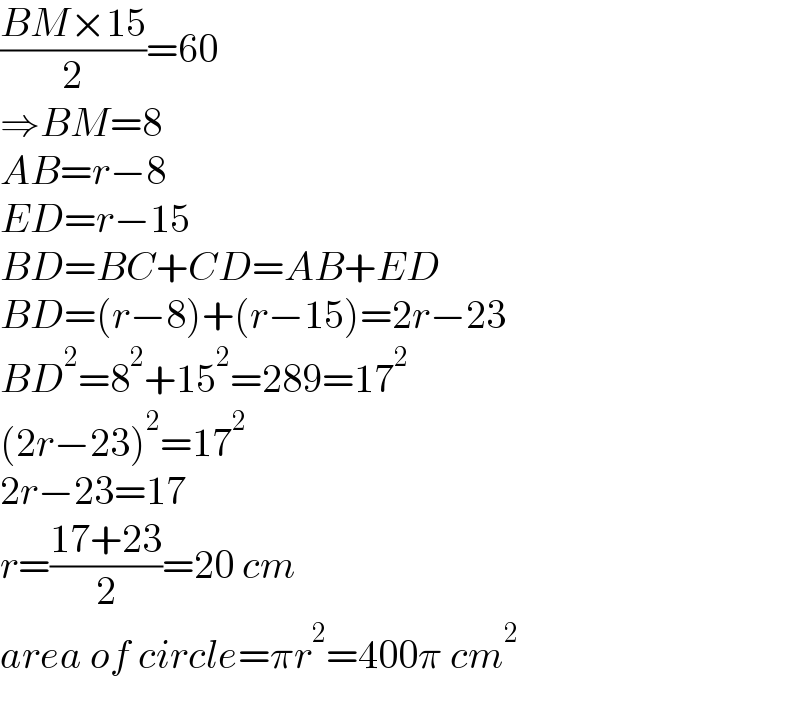
$$\frac{{BM}×\mathrm{15}}{\mathrm{2}}=\mathrm{60} \\ $$$$\Rightarrow{BM}=\mathrm{8} \\ $$$${AB}={r}−\mathrm{8} \\ $$$${ED}={r}−\mathrm{15} \\ $$$${BD}={BC}+{CD}={AB}+{ED} \\ $$$${BD}=\left({r}−\mathrm{8}\right)+\left({r}−\mathrm{15}\right)=\mathrm{2}{r}−\mathrm{23} \\ $$$${BD}^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} +\mathrm{15}^{\mathrm{2}} =\mathrm{289}=\mathrm{17}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}{r}−\mathrm{23}\right)^{\mathrm{2}} =\mathrm{17}^{\mathrm{2}} \\ $$$$\mathrm{2}{r}−\mathrm{23}=\mathrm{17} \\ $$$${r}=\frac{\mathrm{17}+\mathrm{23}}{\mathrm{2}}=\mathrm{20}\:{cm} \\ $$$${area}\:{of}\:{circle}=\pi{r}^{\mathrm{2}} =\mathrm{400}\pi\:{cm}^{\mathrm{2}} \\ $$
Commented by Tawa11 last updated on 08/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
