Question-163610

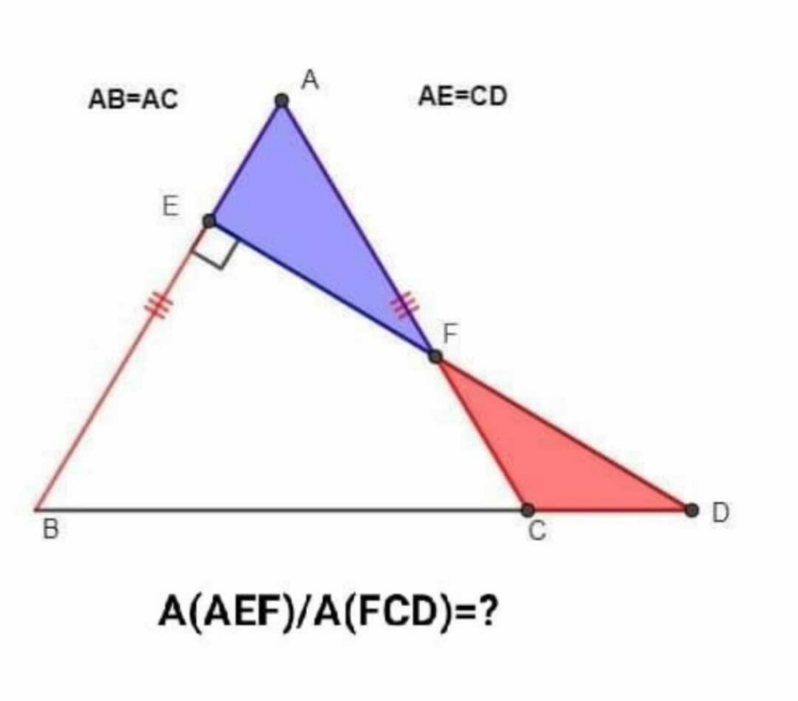
Question Number 163610 by amin96 last updated on 08/Jan/22

Answered by mr W last updated on 08/Jan/22

Commented by mr W last updated on 08/Jan/22

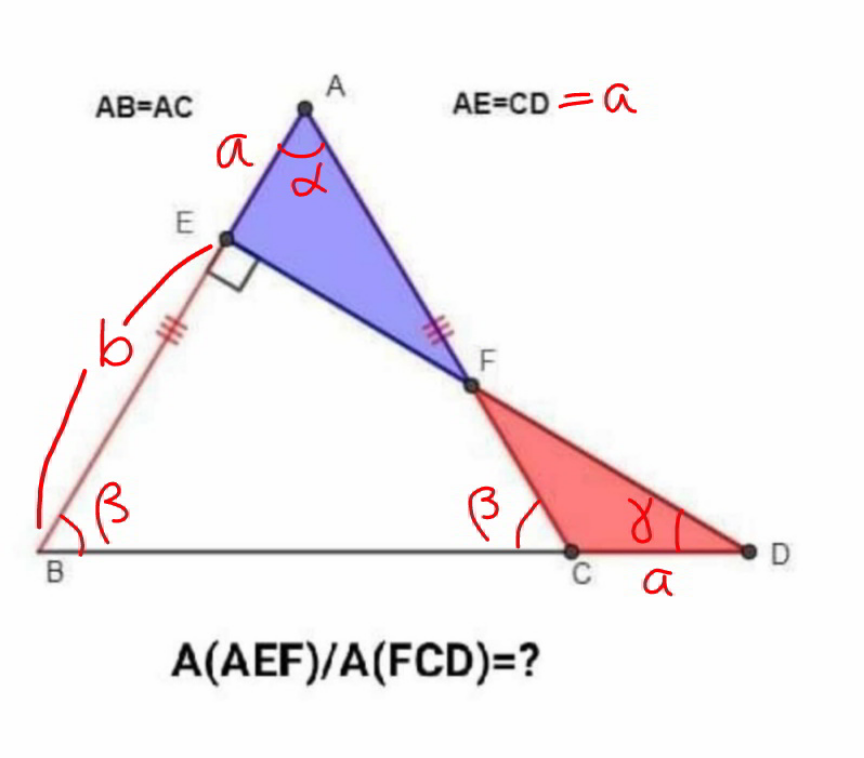
β+(α/2)=90° β+γ=90° ⇒γ=(α/2) BC=2(a+b)sin (α/2) BD=2(a+b)sin (α/2)+a BD×sin γ=(2(a+b)sin (α/2)+a)sin γ=b (1−cos α+sin (α/2))a=b cos α (b/a)=((1−cos α+sin (α/2))/(cos α)) ED=(b/(tan γ)) FD=(b/(tan γ))−a tan α ((FD)/a)=((1−cos α+sin (α/2))/(cos α tan γ))−tan α [AEF]=((a×a tan α)/2) [FCD]=((a×FD sin γ)/2) λ=(([AEF])/([FCD]))=((a tan α)/(FD sin γ)) λ=((tan α)/((((1−cos α+sin (α/2))/(cos α tan γ))−tan α)sin γ)) λ=((tan 2γ)/((((1−cos 2γ+sin γ)/(cos 2γ tan γ))−tan 2γ)sin γ)) λ=(1/((((1−cos 2γ+sin γ)/(sin 2γ tan γ))−1)sin γ)) λ=((sin 2γ)/(2 sin^2 γ cos γ+sin γ cos γ−sin 2γ sin γ)) λ=2 ⇒(([AEF])/([FCD]))=2, independently from the shape of the triangle ABC!

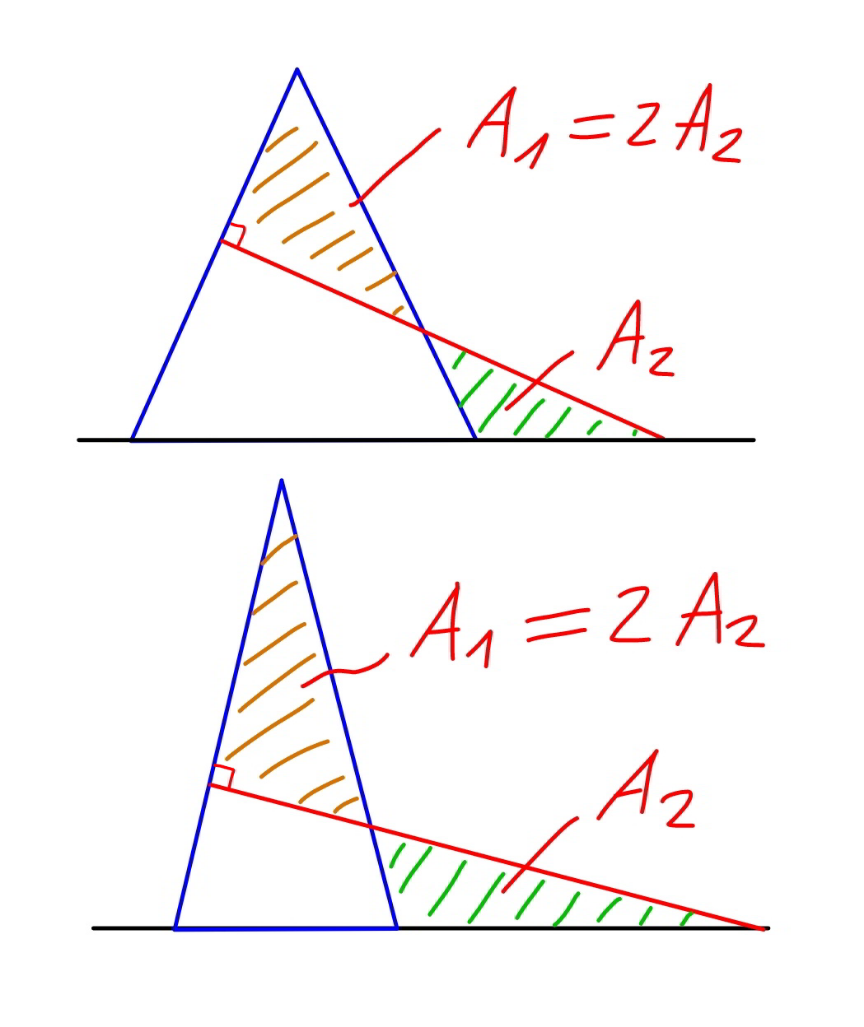
$$\beta+\frac{\alpha}{\mathrm{2}}=\mathrm{90}° \\ $$$$\beta+\gamma=\mathrm{90}° \\ $$$$\Rightarrow\gamma=\frac{\alpha}{\mathrm{2}} \\ $$$${BC}=\mathrm{2}\left({a}+{b}\right)\mathrm{sin}\:\frac{\alpha}{\mathrm{2}} \\ $$$${BD}=\mathrm{2}\left({a}+{b}\right)\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}+{a} \\ $$$${BD}×\mathrm{sin}\:\gamma=\left(\mathrm{2}\left({a}+{b}\right)\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}+{a}\right)\mathrm{sin}\:\gamma={b} \\ $$$$\left(\mathrm{1}−\mathrm{cos}\:\alpha+\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}\right){a}={b}\:\mathrm{cos}\:\alpha \\ $$$$\frac{{b}}{{a}}=\frac{\mathrm{1}−\mathrm{cos}\:\alpha+\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{cos}\:\alpha} \\ $$$${ED}=\frac{{b}}{\mathrm{tan}\:\gamma} \\ $$$${FD}=\frac{{b}}{\mathrm{tan}\:\gamma}−{a}\:\mathrm{tan}\:\alpha \\ $$$$\frac{{FD}}{{a}}=\frac{\mathrm{1}−\mathrm{cos}\:\alpha+\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{cos}\:\alpha\:\mathrm{tan}\:\gamma}−\mathrm{tan}\:\alpha \\ $$$$ \\ $$$$\left[{AEF}\right]=\frac{{a}×{a}\:\mathrm{tan}\:\alpha}{\mathrm{2}} \\ $$$$\left[{FCD}\right]=\frac{{a}×{FD}\:\mathrm{sin}\:\gamma}{\mathrm{2}} \\ $$$$\lambda=\frac{\left[{AEF}\right]}{\left[{FCD}\right]}=\frac{{a}\:\mathrm{tan}\:\alpha}{{FD}\:\mathrm{sin}\:\gamma} \\ $$$$\lambda=\frac{\mathrm{tan}\:\alpha}{\left(\frac{\mathrm{1}−\mathrm{cos}\:\alpha+\mathrm{sin}\:\frac{\alpha}{\mathrm{2}}}{\mathrm{cos}\:\alpha\:\mathrm{tan}\:\gamma}−\mathrm{tan}\:\alpha\right)\mathrm{sin}\:\gamma} \\ $$$$\lambda=\frac{\mathrm{tan}\:\mathrm{2}\gamma}{\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\gamma+\mathrm{sin}\:\gamma}{\mathrm{cos}\:\mathrm{2}\gamma\:\mathrm{tan}\:\gamma}−\mathrm{tan}\:\mathrm{2}\gamma\right)\mathrm{sin}\:\gamma} \\ $$$$\lambda=\frac{\mathrm{1}}{\left(\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}\gamma+\mathrm{sin}\:\gamma}{\mathrm{sin}\:\mathrm{2}\gamma\:\mathrm{tan}\:\gamma}−\mathrm{1}\right)\mathrm{sin}\:\gamma} \\ $$$$\lambda=\frac{\mathrm{sin}\:\mathrm{2}\gamma}{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\gamma\:\mathrm{cos}\:\gamma+\mathrm{sin}\:\gamma\:\mathrm{cos}\:\gamma−\mathrm{sin}\:\mathrm{2}\gamma\:\mathrm{sin}\:\gamma} \\ $$$$\lambda=\mathrm{2} \\ $$$$\Rightarrow\frac{\left[{AEF}\right]}{\left[{FCD}\right]}=\mathrm{2},\:{independently}\:{from}\:{the} \\ $$$${shape}\:{of}\:{the}\:{triangle}\:{ABC}! \\ $$

Commented by mr W last updated on 08/Jan/22