Question-163624

Question Number 163624 by amin96 last updated on 08/Jan/22

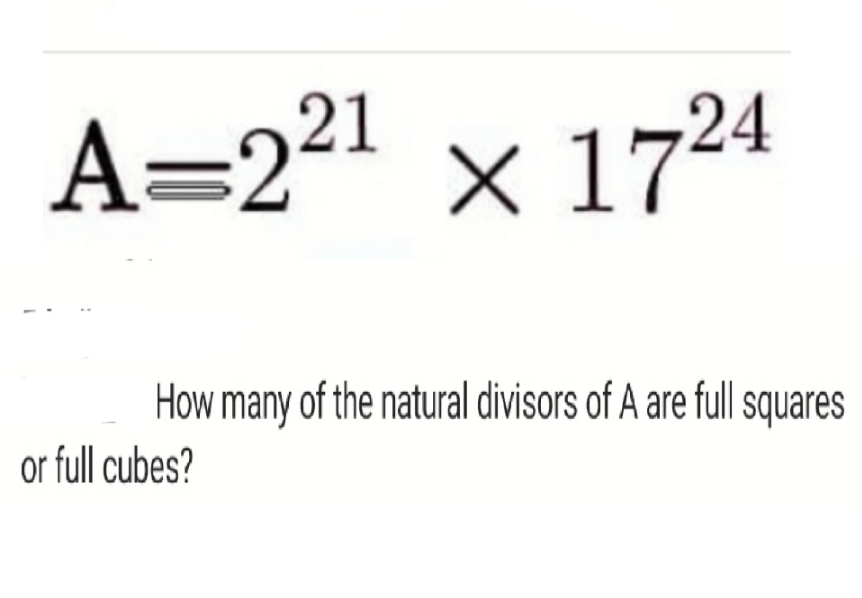
Answered by mr W last updated on 09/Jan/22

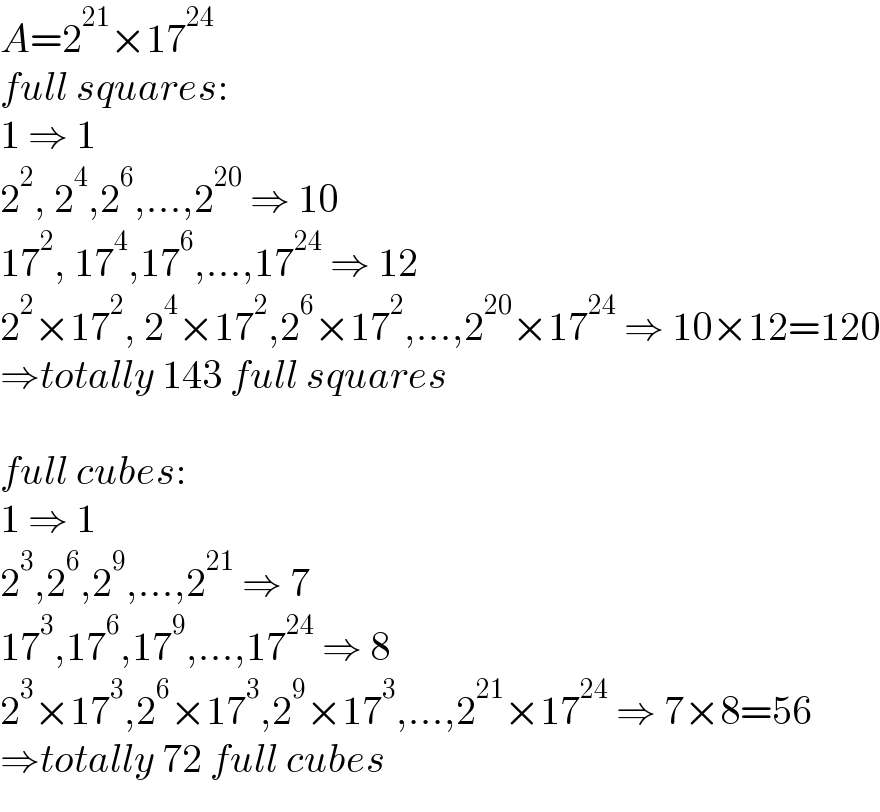
A=2^(21) ×17^(24) full squares: 1 ⇒ 1 2^2 , 2^4 ,2^6 ,...,2^(20) ⇒ 10 17^2 , 17^4 ,17^6 ,...,17^(24) ⇒ 12 2^2 ×17^2 , 2^4 ×17^2 ,2^6 ×17^2 ,...,2^(20) ×17^(24) ⇒ 10×12=120 ⇒totally 143 full squares full cubes: 1 ⇒ 1 2^3 ,2^6 ,2^9 ,...,2^(21) ⇒ 7 17^3 ,17^6 ,17^9 ,...,17^(24) ⇒ 8 2^3 ×17^3 ,2^6 ×17^3 ,2^9 ×17^3 ,...,2^(21) ×17^(24) ⇒ 7×8=56 ⇒totally 72 full cubes

$${A}=\mathrm{2}^{\mathrm{21}} ×\mathrm{17}^{\mathrm{24}} \\ $$$${full}\:{squares}: \\ $$$$\mathrm{1}\:\Rightarrow\:\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{2}} ,\:\mathrm{2}^{\mathrm{4}} ,\mathrm{2}^{\mathrm{6}} ,…,\mathrm{2}^{\mathrm{20}} \:\Rightarrow\:\mathrm{10} \\ $$$$\mathrm{17}^{\mathrm{2}} ,\:\mathrm{17}^{\mathrm{4}} ,\mathrm{17}^{\mathrm{6}} ,…,\mathrm{17}^{\mathrm{24}} \:\Rightarrow\:\mathrm{12} \\ $$$$\mathrm{2}^{\mathrm{2}} ×\mathrm{17}^{\mathrm{2}} ,\:\mathrm{2}^{\mathrm{4}} ×\mathrm{17}^{\mathrm{2}} ,\mathrm{2}^{\mathrm{6}} ×\mathrm{17}^{\mathrm{2}} ,…,\mathrm{2}^{\mathrm{20}} ×\mathrm{17}^{\mathrm{24}} \:\Rightarrow\:\mathrm{10}×\mathrm{12}=\mathrm{120} \\ $$$$\Rightarrow{totally}\:\mathrm{143}\:{full}\:{squares} \\ $$$$ \\ $$$${full}\:{cubes}: \\ $$$$\mathrm{1}\:\Rightarrow\:\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{3}} ,\mathrm{2}^{\mathrm{6}} ,\mathrm{2}^{\mathrm{9}} ,…,\mathrm{2}^{\mathrm{21}} \:\Rightarrow\:\mathrm{7} \\ $$$$\mathrm{17}^{\mathrm{3}} ,\mathrm{17}^{\mathrm{6}} ,\mathrm{17}^{\mathrm{9}} ,…,\mathrm{17}^{\mathrm{24}} \:\Rightarrow\:\mathrm{8} \\ $$$$\mathrm{2}^{\mathrm{3}} ×\mathrm{17}^{\mathrm{3}} ,\mathrm{2}^{\mathrm{6}} ×\mathrm{17}^{\mathrm{3}} ,\mathrm{2}^{\mathrm{9}} ×\mathrm{17}^{\mathrm{3}} ,…,\mathrm{2}^{\mathrm{21}} ×\mathrm{17}^{\mathrm{24}} \:\Rightarrow\:\mathrm{7}×\mathrm{8}=\mathrm{56} \\ $$$$\Rightarrow{totally}\:\mathrm{72}\:{full}\:{cubes} \\ $$

Commented by mr W last updated on 09/Jan/22

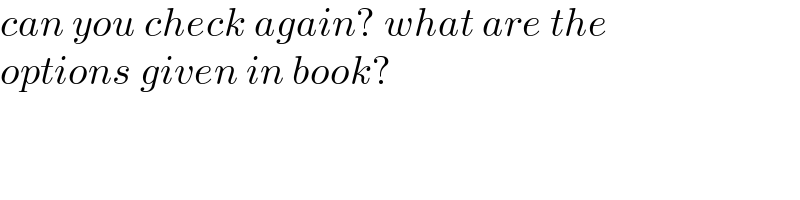
$${can}\:{you}\:{check}\:{again}?\:{what}\:{are}\:{the} \\ $$$${options}\:{given}\:{in}\:{book}? \\ $$

Commented by amin96 last updated on 09/Jan/22

$${great}\:{sir}\:{correct} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply