Menu Close

Question-163763

Tinku Tara 0 Comments
Pin




Question Number 163763 by Rasheed.Sindhi last updated on 10/Jan/22
$$ \\ $$
Commented by Rasheed.Sindhi last updated on 10/Jan/22
Q#163397 reposted
$${Q}#\mathrm{163397}\:{reposted} \\ $$
Answered by Rasheed.Sindhi last updated on 10/Jan/22
II.)Determine the set couple a,b∈N^∗ such as LCM(a,b)+GCD(a,b)=b+9 _(−) GCD(a,b)=d⇒LCM(a,b)=((ab)/d) ((ab)/d)+d=b+9 b((a/d)−1)=9−d d=1,2,3,...,8 Case:d=1: ab+1=b+9 ab−b=8 b(a−1)=8=1×8=8×1=2×4=4×2 b=1,a=9 ✓ b=4,a=3✓ b=2,a=5✓ Case:d=2⇒a,b≥2 b((a/2)−1)=9−2=7=1×7=7×1 b=7, (a/2)−1=1⇒a=4 [GCD(4,7)≠2]] Case:d=3⇒a,b≥3 b((a/3)−1)=9−3=6=3×2 b=3,(a/3)−1=2⇒a=9✓ Case:d=4⇒a,b≥4 b((a/4)−1)=9−4=5=5×1 b=5,(a/4)−1=1⇒a=8 [GCD(5,8)≠4] Case:d=5⇒a,b≥5 b((a/5)−1)=9−5=4 [No value of a,b≥5] Cases:d≥5⇒a,b≥d [No value of a,b≥d] (a,b)=(9,1),(3,4),(5,2),(9,3)
$$ \\ $$$$\left.\mathrm{II}.\right){Determine}\:{the}\:{set}\:{couple} \\ $$$${a},{b}\in\mathbb{N}^{\ast} \:{such}\:{as} \\ $$$$\underset{−} {\mathrm{LCM}\left({a},{b}\right)+\mathrm{GCD}\left({a},{b}\right)={b}+\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:} \\ $$$$\:\mathrm{GCD}\left({a},{b}\right)={d}\Rightarrow\mathrm{LCM}\left({a},{b}\right)=\frac{{ab}}{{d}} \\ $$$$\:\:\:\:\:\frac{{ab}}{{d}}+{d}={b}+\mathrm{9} \\ $$$$\:\:\:\:\:{b}\left(\frac{{a}}{{d}}−\mathrm{1}\right)=\mathrm{9}−{d} \\ $$$$\:{d}=\mathrm{1},\mathrm{2},\mathrm{3},…,\mathrm{8} \\ $$$${Case}:{d}=\mathrm{1}:\:{ab}+\mathrm{1}={b}+\mathrm{9} \\ $$$$\:\:\:{ab}−{b}=\mathrm{8} \\ $$$$\:\:{b}\left({a}−\mathrm{1}\right)=\mathrm{8}=\mathrm{1}×\mathrm{8}=\mathrm{8}×\mathrm{1}=\mathrm{2}×\mathrm{4}=\mathrm{4}×\mathrm{2} \\ $$$${b}=\mathrm{1},{a}=\mathrm{9}\:\checkmark \\ $$$${b}=\mathrm{4},{a}=\mathrm{3}\checkmark\: \\ $$$${b}=\mathrm{2},{a}=\mathrm{5}\checkmark \\ $$$${Case}:{d}=\mathrm{2}\Rightarrow{a},{b}\geqslant\mathrm{2} \\ $$$$\:{b}\left(\frac{{a}}{\mathrm{2}}−\mathrm{1}\right)=\mathrm{9}−\mathrm{2}=\mathrm{7}=\mathrm{1}×\mathrm{7}=\mathrm{7}×\mathrm{1} \\ $$$$\left.{b}=\mathrm{7},\:\frac{{a}}{\mathrm{2}}−\mathrm{1}=\mathrm{1}\Rightarrow{a}=\mathrm{4}\:\left[\mathrm{GCD}\left(\mathrm{4},\mathrm{7}\right)\neq\mathrm{2}\right]\right] \\ $$$${Case}:{d}=\mathrm{3}\Rightarrow{a},{b}\geqslant\mathrm{3} \\ $$$${b}\left(\frac{{a}}{\mathrm{3}}−\mathrm{1}\right)=\mathrm{9}−\mathrm{3}=\mathrm{6}=\mathrm{3}×\mathrm{2} \\ $$$${b}=\mathrm{3},\frac{{a}}{\mathrm{3}}−\mathrm{1}=\mathrm{2}\Rightarrow{a}=\mathrm{9}\checkmark \\ $$$${Case}:{d}=\mathrm{4}\Rightarrow{a},{b}\geqslant\mathrm{4} \\ $$$${b}\left(\frac{{a}}{\mathrm{4}}−\mathrm{1}\right)=\mathrm{9}−\mathrm{4}=\mathrm{5}=\mathrm{5}×\mathrm{1} \\ $$$${b}=\mathrm{5},\frac{{a}}{\mathrm{4}}−\mathrm{1}=\mathrm{1}\Rightarrow{a}=\mathrm{8}\:\left[\mathrm{GCD}\left(\mathrm{5},\mathrm{8}\right)\neq\mathrm{4}\right] \\ $$$${Case}:{d}=\mathrm{5}\Rightarrow{a},{b}\geqslant\mathrm{5} \\ $$$${b}\left(\frac{{a}}{\mathrm{5}}−\mathrm{1}\right)=\mathrm{9}−\mathrm{5}=\mathrm{4}\:\left[{No}\:{value}\:{of}\:{a},{b}\geqslant\mathrm{5}\right] \\ $$$${Cases}:{d}\geqslant\mathrm{5}\Rightarrow{a},{b}\geqslant{d}\:\left[{No}\:{value}\:{of}\:{a},{b}\geqslant{d}\right] \\ $$$$\left({a},{b}\right)=\left(\mathrm{9},\mathrm{1}\right),\left(\mathrm{3},\mathrm{4}\right),\left(\mathrm{5},\mathrm{2}\right),\left(\mathrm{9},\mathrm{3}\right) \\ $$
Answered by Rasheed.Sindhi last updated on 10/Jan/22
III.) Dividend=a,Divisor=b,Remainder=r<b Quotient=q These quantities are related as under: a=bq+r ; 0≤r<b r=25 ∧ b>r⇒b>25 ∴Minimum value of b=26 a=bq+r⇒a=26×17+25 a=467 (a,b)=(467,26)
$$ \\ $$$$\left.\mathrm{III}.\right) \\ $$$$\mathcal{D}{ividend}={a},\mathcal{D}{ivisor}={b},{Remainder}={r}<{b} \\ $$$$\mathcal{Q}{uotient}={q} \\ $$$$\mathcal{T}{hese}\:{quantities}\:{are}\:{related}\:{as}\:{under}: \\ $$$$\:\:\:{a}={bq}+{r}\:;\:\mathrm{0}\leqslant{r}<{b} \\ $$$${r}=\mathrm{25}\:\wedge\:{b}>{r}\Rightarrow{b}>\mathrm{25} \\ $$$$\therefore{Minimum}\:{value}\:{of}\:{b}=\mathrm{26} \\ $$$$\:{a}={bq}+{r}\Rightarrow{a}=\mathrm{26}×\mathrm{17}+\mathrm{25} \\ $$$${a}=\mathrm{467} \\ $$$$\left({a},{b}\right)=\left(\mathrm{467},\mathrm{26}\right) \\ $$
Answered by kdaramaths last updated on 10/Jan/22
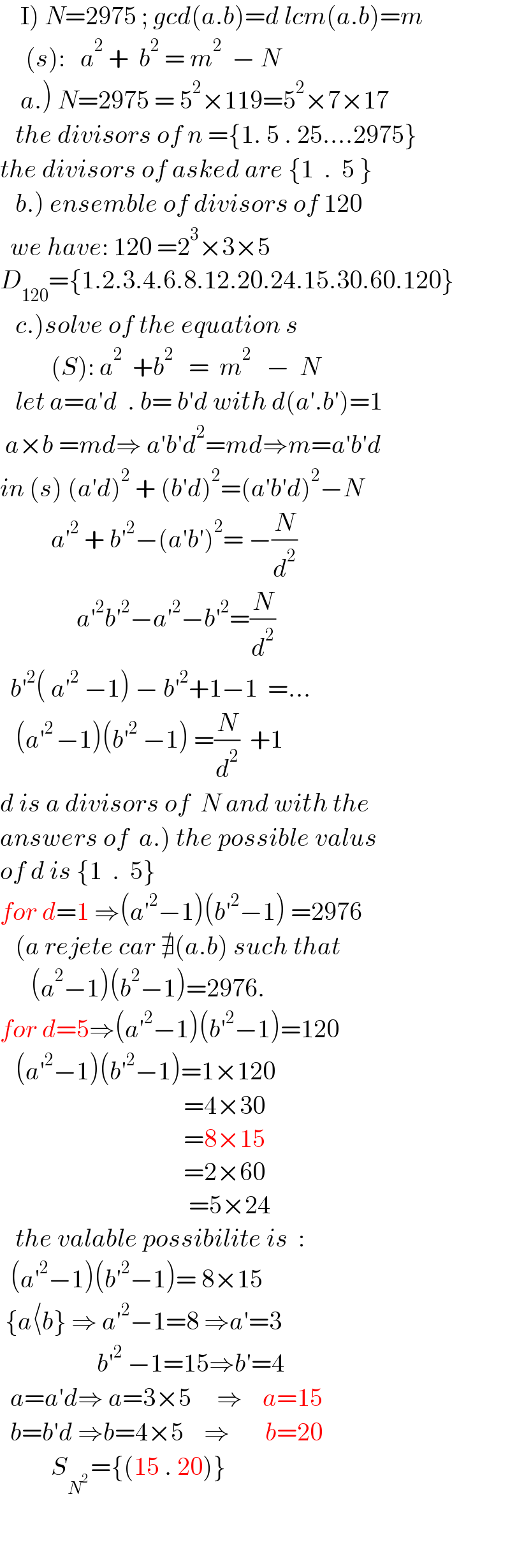
I) N=2975 ; gcd(a.b)=d lcm(a.b)=m (s): a^2 + b^2 = m^2 − N a.) N=2975 = 5^2 ×119=5^2 ×7×17 the divisors of n ={1. 5 . 25....2975} the divisors of asked are {1 . 5 } b.) ensemble of divisors of 120 we have: 120 =2^3 ×3×5 D_(120) ={1.2.3.4.6.8.12.20.24.15.30.60.120} c.)solve of the equation s (S): a^2 +b^2 = m^2 − N let a=a′d . b= b′d with d(a′.b′)=1 a×b =md⇒ a′b′d^2 =md⇒m=a′b′d in (s) (a′d)^2 + (b′d)^2 =(a′b′d)^2 −N a′^2 + b′^2 −(a′b′)^2 = −(N/d^2 ) a′^2 b′^2 −a′^2 −b′^2 =(N/d^2 ) b′^2 ( a′^2 −1) − b′^2 +1−1 =... (a′^(2 ) −1)(b′^2 −1) =(N/d^2 ) +1 d is a divisors of N and with the answers of a.) the possible valus of d is {1 . 5} for d=1 ⇒(a′^2 −1)(b′^2 −1) =2976 (a rejete car ∄(a.b) such that (a^2 −1)(b^2 −1)=2976. for d=5⇒(a′^2 −1)(b′^2 −1)=120 (a′^2 −1)(b′^2 −1)=1×120 =4×30 =8×15 =2×60 =5×24 the valable possibilite is : (a′^2 −1)(b′^2 −1)= 8×15 {a⟨b} ⇒ a′^2 −1=8 ⇒a′=3 b′^2 −1=15⇒b′=4 a=a′d⇒ a=3×5 ⇒ a=15 b=b′d ⇒b=4×5 ⇒ b=20 S_N^(2 ) ={(15 . 20)}
$$\left.\:\:\:\:\mathrm{I}\right)\:{N}=\mathrm{2975}\:;\:{gcd}\left({a}.{b}\right)={d}\:{lcm}\left({a}.{b}\right)={m} \\ $$$$\:\:\:\:\:\left({s}\right):\:\:\:{a}^{\mathrm{2}} \:+\:\:{b}^{\mathrm{2}} \:=\:{m}^{\mathrm{2}} \:\:−\:{N} \\ $$$$\left.\:\:\:\:{a}.\right)\:{N}=\mathrm{2975}\:=\:\mathrm{5}^{\mathrm{2}} ×\mathrm{119}=\mathrm{5}^{\mathrm{2}} ×\mathrm{7}×\mathrm{17} \\ $$$$\:\:\:{the}\:{divisors}\:{of}\:{n}\:=\left\{\mathrm{1}.\:\mathrm{5}\:.\:\mathrm{25}….\mathrm{2975}\right\} \\ $$$${the}\:{divisors}\:{of}\:{asked}\:{are}\:\left\{\mathrm{1}\:\:.\:\:\mathrm{5}\:\right\} \\ $$$$\left.\:\:\:{b}.\right)\:{ensemble}\:{of}\:{divisors}\:{of}\:\mathrm{120} \\ $$$$\:\:{we}\:{have}:\:\mathrm{120}\:=\mathrm{2}^{\mathrm{3}} ×\mathrm{3}×\mathrm{5} \\ $$$${D}_{\mathrm{120}} =\left\{\mathrm{1}.\mathrm{2}.\mathrm{3}.\mathrm{4}.\mathrm{6}.\mathrm{8}.\mathrm{12}.\mathrm{20}.\mathrm{24}.\mathrm{15}.\mathrm{30}.\mathrm{60}.\mathrm{120}\right\} \\ $$$$\left.\:\:\:{c}.\right){solve}\:{of}\:{the}\:{equation}\:{s} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left({S}\right):\:{a}^{\mathrm{2}} \:\:+{b}^{\mathrm{2}} \:\:\:=\:\:{m}^{\mathrm{2}} \:\:\:−\:\:{N} \\ $$$$\:\:\:{let}\:{a}={a}'{d}\:\:.\:{b}=\:{b}'{d}\:{with}\:{d}\left({a}'.{b}'\right)=\mathrm{1} \\ $$$$\:{a}×{b}\:={md}\Rightarrow\:{a}'{b}'{d}^{\mathrm{2}} ={md}\Rightarrow{m}={a}'{b}'{d} \\ $$$${in}\:\left({s}\right)\:\left({a}'{d}\right)^{\mathrm{2}} \:+\:\left({b}'{d}\right)^{\mathrm{2}} =\left({a}'{b}'{d}\right)^{\mathrm{2}} −{N} \\ $$$$\:\:\:\:\:\:\:\:\:\:{a}'^{\mathrm{2}} \:+\:{b}'^{\mathrm{2}} −\left({a}'{b}'\right)^{\mathrm{2}} =\:−\frac{{N}}{{d}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{a}'^{\mathrm{2}} {b}'^{\mathrm{2}} −{a}'^{\mathrm{2}} −{b}'^{\mathrm{2}} =\frac{{N}}{{d}^{\mathrm{2}} } \\ $$$$\:\:{b}'^{\mathrm{2}} \left(\:{a}'^{\mathrm{2}} \:−\mathrm{1}\right)\:−\:{b}'^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\:\:=… \\ $$$$\:\:\:\left({a}'^{\mathrm{2}\:} −\mathrm{1}\right)\left({b}'^{\mathrm{2}} \:−\mathrm{1}\right)\:=\frac{{N}}{{d}^{\mathrm{2}} }\:\:+\mathrm{1} \\ $$$${d}\:{is}\:{a}\:{divisors}\:{of}\:\:{N}\:{and}\:{with}\:{the}\: \\ $$$$\left.{answers}\:{of}\:\:{a}.\right)\:{the}\:{possible}\:{valus}\: \\ $$$${of}\:{d}\:{is}\:\left\{\mathrm{1}\:\:.\:\:\mathrm{5}\right\} \\ $$$${for}\:{d}=\mathrm{1}\:\Rightarrow\left({a}'^{\mathrm{2}} −\mathrm{1}\right)\left({b}'^{\mathrm{2}} −\mathrm{1}\right)\:=\mathrm{2976} \\ $$$$\:\:\:\left({a}\:{rejete}\:{car}\:\nexists\left({a}.{b}\right)\:{such}\:{that}\:\right. \\ $$$$\:\:\:\:\:\:\left({a}^{\mathrm{2}} −\mathrm{1}\right)\left({b}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{2976}. \\ $$$${for}\:{d}=\mathrm{5}\Rightarrow\left({a}'^{\mathrm{2}} −\mathrm{1}\right)\left({b}'^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{120} \\ $$$$\:\:\:\left({a}'^{\mathrm{2}} −\mathrm{1}\right)\left({b}'^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{1}×\mathrm{120} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{4}×\mathrm{30} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8}×\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}×\mathrm{60} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}×\mathrm{24} \\ $$$$\:\:\:{the}\:{valable}\:{possibilite}\:{is}\:\:: \\ $$$$\:\:\left({a}'^{\mathrm{2}} −\mathrm{1}\right)\left({b}'^{\mathrm{2}} −\mathrm{1}\right)=\:\mathrm{8}×\mathrm{15}\:\: \\ $$$$\:\left\{{a}\langle{b}\right\}\:\Rightarrow\:{a}'^{\mathrm{2}} −\mathrm{1}=\mathrm{8}\:\Rightarrow{a}'=\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{b}'^{\mathrm{2}} \:−\mathrm{1}=\mathrm{15}\Rightarrow{b}'=\mathrm{4} \\ $$$$\:\:{a}={a}'{d}\Rightarrow\:{a}=\mathrm{3}×\mathrm{5}\:\:\:\:\:\Rightarrow\:\:\:\:{a}=\mathrm{15} \\ $$$$\:\:{b}={b}'{d}\:\Rightarrow{b}=\mathrm{4}×\mathrm{5}\:\:\:\:\Rightarrow\:\:\:\:\:\:\:{b}=\mathrm{20} \\ $$$$\:\:\:\:\:\:\:\:\:\:{S}_{{N}^{\mathrm{2}\:} } =\left\{\left(\mathrm{15}\:.\:\mathrm{20}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *