Question Number 163782 by bekzodjumayev last updated on 10/Jan/22

Commented by bekzodjumayev last updated on 10/Jan/22

$${Please}\:{help} \\ $$
Answered by Ar Brandon last updated on 10/Jan/22
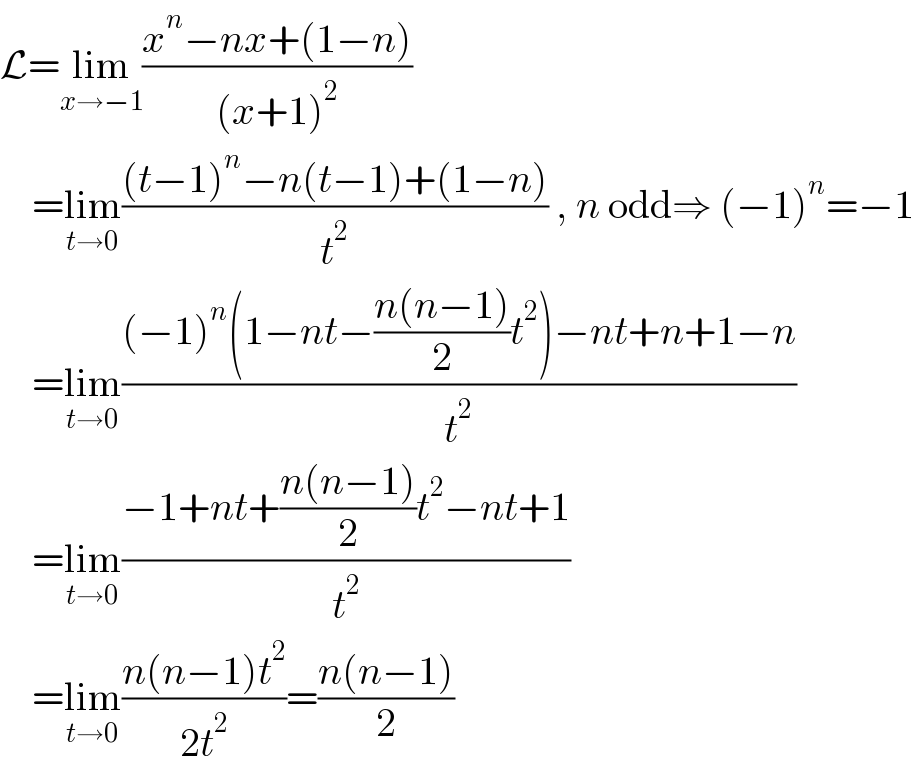
$$\mathcal{L}=\underset{{x}\rightarrow−\mathrm{1}} {\mathrm{lim}}\frac{{x}^{{n}} −{nx}+\left(\mathrm{1}−{n}\right)}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left({t}−\mathrm{1}\right)^{{n}} −{n}\left({t}−\mathrm{1}\right)+\left(\mathrm{1}−{n}\right)}{{t}^{\mathrm{2}} }\:,\:{n}\:\mathrm{odd}\Rightarrow\:\left(−\mathrm{1}\right)^{{n}} =−\mathrm{1} \\ $$$$\:\:\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{1}−{nt}−\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} \right)−{nt}+{n}+\mathrm{1}−{n}}{{t}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{−\mathrm{1}+{nt}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}}{t}^{\mathrm{2}} −{nt}+\mathrm{1}}{{t}^{\mathrm{2}} } \\ $$$$\:\:\:\:=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{n}\left({n}−\mathrm{1}\right){t}^{\mathrm{2}} }{\mathrm{2}{t}^{\mathrm{2}} }=\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by bekzodjumayev last updated on 11/Jan/22

$${Thank}\:{you} \\ $$
