Question Number 163786 by mnjuly1970 last updated on 10/Jan/22
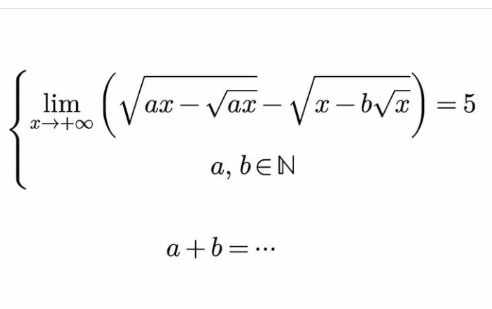
Answered by cortano1 last updated on 11/Jan/22
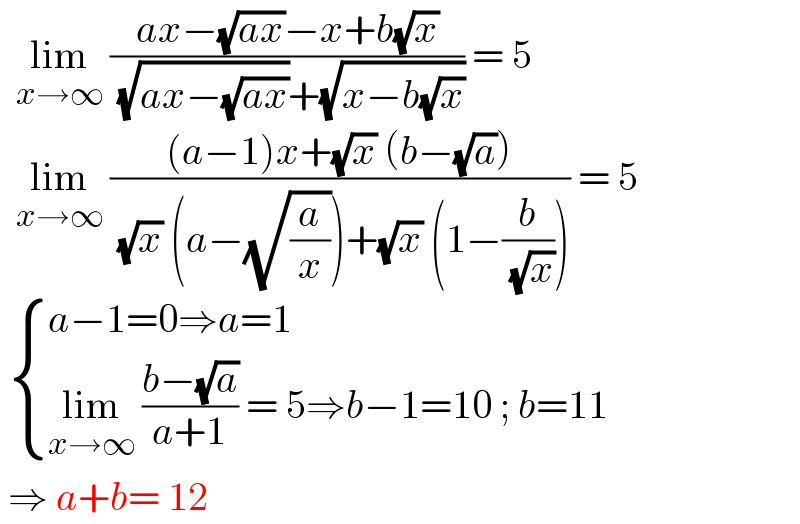
$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{ax}−\sqrt{{ax}}−{x}+{b}\sqrt{{x}}}{\:\sqrt{{ax}−\sqrt{{ax}}}+\sqrt{{x}−{b}\sqrt{{x}}}}\:=\:\mathrm{5} \\ $$$$\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\left({a}−\mathrm{1}\right){x}+\sqrt{{x}}\:\left({b}−\sqrt{{a}}\right)}{\:\sqrt{{x}}\:\left({a}−\sqrt{\frac{{a}}{{x}}}\right)+\sqrt{{x}}\:\left(\mathrm{1}−\frac{{b}}{\:\sqrt{{x}}}\right)}\:=\:\mathrm{5} \\ $$$$\:\begin{cases}{{a}−\mathrm{1}=\mathrm{0}\Rightarrow{a}=\mathrm{1}}\\{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{{b}−\sqrt{{a}}}{{a}+\mathrm{1}}\:=\:\mathrm{5}\Rightarrow{b}−\mathrm{1}=\mathrm{10}\:;\:{b}=\mathrm{11}}\end{cases} \\ $$$$\:\Rightarrow\:{a}+{b}=\:\mathrm{12} \\ $$
Commented by mnjuly1970 last updated on 11/Jan/22

$${greateful}\:{sir}.. \\ $$
