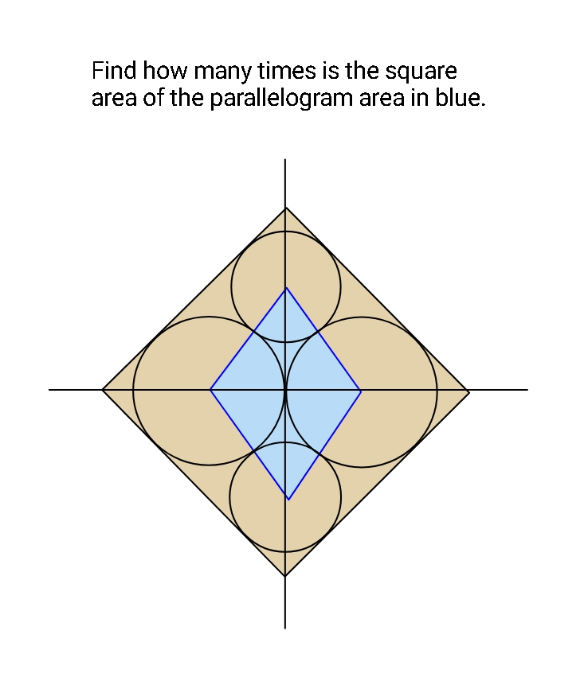
Question Number 163921 by ajfour last updated on 11/Jan/22
Answered by mr W last updated on 12/Jan/22
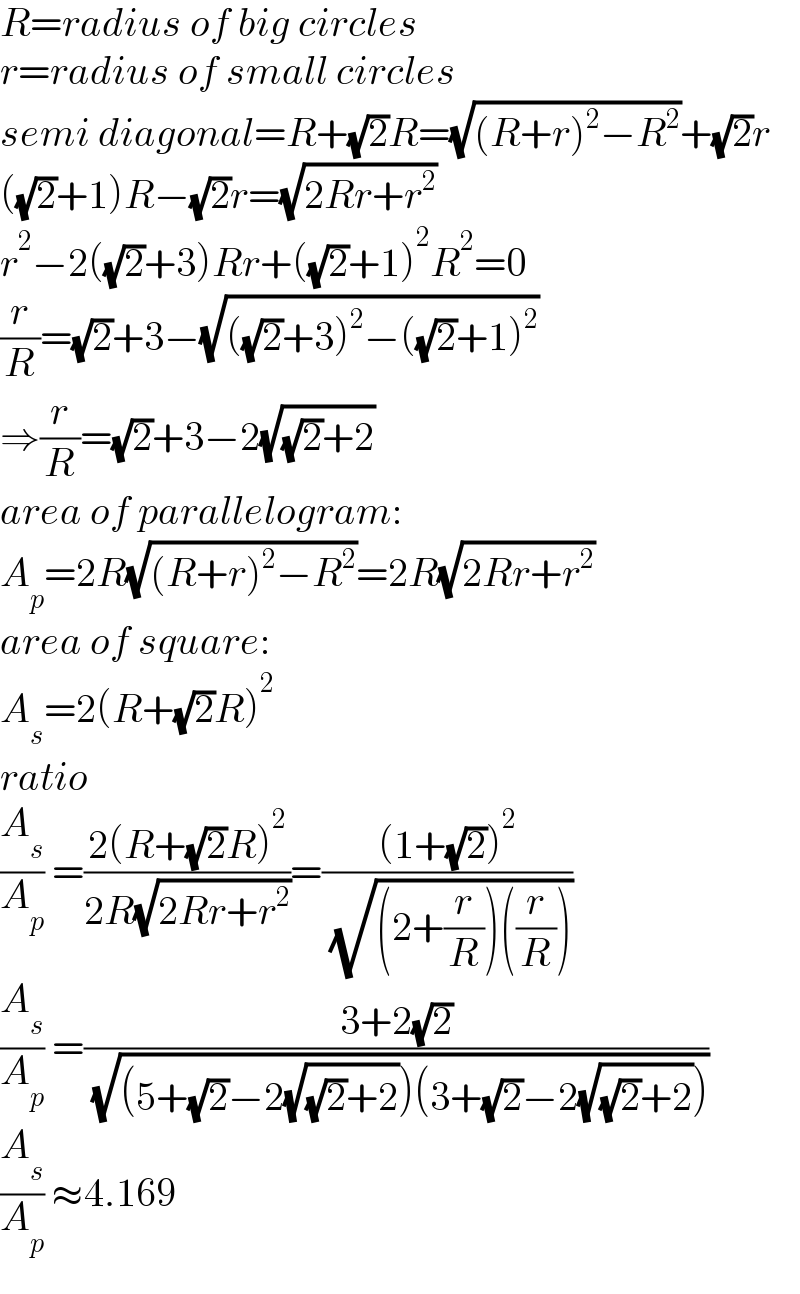
$${R}={radius}\:{of}\:{big}\:{circles} \\ $$$${r}={radius}\:{of}\:{small}\:{circles} \\ $$$${semi}\:{diagonal}={R}+\sqrt{\mathrm{2}}{R}=\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }+\sqrt{\mathrm{2}}{r} \\ $$$$\left(\sqrt{\mathrm{2}}+\mathrm{1}\right){R}−\sqrt{\mathrm{2}}{r}=\sqrt{\mathrm{2}{Rr}+{r}^{\mathrm{2}} } \\ $$$${r}^{\mathrm{2}} −\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{3}\right){Rr}+\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} {R}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{r}}{{R}}=\sqrt{\mathrm{2}}+\mathrm{3}−\sqrt{\left(\sqrt{\mathrm{2}}+\mathrm{3}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{r}}{{R}}=\sqrt{\mathrm{2}}+\mathrm{3}−\mathrm{2}\sqrt{\sqrt{\mathrm{2}}+\mathrm{2}} \\ $$$${area}\:{of}\:{parallelogram}: \\ $$$${A}_{{p}} =\mathrm{2}{R}\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }=\mathrm{2}{R}\sqrt{\mathrm{2}{Rr}+{r}^{\mathrm{2}} } \\ $$$${area}\:{of}\:{square}: \\ $$$${A}_{{s}} =\mathrm{2}\left({R}+\sqrt{\mathrm{2}}{R}\right)^{\mathrm{2}} \\ $$$${ratio} \\ $$$$\frac{{A}_{{s}} }{{A}_{{p}} }\:=\frac{\mathrm{2}\left({R}+\sqrt{\mathrm{2}}{R}\right)^{\mathrm{2}} }{\mathrm{2}{R}\sqrt{\mathrm{2}{Rr}+{r}^{\mathrm{2}} }}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }{\:\sqrt{\left(\mathrm{2}+\frac{{r}}{{R}}\right)\left(\frac{{r}}{{R}}\right)}} \\ $$$$\frac{{A}_{{s}} }{{A}_{{p}} }\:=\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}{\:\sqrt{\left(\mathrm{5}+\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\sqrt{\mathrm{2}}+\mathrm{2}}\right)\left(\mathrm{3}+\sqrt{\mathrm{2}}−\mathrm{2}\sqrt{\sqrt{\mathrm{2}}+\mathrm{2}}\right)}} \\ $$$$\frac{{A}_{{s}} }{{A}_{{p}} }\:\approx\mathrm{4}.\mathrm{169} \\ $$
Commented by Tawa11 last updated on 12/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 12/Jan/22
![R+R(√2)=s(√2) R+r+2(√(Rr))=2s (√(r/R))+1=(√((2s)/R)) R=(2−(√2))s r=R((√(2/(2−(√2))))−1)^2 =R((√(2+(√2)))−1)^2 A_p =4R(√((r+R)^2 −R^2 )) =(4s^2 )(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) (A_p /A_s )=(2−(√2))^2 {[((√(2+(√2)))−1)^2 +1]^2 −1}^(1/2) ...](https://www.tinkutara.com/question/Q164000.png)
$${R}+{R}\sqrt{\mathrm{2}}={s}\sqrt{\mathrm{2}} \\ $$$${R}+{r}+\mathrm{2}\sqrt{{Rr}}=\mathrm{2}{s} \\ $$$$\sqrt{\frac{{r}}{{R}}}+\mathrm{1}=\sqrt{\frac{\mathrm{2}{s}}{{R}}} \\ $$$${R}=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){s} \\ $$$${r}={R}\left(\sqrt{\frac{\mathrm{2}}{\mathrm{2}−\sqrt{\mathrm{2}}}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\:\:\:={R}\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$${A}_{{p}} =\mathrm{4}{R}\sqrt{\left({r}+{R}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\left(\mathrm{4}{s}^{\mathrm{2}} \right)\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left\{\left[\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right]^{\mathrm{2}} −\mathrm{1}\right\}^{\mathrm{1}/\mathrm{2}} \\ $$$$\frac{{A}_{{p}} }{{A}_{{s}} }=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \left\{\left[\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{1}\right]^{\mathrm{2}} −\mathrm{1}\right\}^{\mathrm{1}/\mathrm{2}} \\ $$$$… \\ $$
