Question Number 163954 by mnjuly1970 last updated on 12/Jan/22
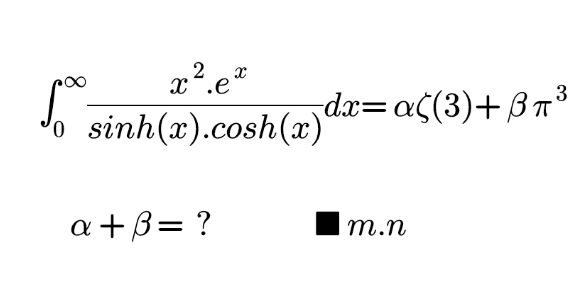
Answered by mathmax by abdo last updated on 13/Jan/22

$$\Psi=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{2}} \:\mathrm{e}^{\mathrm{x}} }{\mathrm{sh}\left(\mathrm{2x}\right)}\mathrm{dx}\:=_{\mathrm{2x}=\mathrm{t}} \:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{2}}} }{\mathrm{4sh}\left(\mathrm{t}\right)}\frac{\mathrm{dt}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{2}\:} \mathrm{e}^{\frac{\mathrm{t}}{\mathrm{2}}} }{\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{2}} \mathrm{e}^{\frac{\mathrm{t}}{\mathrm{2}}} }{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\mathrm{2}} \mathrm{e}^{−\mathrm{t}+\frac{\mathrm{t}}{\mathrm{2}}} }{\mathrm{1}−\mathrm{e}^{−\mathrm{2t}} }\mathrm{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}\:} \:\mathrm{e}^{−\frac{\mathrm{t}}{\mathrm{2}}} \:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \:\mathrm{e}^{−\mathrm{2nt}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}\:} \:\mathrm{e}^{−\frac{\mathrm{t}}{\mathrm{2}}−\mathrm{2nt}} \:\mathrm{dt} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{e}^{−\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{t}} \:\mathrm{dt}\:=_{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{t}=\mathrm{z}} \:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{z}^{\mathrm{2}} }{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:}\:\mathrm{e}^{−\mathrm{z}} \:\frac{\mathrm{dz}}{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }\int_{\mathrm{0}} ^{\infty} \:\mathrm{z}^{\mathrm{2}} \:\mathrm{e}^{−\mathrm{z}} \mathrm{dz}\:=\frac{\Gamma\left(\mathrm{3}\right)}{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\Psi=\frac{\mathrm{2}!}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{2n}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }=\mathrm{8}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{4n}+\mathrm{1}\right)^{\mathrm{3}} }=\frac{\mathrm{8}}{\mathrm{4}^{\mathrm{3}} }\sum_{\mathrm{n}=\mathrm{0}} ^{\infty\:} \frac{\mathrm{1}}{\left(\mathrm{n}+\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} } \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{this}\:\mathrm{sum}\:\mathrm{using}\:\mathrm{digamma}\:\mathrm{function}…. \\ $$
Answered by Lordose last updated on 13/Jan/22
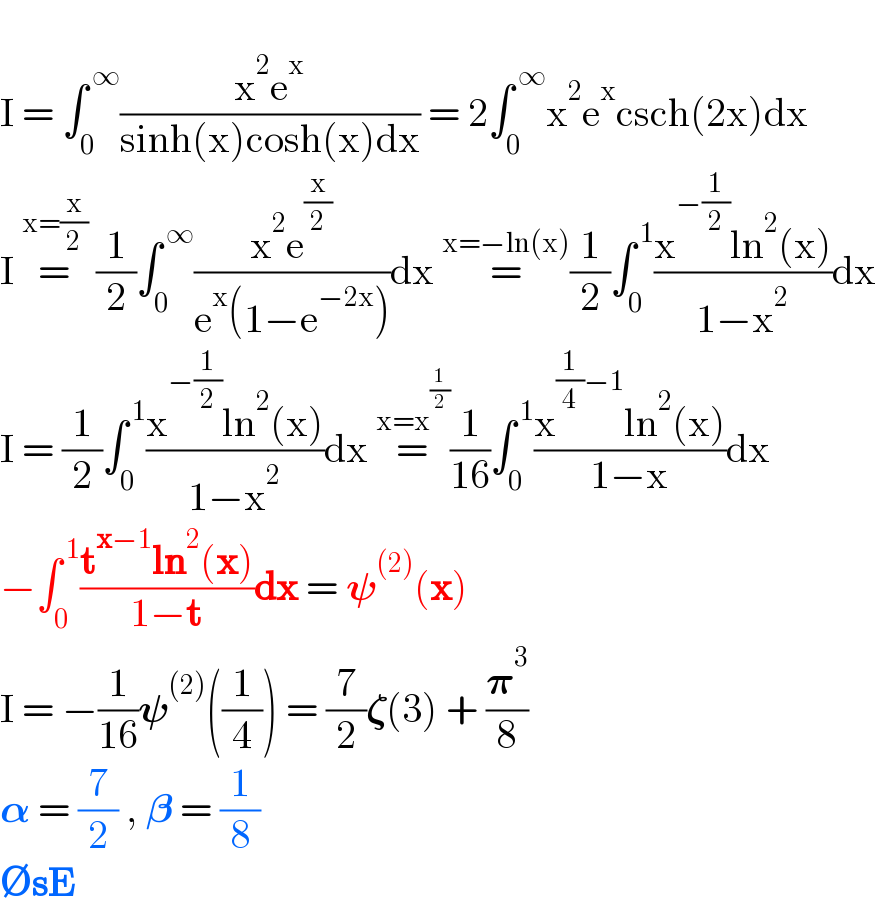
$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{x}} }{\mathrm{sinh}\left(\mathrm{x}\right)\mathrm{cosh}\left(\mathrm{x}\right)\mathrm{dx}}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\mathrm{2}} \mathrm{e}^{\mathrm{x}} \mathrm{csch}\left(\mathrm{2x}\right)\mathrm{dx} \\ $$$$\mathrm{I}\:\overset{\mathrm{x}=\frac{\mathrm{x}}{\mathrm{2}}} {=}\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{2}} \mathrm{e}^{\frac{\mathrm{x}}{\mathrm{2}}} }{\mathrm{e}^{\mathrm{x}} \left(\mathrm{1}−\mathrm{e}^{−\mathrm{2x}} \right)}\mathrm{dx}\:\overset{\mathrm{x}=−\mathrm{ln}\left(\mathrm{x}\right)} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\overset{\mathrm{x}=\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} } {=}\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{4}}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{x}}−\mathrm{1}} \boldsymbol{\mathrm{ln}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)}{\mathrm{1}−\boldsymbol{\mathrm{t}}}\boldsymbol{\mathrm{dx}}\:=\:\boldsymbol{\psi}^{\left(\mathrm{2}\right)} \left(\boldsymbol{\mathrm{x}}\right) \\ $$$$\mathrm{I}\:=\:−\frac{\mathrm{1}}{\mathrm{16}}\boldsymbol{\psi}^{\left(\mathrm{2}\right)} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)\:=\:\frac{\mathrm{7}}{\mathrm{2}}\boldsymbol{\zeta}\left(\mathrm{3}\right)\:+\:\frac{\boldsymbol{\pi}^{\mathrm{3}} }{\mathrm{8}} \\ $$$$\boldsymbol{\alpha}\:=\:\frac{\mathrm{7}}{\mathrm{2}}\:,\:\boldsymbol{\beta}\:=\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\boldsymbol{\varnothing\mathrm{sE}} \\ $$
Commented by mnjuly1970 last updated on 13/Jan/22
$${mercry}\:{sir}\:{lordos} \\ $$
Answered by mindispower last updated on 13/Jan/22

$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{4}{x}^{\mathrm{2}} {e}^{−{x}} }{\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)\left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)}{dx} \\ $$$$=\mathrm{2}\left(\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {e}^{−{x}} }{\mathrm{1}+{e}^{−\mathrm{2}{x}} }{dx}+\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{2}} {e}^{−{x}} }{\mathrm{1}−{e}^{−\mathrm{2}{x}} }\right) \\ $$$$=\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\sum}\left(\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} \left(−\mathrm{1}\right)^{{n}} {e}^{−\left(\mathrm{1}+\mathrm{2}{n}\right){x}} {dx}+\int_{\mathrm{0}} ^{\infty} {x}^{\mathrm{2}} {e}^{−\left(\mathrm{1}+\mathrm{2}{n}\right){dx}} \right. \\ $$$$=\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} }\Gamma\left(\mathrm{3}\right)+\mathrm{2}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{n}\right)^{\mathrm{3}} }\Gamma\left(\mathrm{3}\right) \\ $$$$=\mathrm{4}\beta\left(\mathrm{3}\right)+\mathrm{4}\left(\zeta\left(\mathrm{3}\right)−\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{8}}\right) \\ $$$$=\mathrm{4}\beta\left(\mathrm{3}\right)+\frac{\mathrm{7}}{\mathrm{2}}\zeta\left(\mathrm{3}\right)=\frac{\pi^{\mathrm{3}} }{\mathrm{8}}+\frac{\mathrm{7}}{\mathrm{2}}\zeta\left(\mathrm{3}\right) \\ $$$${a}+{b}=\frac{\mathrm{29}}{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 13/Jan/22
$$\:\:\:{very}\:{nice}\:{solution}\:{as}\:{always} \\ $$$${sir}\:{power}… \\ $$
Commented by mindispower last updated on 14/Jan/22
$${withe}\:{Pleasur}\:{nice}\:{day} \\ $$
Commented by mnjuly1970 last updated on 14/Jan/22

Answered by mnjuly1970 last updated on 13/Jan/22

