Question Number 163957 by HongKing last updated on 12/Jan/22
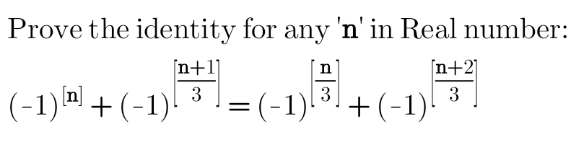
Answered by mahdipoor last updated on 12/Jan/22
![get n=3b+a , b∈N 0≤a<3 [n]=3b+[a] [((n+1)/3)]=b+[((a+1)/3)] [(n/3)]=b+[(a/3)]=b [((n+2)/3)]=b+[((a+2)/3)] ⇒(−1)^(3b+[a]) +(−1)^(b+[((a+1)/3)]) =(−1)^b +(−1)^(b+[((a+2)/3)]) ⇒(−1)^b ((−1)^([a]) +(−1)^([((a+1)/3)]) )=(−1)^b (1+(−1)^([((a+2)/3)]) ) ⇒(−1)^([a]) +(−1)^([((a+1)/3)]) =1+(−1)^([((a+2)/3)]) ⇒ { ((0≤a<1 ⇒ 1+1=1+1)),((1≤a<2 ⇒−1+1=1−1)),((2≤a<3⇒1−1=1−1 )) :}](https://www.tinkutara.com/question/Q163962.png)
$${get}\:{n}=\mathrm{3}{b}+{a}\:,\:{b}\in{N}\:\:\:\:\mathrm{0}\leqslant{a}<\mathrm{3} \\ $$$$\left[{n}\right]=\mathrm{3}{b}+\left[{a}\right]\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[\frac{{n}+\mathrm{1}}{\mathrm{3}}\right]={b}+\left[\frac{{a}+\mathrm{1}}{\mathrm{3}}\right] \\ $$$$\left[\frac{{n}}{\mathrm{3}}\right]={b}+\left[\frac{{a}}{\mathrm{3}}\right]={b}\:\:\:\:\:\:\:\:\:\:\left[\frac{{n}+\mathrm{2}}{\mathrm{3}}\right]={b}+\left[\frac{{a}+\mathrm{2}}{\mathrm{3}}\right] \\ $$$$\Rightarrow\left(−\mathrm{1}\right)^{\mathrm{3}{b}+\left[{a}\right]} +\left(−\mathrm{1}\right)^{{b}+\left[\frac{{a}+\mathrm{1}}{\mathrm{3}}\right]} =\left(−\mathrm{1}\right)^{{b}} +\left(−\mathrm{1}\right)^{{b}+\left[\frac{{a}+\mathrm{2}}{\mathrm{3}}\right]} \\ $$$$\Rightarrow\left(−\mathrm{1}\right)^{{b}} \left(\left(−\mathrm{1}\right)^{\left[{a}\right]} +\left(−\mathrm{1}\right)^{\left[\frac{{a}+\mathrm{1}}{\mathrm{3}}\right]} \right)=\left(−\mathrm{1}\right)^{{b}} \left(\mathrm{1}+\left(−\mathrm{1}\right)^{\left[\frac{{a}+\mathrm{2}}{\mathrm{3}}\right]} \right) \\ $$$$\Rightarrow\left(−\mathrm{1}\right)^{\left[{a}\right]} +\left(−\mathrm{1}\right)^{\left[\frac{{a}+\mathrm{1}}{\mathrm{3}}\right]} =\mathrm{1}+\left(−\mathrm{1}\right)^{\left[\frac{{a}+\mathrm{2}}{\mathrm{3}}\right]} \\ $$$$\Rightarrow\begin{cases}{\mathrm{0}\leqslant{a}<\mathrm{1}\:\Rightarrow\:\mathrm{1}+\mathrm{1}=\mathrm{1}+\mathrm{1}}\\{\mathrm{1}\leqslant{a}<\mathrm{2}\:\Rightarrow−\mathrm{1}+\mathrm{1}=\mathrm{1}−\mathrm{1}}\\{\mathrm{2}\leqslant{a}<\mathrm{3}\Rightarrow\mathrm{1}−\mathrm{1}=\mathrm{1}−\mathrm{1}\:}\end{cases} \\ $$
Commented by HongKing last updated on 13/Jan/22
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Sir}\:\mathrm{thank}\:\mathrm{you} \\ $$
