Question Number 164077 by mathlove last updated on 13/Jan/22
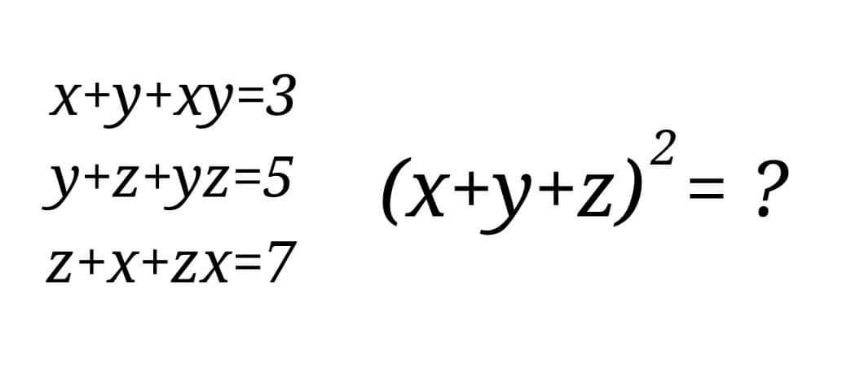
Answered by cortano1 last updated on 13/Jan/22
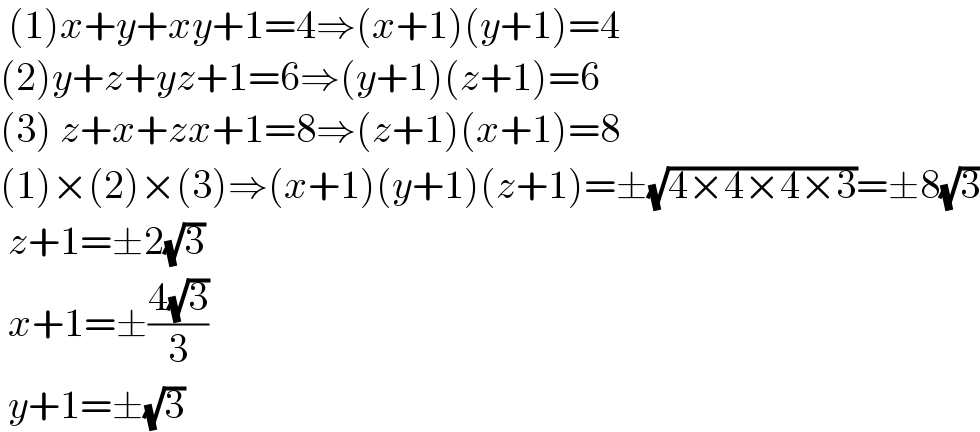
$$\:\left(\mathrm{1}\right){x}+{y}+{xy}+\mathrm{1}=\mathrm{4}\Rightarrow\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)=\mathrm{4} \\ $$$$\left(\mathrm{2}\right){y}+{z}+{yz}+\mathrm{1}=\mathrm{6}\Rightarrow\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\mathrm{6} \\ $$$$\left(\mathrm{3}\right)\:{z}+{x}+{zx}+\mathrm{1}=\mathrm{8}\Rightarrow\left({z}+\mathrm{1}\right)\left({x}+\mathrm{1}\right)=\mathrm{8} \\ $$$$\left(\mathrm{1}\right)×\left(\mathrm{2}\right)×\left(\mathrm{3}\right)\Rightarrow\left({x}+\mathrm{1}\right)\left({y}+\mathrm{1}\right)\left({z}+\mathrm{1}\right)=\pm\sqrt{\mathrm{4}×\mathrm{4}×\mathrm{4}×\mathrm{3}}=\pm\mathrm{8}\sqrt{\mathrm{3}} \\ $$$$\:{z}+\mathrm{1}=\pm\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\:{x}+\mathrm{1}=\pm\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\:{y}+\mathrm{1}=\pm\sqrt{\mathrm{3}} \\ $$
