Question Number 16409 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Jun/17
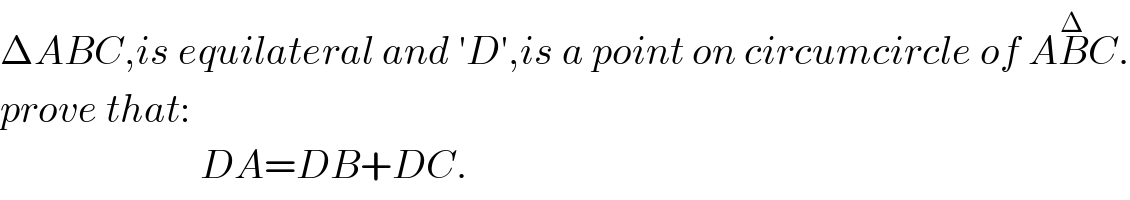
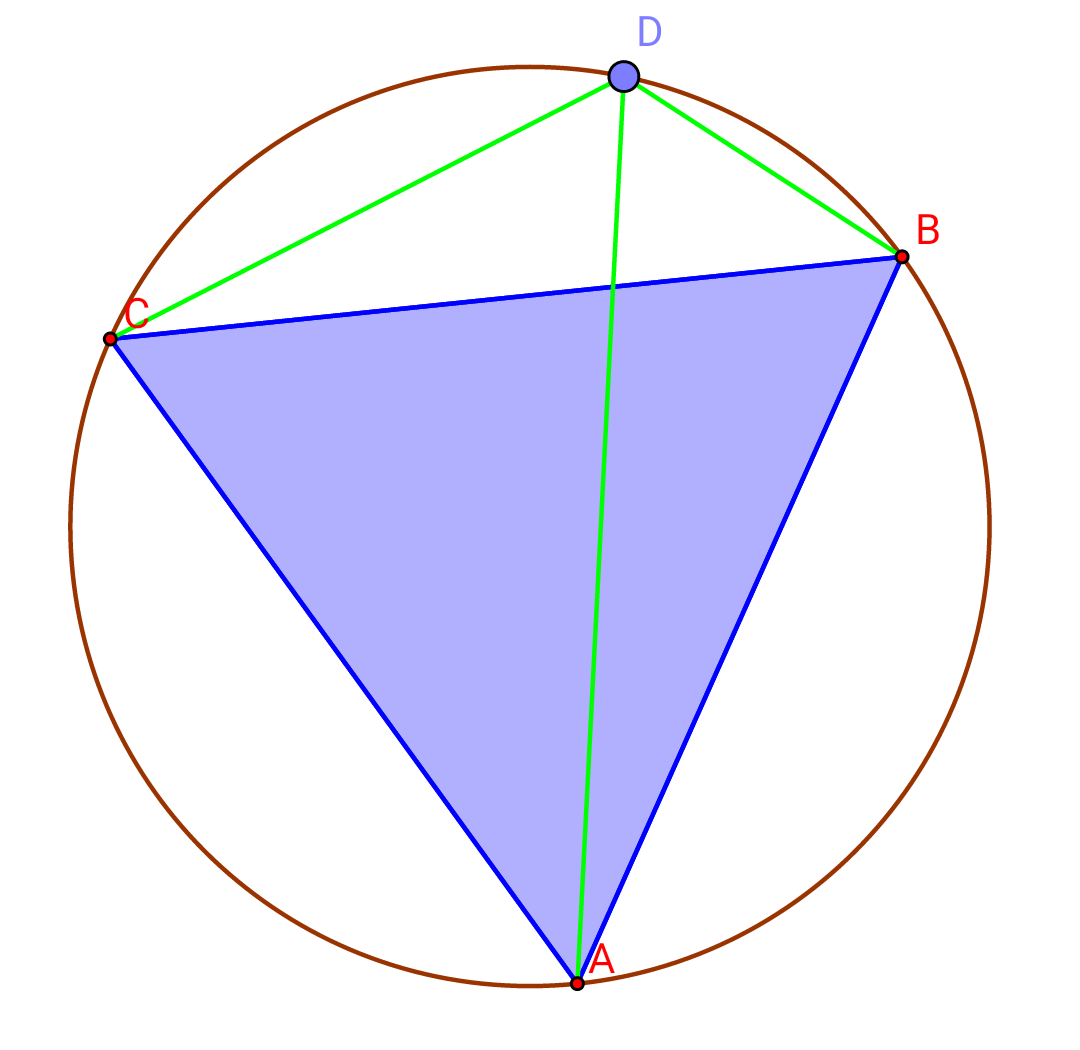
$$\Delta{ABC},{is}\:{equilateral}\:{and}\:'{D}',{is}\:{a}\:{point}\:{on}\:{circumcircle}\:{of}\:{A}\overset{\Delta} {{B}C}. \\ $$$${prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{DA}={DB}+{DC}. \\ $$
Commented by mrW1 last updated on 21/Jun/17
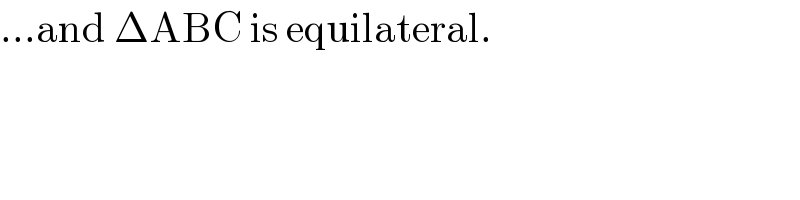
$$…\mathrm{and}\:\Delta\mathrm{ABC}\:\mathrm{is}\:\mathrm{equilateral}. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 21/Jun/17
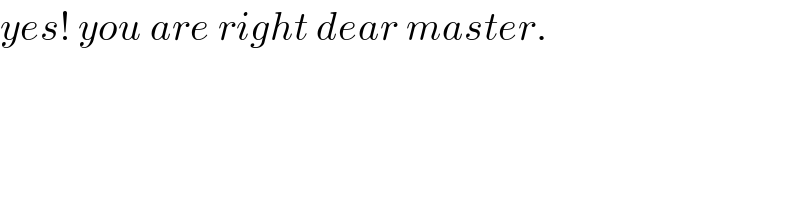
$${yes}!\:{you}\:{are}\:{right}\:{dear}\:{master}. \\ $$
Commented by RasheedSoomro last updated on 22/Jun/17

$$\mathrm{D}\:\mathrm{is}\:\boldsymbol{\mathrm{any}}\:\mathrm{point}\:\mathrm{of}\:\mathrm{cercumference} \\ $$$$\mathrm{If}\:\mathrm{D}\:\mathrm{is}\:\mathrm{beyond}\:\overset{\frown} {\mathrm{CB}}\:\:\mathrm{say}\:\mathrm{it}\:\mathrm{is}\:\mathrm{on}\:\overset{\frown} {\mathrm{AB}} \\ $$$$\mathrm{then}\:\mathrm{how}\: \\ $$$$\:\:\:\:\:\:\:\:\mathrm{DA}=\mathrm{DB}+\mathrm{DC}\:\:\:? \\ $$$$\mathrm{How}?\:\mathrm{pl}\:\mathrm{explain}. \\ $$$$ \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17
Commented by RasheedSoomro last updated on 22/Jun/17

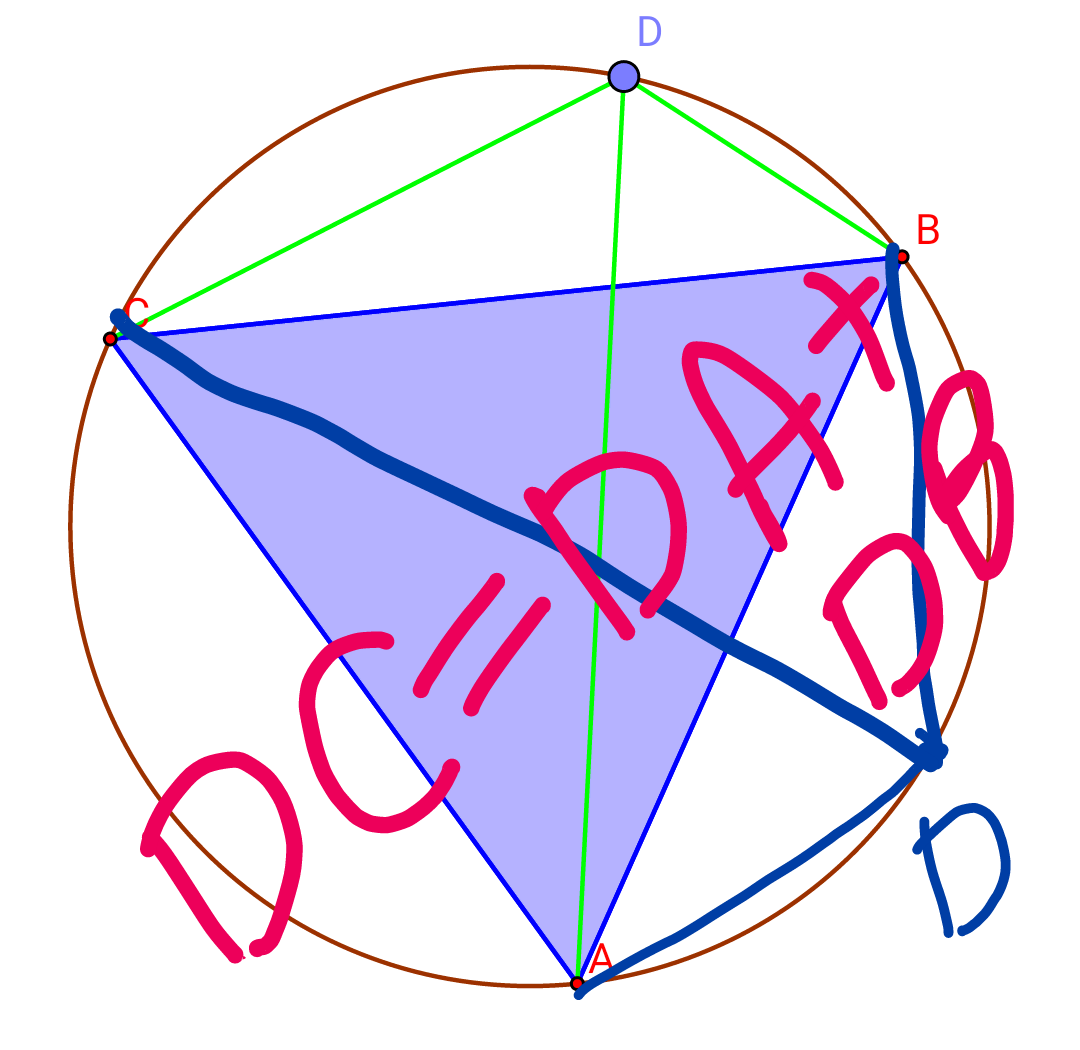
$$\mathrm{This}\:\mathrm{means}:\:\mathrm{For}\:\mathrm{the}\:\mathrm{result}\:\mathrm{DA}=\mathrm{DB}+\mathrm{DC} \\ $$$$\mathrm{D}\:\mathrm{must}\:\mathrm{be}\:\mathrm{on}\:\overset{\frown} {\mathrm{BC}}\:\:\:\:\:\mathrm{and} \\ $$$$\mathrm{for}\:\mathrm{the}\:\mathrm{result}\:\mathrm{DC}=\mathrm{DA}+\mathrm{DB}\:\:\:\mathrm{D}\:\mathrm{must}\:\mathrm{be}\:\mathrm{on} \\ $$$$\overset{\frown} {\mathrm{AB}}\:. \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{take}\:\mathrm{the}\:\mathrm{point}\:\mathrm{D}\:\mathrm{on}\:\overset{\frown} {\mathrm{AB}}\:\mathrm{the}\:\mathrm{quadrilateral} \\ $$$$\mathrm{ABDCremains}\:\mathrm{no}\:\mathrm{longer}\:\boldsymbol{\mathrm{convex}}. \\ $$$$ \\ $$
Commented by RasheedSoomro last updated on 22/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

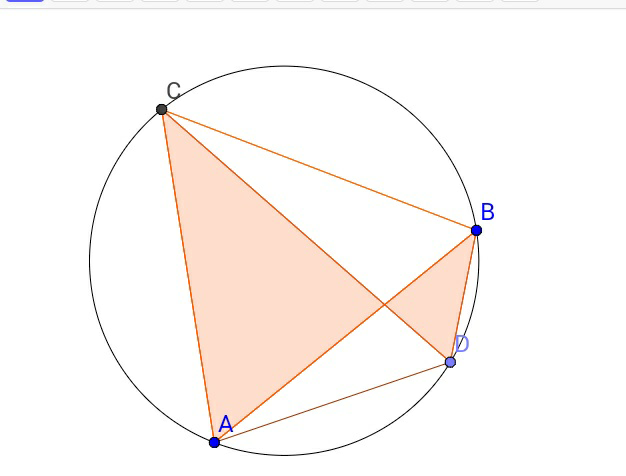
$${if}\:{we}\:{take}\:{D}\:{on}\:{AB},{relation}:{DA}={DB}+{DC} \\ $$$${is}\:{not}\:{valid}. \\ $$$${this}\:{quistion}\:{just}\:{say}\:{that}: \\ $$$${if}\:{D}\:{be}\:{a}\:{point}\:{on}\:{circumcircle},\:{and} \\ $$$${we}\:{connect}\:{this}\:{to}\:{verteses}\:{of}\:{ABC}, \\ $$$${length}\:{of}\:{longest}\:{line}\:{from}\:{D}\:{to}\:{A},{B},{or} \\ $$$${C},{equails}\:{to}\:{sum}\:{of}\:{other}\:\mathrm{2}\:\:{lines}, \\ $$$${that}\:{have}\:{smaller}\:{lengths}. \\ $$
Commented by RasheedSoomro last updated on 22/Jun/17

$$\mathrm{Now}\:\mathrm{the}\:\mathrm{statement}\:\mathrm{of}\:\mathrm{the}\:\mathrm{theorm} \\ $$$$\mathrm{is}\:\mathrm{right}\:\mathrm{sir}!\:\mathrm{Thanks}! \\ $$
Answered by Tinkutara last updated on 22/Jun/17
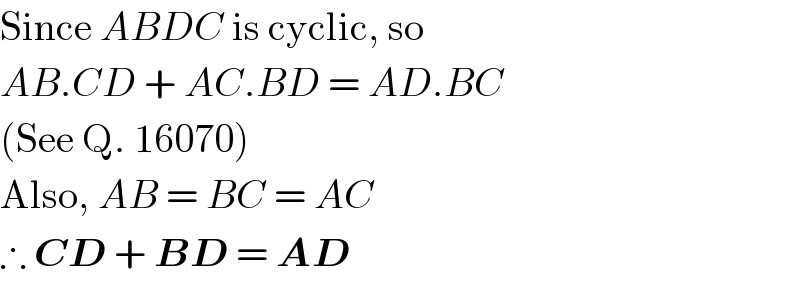
$$\mathrm{Since}\:{ABDC}\:\mathrm{is}\:\mathrm{cyclic},\:\mathrm{so} \\ $$$${AB}.{CD}\:+\:{AC}.{BD}\:=\:{AD}.{BC} \\ $$$$\left(\mathrm{See}\:\mathrm{Q}.\:\mathrm{16070}\right) \\ $$$$\mathrm{Also},\:{AB}\:=\:{BC}\:=\:{AC} \\ $$$$\therefore\:\boldsymbol{{CD}}\:+\:\boldsymbol{{BD}}\:=\:\boldsymbol{{AD}} \\ $$
Answered by ajfour last updated on 22/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17
$${thank}\:{you}\:{mr}\:{Ajfour}. \\ $$
Commented by ajfour last updated on 22/Jun/17
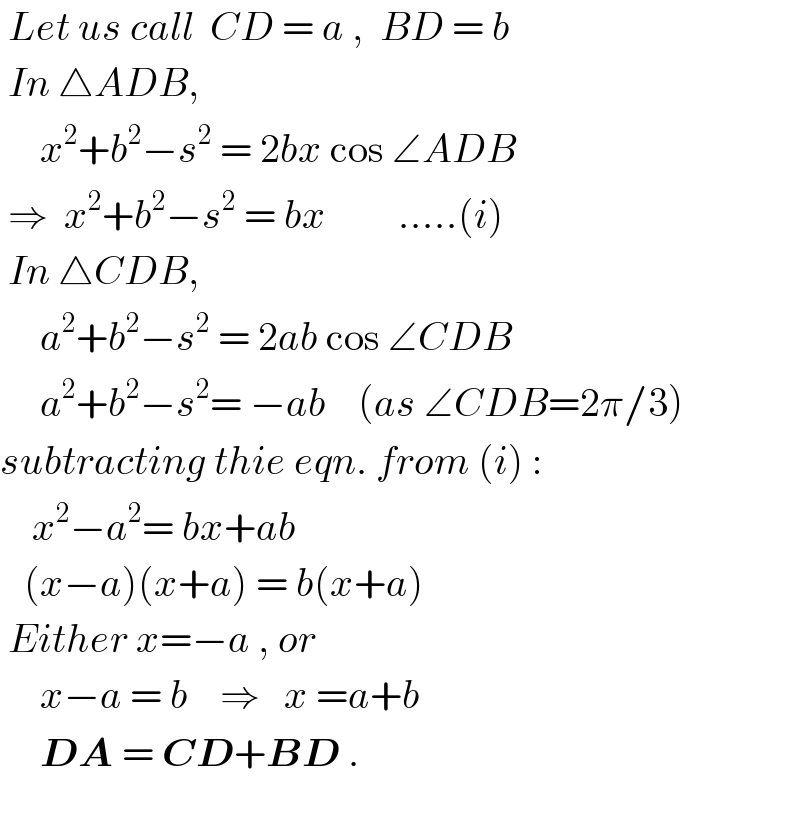
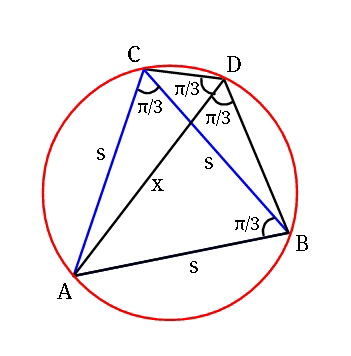
$$\:{Let}\:{us}\:{call}\:\:{CD}\:=\:{a}\:,\:\:{BD}\:=\:{b} \\ $$$$\:{In}\:\bigtriangleup{ADB}, \\ $$$$\:\:\:\:\:{x}^{\mathrm{2}} +{b}^{\mathrm{2}} −{s}^{\mathrm{2}} \:=\:\mathrm{2}{bx}\:\mathrm{cos}\:\angle{ADB}\: \\ $$$$\:\Rightarrow\:\:{x}^{\mathrm{2}} +{b}^{\mathrm{2}} −{s}^{\mathrm{2}} \:=\:{bx}\:\:\:\:\:\:\:\:\:…..\left({i}\right) \\ $$$$\:{In}\:\bigtriangleup{CDB}, \\ $$$$\:\:\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{s}^{\mathrm{2}} \:=\:\mathrm{2}{ab}\:\mathrm{cos}\:\angle{CDB} \\ $$$$\:\:\:\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{s}^{\mathrm{2}} =\:−{ab}\:\:\:\:\left({as}\:\angle{CDB}=\mathrm{2}\pi/\mathrm{3}\right) \\ $$$${subtracting}\:{thie}\:{eqn}.\:{from}\:\left({i}\right)\:: \\ $$$$\:\:\:\:{x}^{\mathrm{2}} −{a}^{\mathrm{2}} =\:{bx}+{ab} \\ $$$$\:\:\:\left({x}−{a}\right)\left({x}+{a}\right)\:=\:{b}\left({x}+{a}\right) \\ $$$$\:{Either}\:{x}=−{a}\:,\:{or}\:\: \\ $$$$\:\:\:\:\:{x}−{a}\:=\:{b}\:\:\:\:\Rightarrow\:\:\:{x}\:={a}+{b} \\ $$$$\:\:\:\:\:\boldsymbol{{DA}}\:=\:\boldsymbol{{CD}}+\boldsymbol{{BD}}\:. \\ $$$$\:\: \\ $$
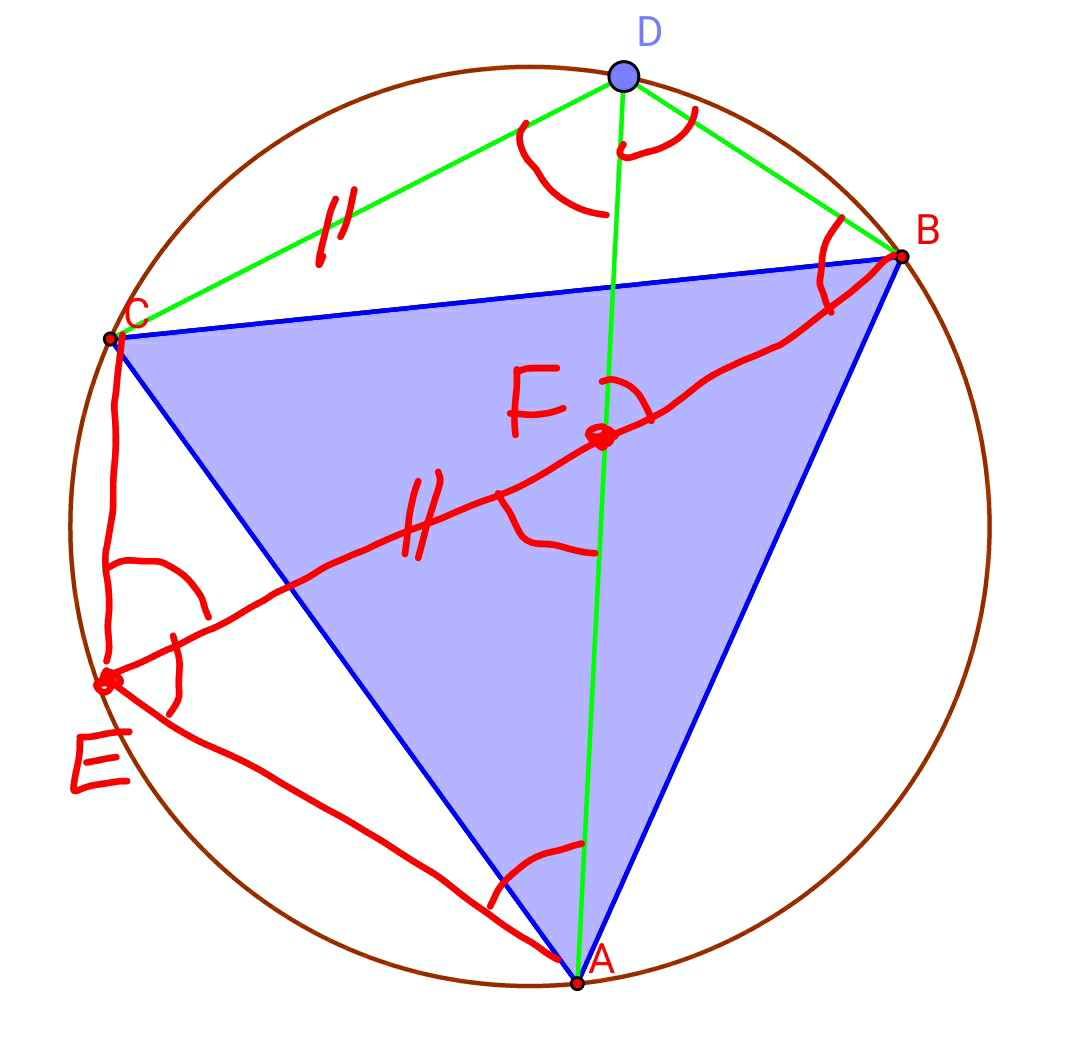
Answered by mrW1 last updated on 22/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17
$${thank}\:{you}\:{mrW}\mathrm{1}. \\ $$
Commented by mrW1 last updated on 22/Jun/17

$$\mathrm{add}\:\mathrm{EB}\://\:\mathrm{CD} \\ $$$$\angle\mathrm{CDA}=\angle\mathrm{CEB}=\mathrm{60}° \\ $$$$… \\ $$$$\mathrm{CDFE}\:\mathrm{is}\:\mathrm{parallelogram}, \\ $$$$\Rightarrow\mathrm{CD}=\mathrm{CF} \\ $$$$\Delta\mathrm{DBF}\:\mathrm{and}\:\Delta\mathrm{AFE}\:\mathrm{are}\:\mathrm{equilateral}, \\ $$$$\Rightarrow\mathrm{DB}=\mathrm{DF} \\ $$$$\Rightarrow\mathrm{CD}=\mathrm{EF}=\mathrm{FA} \\ $$$$\Rightarrow\mathrm{DB}+\mathrm{CD}=\mathrm{DF}+\mathrm{FA}=\mathrm{DA} \\ $$
