Question Number 164176 by mathlove last updated on 15/Jan/22
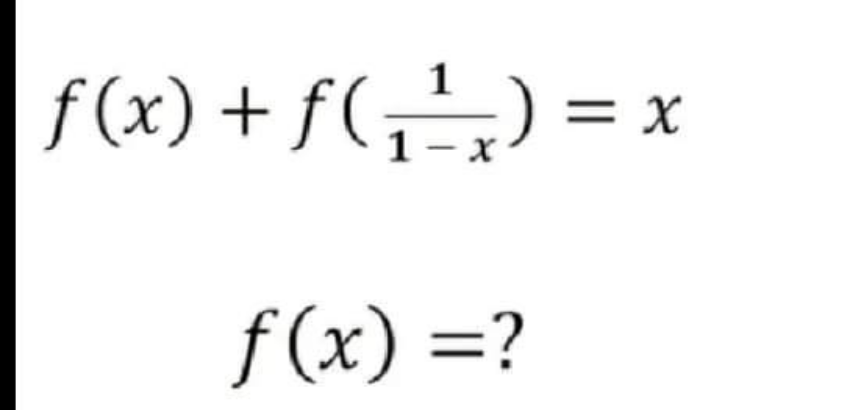
Answered by mr W last updated on 15/Jan/22

$${f}\left({x}\right)+{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)={x}\:\:\:\:…\left({i}\right) \\ $$$${replace}\:{x}\:{with}\:\mathrm{1}−\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)+{f}\left({x}\right)=\mathrm{1}−\frac{\mathrm{1}}{{x}}\:\:\:…\left({ii}\right) \\ $$$${replace}\:{x}\:{with}\:\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow\:{f}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right)+{f}\left(\frac{{x}−\mathrm{1}}{{x}}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$$\left({i}\right)+\left({ii}\right)−\left({iii}\right): \\ $$$$\mathrm{2}{f}\left({x}\right)={x}+\mathrm{1}−\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\Rightarrow{f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\mathrm{1}−\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\mathrm{1}−{x}}\right) \\ $$
Commented by Tawa11 last updated on 16/Jan/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by qaz last updated on 15/Jan/22

$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{x}−\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right) \\ $$$$=\mathrm{x}−\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}−\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}}\right)\right) \\ $$$$=\mathrm{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}+\mathrm{f}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right) \\ $$$$=\mathrm{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}+\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}\right)}\right)\right) \\ $$$$=\mathrm{x}−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{f}\left(\mathrm{x}\right) \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}−\frac{\mathrm{1}}{\mathrm{2}−\mathrm{2x}}−\frac{\mathrm{1}}{\mathrm{2x}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$
