Menu Close

Question-164193

Tinku Tara 0 Comments
Pin




Question Number 164193 by mathlove last updated on 15/Jan/22
Commented by MJS_new last updated on 15/Jan/22
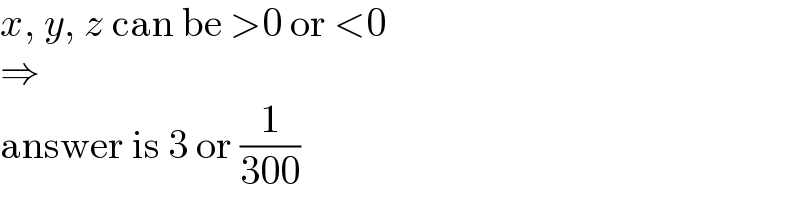
x, y, z can be >0 or <0 ⇒ answer is 3 or (1/(300))
$${x},\:{y},\:{z}\:\mathrm{can}\:\mathrm{be}\:>\mathrm{0}\:\mathrm{or}\:<\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{3}\:\mathrm{or}\:\frac{\mathrm{1}}{\mathrm{300}} \\ $$
Commented by cortano1 last updated on 16/Jan/22
how to get (1/(300))?
$${how}\:{to}\:{get}\:\frac{\mathrm{1}}{\mathrm{300}}? \\ $$
Answered by cortano1 last updated on 15/Jan/22
2^x = k⇒x=log _2 k 3^y =k⇒y=log _3 k 5^z =k⇒z=log _5 k 30^((1/x)+(1/y)+(1/z)) = 30^(log _k (2×3×5)) = k 30^(log _k (30)) = k ⇒log _k (30)=log _(30) (k) k=30⇒ ((30×3)/(30)) = 3
$$\:\mathrm{2}^{{x}} =\:{k}\Rightarrow{x}=\mathrm{log}\:_{\mathrm{2}} {k} \\ $$$$\:\mathrm{3}^{{y}} ={k}\Rightarrow{y}=\mathrm{log}\:_{\mathrm{3}} {k} \\ $$$$\:\mathrm{5}^{{z}} ={k}\Rightarrow{z}=\mathrm{log}\:_{\mathrm{5}} {k} \\ $$$$\:\mathrm{30}^{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}} =\:\mathrm{30}^{\mathrm{log}\:_{{k}} \left(\mathrm{2}×\mathrm{3}×\mathrm{5}\right)} \:=\:{k} \\ $$$$\:\mathrm{30}^{\mathrm{log}\:_{{k}} \left(\mathrm{30}\right)} =\:{k}\:\Rightarrow\mathrm{log}\:_{{k}} \left(\mathrm{30}\right)=\mathrm{log}\:_{\mathrm{30}} \left({k}\right) \\ $$$$\:{k}=\mathrm{30}\Rightarrow\:\frac{\mathrm{30}×\mathrm{3}}{\mathrm{30}}\:=\:\mathrm{3} \\ $$
Answered by mr W last updated on 16/Jan/22
2^x =3^y =5^z =30^((1/x)+(1/y)+(1/z)) =k x=((log k)/(log 2)) y=((log k)/(log 3)) z=((log k)/(log 5)) (1/x)+(1/y)+(1/z)=((log k)/(log 30)) ((log 2+log 3+log 5)/(log k))=((log k)/(log 30)) ((log 30)/(log k))=((log k)/(log 30)) (log k)^2 =(log 30)^2 ⇒log k=±log 30 ⇒k=30^(±1) ,i.e. 30 or (1/(30)) ((2^x +3^y +5^z )/(30))=((3k)/(30))=(k/(10))= { ((((30)/(10))=3)),(((1/(30×10))=(1/(300)))) :}
$$\mathrm{2}^{{x}} =\mathrm{3}^{{y}} =\mathrm{5}^{{z}} =\mathrm{30}^{\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}} ={k} \\ $$$${x}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{2}} \\ $$$${y}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{3}} \\ $$$${z}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{5}} \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{30}} \\ $$$$\frac{\mathrm{log}\:\mathrm{2}+\mathrm{log}\:\mathrm{3}+\mathrm{log}\:\mathrm{5}}{\mathrm{log}\:{k}}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{30}} \\ $$$$\frac{\mathrm{log}\:\mathrm{30}}{\mathrm{log}\:{k}}=\frac{\mathrm{log}\:{k}}{\mathrm{log}\:\mathrm{30}} \\ $$$$\left(\mathrm{log}\:{k}\right)^{\mathrm{2}} =\left(\mathrm{log}\:\mathrm{30}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{log}\:{k}=\pm\mathrm{log}\:\mathrm{30} \\ $$$$\Rightarrow{k}=\mathrm{30}^{\pm\mathrm{1}} ,{i}.{e}.\:\mathrm{30}\:{or}\:\frac{\mathrm{1}}{\mathrm{30}} \\ $$$$\frac{\mathrm{2}^{{x}} +\mathrm{3}^{{y}} +\mathrm{5}^{{z}} }{\mathrm{30}}=\frac{\mathrm{3}{k}}{\mathrm{30}}=\frac{{k}}{\mathrm{10}}=\begin{cases}{\frac{\mathrm{30}}{\mathrm{10}}=\mathrm{3}}\\{\frac{\mathrm{1}}{\mathrm{30}×\mathrm{10}}=\frac{\mathrm{1}}{\mathrm{300}}}\end{cases} \\ $$
Commented by Tawa11 last updated on 16/Jan/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *