Menu Close

Question-164305

Tinku Tara 0 Comments
Pin




Question Number 164305 by ajfour last updated on 16/Jan/22
Commented by ajfour last updated on 16/Jan/22
Find (r/R) , if all colored regions (blue, brown, maroon) have equal areas. Take h=7.
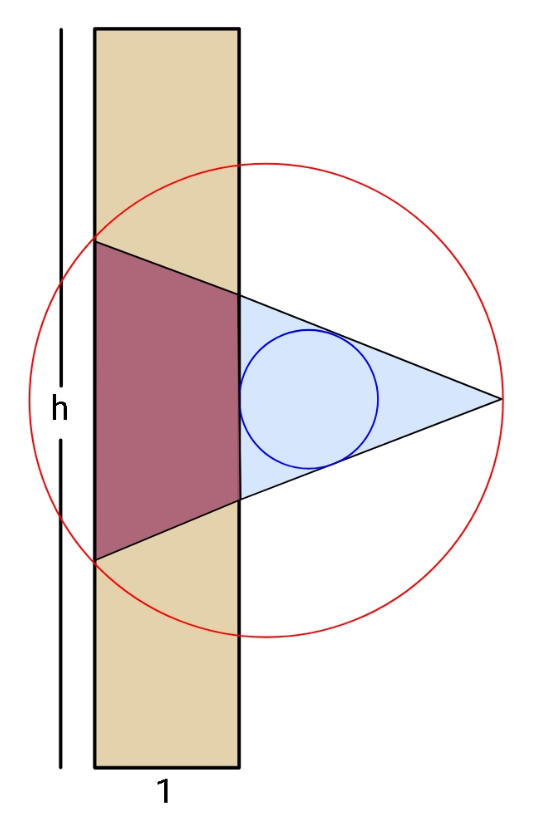
$${Find}\:\:\frac{{r}}{{R}}\:,\:\:{if}\:{all}\:{colored}\:{regions} \\ $$$$\:\:\:\:\:\left({blue},\:{brown},\:{maroon}\right)\:{have} \\ $$$$\:\:{equal}\:{areas}.\:\:\:{Take}\:{h}=\mathrm{7}. \\ $$
Answered by mr W last updated on 16/Jan/22
Commented by mr W last updated on 16/Jan/22
area of each region is ((h×1)/3)=(h/3) (((R+(√(R^2 −(b^2 /4)))−1)/(R+(√(R^2 −(b^2 /4))))))^2 =(1/2) ((R+(√(R^2 −(b^2 /4)))−1)/(R+(√(R^2 −(b^2 /4)))))=(1/( (√2))) (1/(R+(√(R^2 −(b^2 /4)))))=1−(1/( (√2)))=(((√2)−1)/( (√2))) R+(√(R^2 −(b^2 /4)))=((√2)/( (√2)−1))=2+(√2) (√(R^2 −(b^2 /4)))=2+(√2)−R R^2 −(b^2 /4)=(2+(√2))^2 +R^2 −2(2+(√2))R (2+(√2))^2 +(b^2 /4)=2(2+(√2))R ⇒R=1+((√2)/2)+(((2−(√2))b^2 )/(16)) ...(i) (b/2)×(R+(√(R^2 −(b^2 /4))))=2×(h/3) ⇒b(R+(√(R^2 −(b^2 /4))))=((4h)/3) ...(ii) ((R+(√(R^2 −(b^2 /4)))−1−r)/r)=((2(√([R+(√(R^2 −(b^2 /4)))]^2 +(b^2 /4))))/b) ((R+(√(R^2 −(b^2 /4)))−1)/r)=1+((2(√(2R(R+(√(R^2 −(b^2 /4)))))))/( b)) ⇒r=((R+(√(R^2 −(b^2 /4)))−1)/(1+((2(√(2R(R+(√(R^2 −(b^2 /4)))))))/b))) ...(iii) example: h=7 ⇒b≈2.7337 ⇒R≈1.9807 ⇒r≈0.6542
$${area}\:{of}\:{each}\:{region}\:{is}\:\frac{{h}×\mathrm{1}}{\mathrm{3}}=\frac{{h}}{\mathrm{3}} \\ $$$$\left(\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\frac{\mathrm{1}}{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}=\mathrm{2}+\sqrt{\mathrm{2}}−{R} \\ $$$${R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){R} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{2}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right){R} \\ $$$$\Rightarrow{R}=\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right){b}^{\mathrm{2}} }{\mathrm{16}}\:\:\:…\left({i}\right) \\ $$$$\frac{{b}}{\mathrm{2}}×\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)=\mathrm{2}×\frac{{h}}{\mathrm{3}} \\ $$$$\Rightarrow{b}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)=\frac{\mathrm{4}{h}}{\mathrm{3}}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}−{r}}{{r}}=\frac{\mathrm{2}\sqrt{\left[{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right]^{\mathrm{2}} +\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}}{{b}} \\ $$$$\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{{r}}=\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{2}{R}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)}}{\:{b}} \\ $$$$\Rightarrow{r}=\frac{{R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}−\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}\sqrt{\mathrm{2}{R}\left({R}+\sqrt{{R}^{\mathrm{2}} −\frac{{b}^{\mathrm{2}} }{\mathrm{4}}}\right)}}{{b}}}\:\:\:…\left({iii}\right) \\ $$$$ \\ $$$${example}:\:{h}=\mathrm{7} \\ $$$$\Rightarrow{b}\approx\mathrm{2}.\mathrm{7337} \\ $$$$\Rightarrow{R}\approx\mathrm{1}.\mathrm{9807} \\ $$$$\Rightarrow{r}\approx\mathrm{0}.\mathrm{6542} \\ $$
Commented by mr W last updated on 16/Jan/22
Commented by mr W last updated on 16/Jan/22
check: b=2.7337 R=1.9807 (√(R^2 −((b/2))^2 ))=1.4335 area of big triangle =((2.7337×(1.9807+1.4335))/2)=4.6667 =(7/3)×2 ✓ area of small triangle =4.6667×(((1.9807+1.4335−1)/(1.9807+1.4335)))^2 =2.3333 =(7/3) ✓
$${check}: \\ $$$${b}=\mathrm{2}.\mathrm{7337} \\ $$$${R}=\mathrm{1}.\mathrm{9807} \\ $$$$\sqrt{{R}^{\mathrm{2}} −\left(\frac{{b}}{\mathrm{2}}\right)^{\mathrm{2}} }=\mathrm{1}.\mathrm{4335} \\ $$$${area}\:{of}\:{big}\:{triangle} \\ $$$$=\frac{\mathrm{2}.\mathrm{7337}×\left(\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}\right)}{\mathrm{2}}=\mathrm{4}.\mathrm{6667} \\ $$$$=\frac{\mathrm{7}}{\mathrm{3}}×\mathrm{2}\:\checkmark \\ $$$${area}\:{of}\:{small}\:{triangle} \\ $$$$=\mathrm{4}.\mathrm{6667}×\left(\frac{\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}−\mathrm{1}}{\mathrm{1}.\mathrm{9807}+\mathrm{1}.\mathrm{4335}}\right)^{\mathrm{2}} =\mathrm{2}.\mathrm{3333} \\ $$$$=\frac{\mathrm{7}}{\mathrm{3}}\:\checkmark \\ $$
Commented by ajfour last updated on 16/Jan/22
Yeah, i also got it sir.
$${Yeah},\:{i}\:{also}\:{got}\:{it}\:{sir}. \\ $$
Commented by Tawa11 last updated on 16/Jan/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Answered by ajfour last updated on 16/Jan/22
Commented by ajfour last updated on 16/Jan/22
area=a=(h/3)=pq y_B =b=(q/p)(p+1) a_(maroon) =b+q=pq ⇒ p+1=p(p−1) p^2 −2p−1=0 p=1+(√2) q=((h((√2)−1))/3) tan θ=(q/p)=(h/3)((((√2)−1)/( (√2)+1)))=λ sin θ=(r/(p−r)) ⇒ r=((psin θ)/(1+sin θ)) r=((((√2)+1)λ)/(λ+(√(λ^2 +1)))) tan 2θ=(b/(p+1−R)) ⇒ R=p+1−(b/(tan 2θ)) R=2+(√2)−(((1−λ^2 )(2+(√2)))/2) =(1+(1/( (√2))))(1+λ^2 ) example h=7 2b≈2.73 r≈0.654 R≈1.98
$${area}={a}=\frac{{h}}{\mathrm{3}}={pq} \\ $$$${y}_{{B}} ={b}=\frac{{q}}{{p}}\left({p}+\mathrm{1}\right) \\ $$$${a}_{{maroon}} ={b}+{q}={pq}\:\:\:\: \\ $$$$\Rightarrow\:\:\:\:\:{p}+\mathrm{1}={p}\left({p}−\mathrm{1}\right) \\ $$$${p}^{\mathrm{2}} −\mathrm{2}{p}−\mathrm{1}=\mathrm{0} \\ $$$${p}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$${q}=\frac{{h}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\theta=\frac{{q}}{{p}}=\frac{{h}}{\mathrm{3}}\left(\frac{\sqrt{\mathrm{2}}−\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}\right)=\lambda \\ $$$$\mathrm{sin}\:\theta=\frac{{r}}{{p}−{r}}\:\:\Rightarrow\:\:{r}=\frac{{p}\mathrm{sin}\:\theta}{\mathrm{1}+\mathrm{sin}\:\theta} \\ $$$$\:\:\:{r}=\frac{\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\lambda}{\lambda+\sqrt{\lambda^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{tan}\:\mathrm{2}\theta=\frac{{b}}{{p}+\mathrm{1}−{R}} \\ $$$$\Rightarrow \\ $$$${R}={p}+\mathrm{1}−\frac{{b}}{\mathrm{tan}\:\mathrm{2}\theta} \\ $$$$\:\:\:{R}=\mathrm{2}+\sqrt{\mathrm{2}}−\frac{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\left(\mathrm{1}+\lambda^{\mathrm{2}} \right) \\ $$$${example}\:\:\:{h}=\mathrm{7} \\ $$$$\:\:\:\mathrm{2}{b}\approx\mathrm{2}.\mathrm{73} \\ $$$$\:\:{r}\approx\mathrm{0}.\mathrm{654} \\ $$$$\:\:{R}\approx\mathrm{1}.\mathrm{98} \\ $$
Commented by mr W last updated on 16/Jan/22
perfect! better than my solution which delivers only approximated result.
$${perfect}!\:{better}\:{than}\:{my}\:{solution}\:{which} \\ $$$${delivers}\:{only}\:{approximated}\:{result}. \\ $$
Commented by Tawa11 last updated on 16/Jan/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *