Menu Close

Question-164395

Tinku Tara 0 Comments
Pin




Question Number 164395 by amin96 last updated on 16/Jan/22
Answered by mnjuly1970 last updated on 17/Jan/22
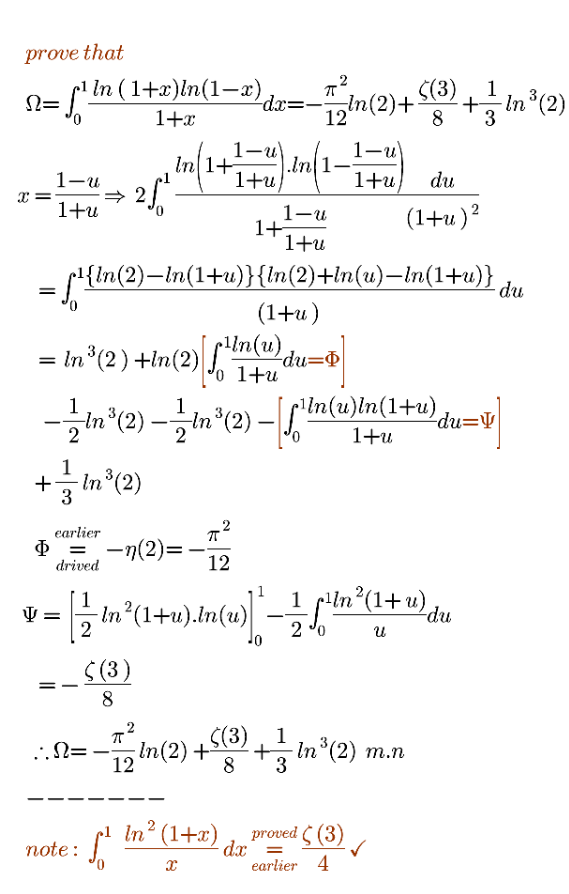
Commented by mnjuly1970 last updated on 17/Jan/22
thank you so much my dear friend sir amin ....yashasin azerbaijan
$$\:\:{thank}\:{you}\:{so}\:{much}\:{my}\:{dear}\:{friend} \\ $$$${sir}\:{amin}\:….{yashasin}\:{azerbaijan} \\ $$
Commented by amin96 last updated on 17/Jan/22
Bravo my dear sir thank you
$$\boldsymbol{\mathrm{Bravo}}\:\boldsymbol{\mathrm{my}}\:\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{thank}}\:\boldsymbol{\mathrm{you}}\: \\ $$
Answered by Lordose last updated on 17/Jan/22
Ω = ∫_0 ^( 1) ((ln(1+x)ln(1−x))/(1+x))dx Ω = −(1/2)(∫_0 ^( 1) ln^2 (((1−x)/(1+x)))(dx/(1+x)) − ∫_0 ^( 1) ((ln^2 (1−x))/(1+x))dx −∫_0 ^( 1) ((ln^2 (1+x))/(1+x))dx) Ω = −(1/2)(A − B − C) A =^(x=((1−x)/(1+x))) 2∫_0 ^( 1) ((ln^2 (x))/(1+x)) = 2Σ_(n=1) ^∞ (−1)^(n−1) ∫_0 ^( 1) x^(n−1) ln^2 (x)dx A =^(IBP×2) 2Σ_(n=1) ^∞ (((−1)^(n−1) )/n^3 ) = 2𝛈(3) B =^(x=1−x) ∫_0 ^( 1) ((ln^2 (x))/(2(1−(x/2))))dx = Σ_(n=1) ^∞ ((1/2))^n ∫_0 ^( 1) x^(n−1) ln^2 (x)dx B = Σ_(n=1) ^∞ ((1/2))^n ∙(1/n^3 ) = 2Li_3 ((1/2)) C =^(x=1+x) ∫_1 ^( 2) ((ln^2 (x))/x)dx =^(x=ln(x)) ∫_0 ^( ln(2)) x^2 dx = ((ln^3 (2))/3) Ω = −(1/2)(2𝛈(3) − 2Li_3 ((1/2)) − ((ln^3 (2))/3)) Ω = −(3/8)𝛇(3) + (((ln^3 (2))/6) − ((𝛑^2 ln(2))/(12)) + (7/8)𝛇(3)) + ((ln^3 (2))/6) 𝛀 = ((ln^3 (2))/3) − ((𝛑^2 ln(2))/(12)) + ((𝛇(3))/8) ∅sE
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}}\:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx}\right) \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\:−\:\mathrm{B}\:−\:\mathrm{C}\right) \\ $$$$\mathrm{A}\:\overset{\mathrm{x}=\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}} {=}\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\:=\:\mathrm{2}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{A}\:\overset{\boldsymbol{\mathrm{IBP}}×\mathrm{2}} {=}\mathrm{2}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{3}} }\:=\:\mathrm{2}\boldsymbol{\eta}\left(\mathrm{3}\right) \\ $$$$\mathrm{B}\:\overset{\mathrm{x}=\mathrm{1}−\mathrm{x}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{x}}{\mathrm{2}}\right)}\mathrm{dx}\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{B}\:=\:\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}} \centerdot\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:=\:\mathrm{2}\boldsymbol{\mathrm{Li}}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\mathrm{C}\:\overset{\mathrm{x}=\mathrm{1}+\mathrm{x}} {=}\int_{\mathrm{1}} ^{\:\mathrm{2}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\overset{\mathrm{x}=\mathrm{ln}\left(\mathrm{x}\right)} {=}\int_{\mathrm{0}} ^{\:\mathrm{ln}\left(\mathrm{2}\right)} \mathrm{x}^{\mathrm{2}} \mathrm{dx}\:=\:\frac{\mathrm{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}} \\ $$$$\Omega\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2}\boldsymbol{\eta}\left(\mathrm{3}\right)\:−\:\mathrm{2}\boldsymbol{\mathrm{Li}}_{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:−\:\frac{\mathrm{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}\right) \\ $$$$\Omega\:=\:−\frac{\mathrm{3}}{\mathrm{8}}\boldsymbol{\zeta}\left(\mathrm{3}\right)\:+\:\left(\frac{\mathrm{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}}\:−\:\frac{\boldsymbol{\pi}^{\mathrm{2}} \mathrm{ln}\left(\mathrm{2}\right)}{\mathrm{12}}\:+\:\frac{\mathrm{7}}{\mathrm{8}}\boldsymbol{\zeta}\left(\mathrm{3}\right)\right)\:+\:\frac{\mathrm{ln}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{6}} \\ $$$$\boldsymbol{\Omega}\:=\:\frac{\boldsymbol{\mathrm{ln}}^{\mathrm{3}} \left(\mathrm{2}\right)}{\mathrm{3}}\:−\:\frac{\boldsymbol{\pi}^{\mathrm{2}} \boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)}{\mathrm{12}}\:+\:\frac{\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$\boldsymbol{\varnothing\mathrm{sE}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *