Question Number 16441 by mrW1 last updated on 22/Jun/17

Commented by mrW1 last updated on 22/Jun/17

$$\mathrm{What}\:\mathrm{was}\:\mathrm{the}\:\mathrm{question}\:\mathrm{to}\:\mathrm{this}\:\mathrm{diagram}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17
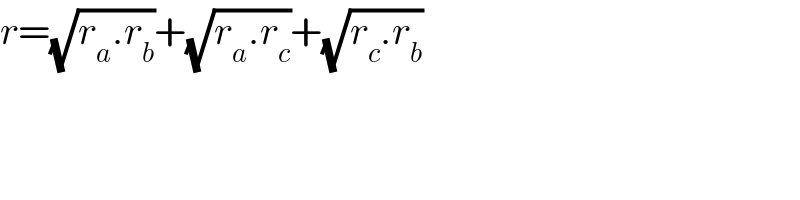
$${r}=\sqrt{{r}_{{a}} .{r}_{{b}} }+\sqrt{{r}_{{a}} .{r}_{{c}} }+\sqrt{{r}_{{c}} .{r}_{{b}} } \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 23/Jun/17
![cos(A/2)=((2(√(r.r_a )))/(r+r_a ))=m m=((2(√(r.r_a )))/(r+r_a ))⇒m^2 =((4r.r_a )/((r+r_a )^2 )) ⇒m^2 (r+r_a )^2 −4r.r_a =0 ⇒r_a ^2 +2r(1−(2/m^2 ))r_a +r^2 =0 ⇒r_a =((−2r(1−(2/m^2 ))+(√(4r^2 (1−(2/m^2 ))^2 −4r^2 )))/2)= r_a =r(((2(√(1−m^2 )))/m^2 )−1+(2/m^2 ))=r.((2(√(1−m^2 ))−m^2 +2)/m^2 )= =r.((1−m^2 +2(√(1−m^2 ))+1)/m^2 )=r.((((√(1−m^2 ))+1)^2 )/m^2 ) 1−m^2 =1−cos^2 (A/2)=sin^2 (A/2) ⇒r_a =r.(((1+sin(A/2))^2 )/(cos^2 (A/2)))=r.(((1+sin(A/2))/(cos(A/2))))^2 r_b =r.(((1+sin(B/2))/(cos(B/2))))^2 ,r_c =r.(((1+sin(C/2))/(cos(C/2))))^2 ⇒(√(r_a .r_b ))+(√(r_b .r_c ))+(√(r_c .r_a ))= =r.[(((1+sin(A/2))(1+sin(B/2)))/(cos(A/2).cos(B/2)))+(((1+sin(B/2))(1+sin(C/2)))/(cos(B/2).cos(C/2)))+ +(((1+sin(A/2))(1+sin(C/2)))/(cos(A/2).cos(C/2)))]= =r.[((cos(C/2)+cos(C/2)sin(A/2)+cos(C/2)sin(B/2)+cos(C/2)sin(A/2)sin(B/2))/(cos(A/2)cos(B/2)cos(C/2)))+ +((cos(A/2)+cos(A/2)sin(B/2)+cos(A/2)sin(C/2)+cos(A/2)sin(B/2)sin(C/2))/(cos(A/2)cos(B/2)cos(C/2)))+ +((cos(B/2)+cos(B/2)sin(A/2)+cos(B/2)sin(C/2)+cos(B/2)sin(A/2)sin(C/2))/(cos(A/2)cos(B/2)cos(C/2)))]= =r.[((Σcos(A/2)+Σsin((A+B)/2)+Σcos(A/2)sin(B/2)sin(C/2))/(Πcos(A/2)))]= =r.[((2Σcos(A/2)+Σcos(A/2)sin(B/2)sin(C/2))/(Πcos(A/2)))]= Σcos(A/2)sin(B/2)sin(C/2)=Σ(√((p(p−a))/(bc)))(√(((p−a)(p−c)(p−a)(p−b))/(ac.ab)))= =Σ(((p−a).S)/(abc))=(((3p−a−b−c).S)/(abc))=((p.S)/(4R.S))=(p/(4R)) Πcos(A/2)=Π(√((p(p−a))/(bc)))=((p.S)/(abc))=((p.S)/(4R.S))=(p/(4R)) ⇒Σ(√(r_a .r_b ))=r.(1+((8RΣcos(A/2))/p)) i think there is some thing wrong. please someone recheck my solution.](https://www.tinkutara.com/question/Q16480.png)
$${cos}\frac{{A}}{\mathrm{2}}=\frac{\mathrm{2}\sqrt{{r}.{r}_{{a}} }}{{r}+{r}_{{a}} }={m} \\ $$$${m}=\frac{\mathrm{2}\sqrt{{r}.{r}_{{a}} }}{{r}+{r}_{{a}} }\Rightarrow{m}^{\mathrm{2}} =\frac{\mathrm{4}{r}.{r}_{{a}} }{\left({r}+{r}_{{a}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow{m}^{\mathrm{2}} \left({r}+{r}_{{a}} \right)^{\mathrm{2}} −\mathrm{4}{r}.{r}_{{a}} =\mathrm{0} \\ $$$$\Rightarrow{r}_{{a}} ^{\mathrm{2}} +\mathrm{2}{r}\left(\mathrm{1}−\frac{\mathrm{2}}{{m}^{\mathrm{2}} }\right){r}_{{a}} +{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{r}_{{a}} =\frac{−\mathrm{2}{r}\left(\mathrm{1}−\frac{\mathrm{2}}{{m}^{\mathrm{2}} }\right)+\sqrt{\mathrm{4}{r}^{\mathrm{2}} \left(\mathrm{1}−\frac{\mathrm{2}}{{m}^{\mathrm{2}} }\right)^{\mathrm{2}} −\mathrm{4}{r}^{\mathrm{2}} }}{\mathrm{2}}= \\ $$$${r}_{{a}} ={r}\left(\frac{\mathrm{2}\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }}{{m}^{\mathrm{2}} }−\mathrm{1}+\frac{\mathrm{2}}{{m}^{\mathrm{2}} }\right)={r}.\frac{\mathrm{2}\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }−{m}^{\mathrm{2}} +\mathrm{2}}{{m}^{\mathrm{2}} }= \\ $$$$={r}.\frac{\mathrm{1}−{m}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }+\mathrm{1}}{{m}^{\mathrm{2}} }={r}.\frac{\left(\sqrt{\mathrm{1}−{m}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }{{m}^{\mathrm{2}} } \\ $$$$\mathrm{1}−{m}^{\mathrm{2}} =\mathrm{1}−{cos}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}={sin}^{\mathrm{2}} \frac{{A}}{\mathrm{2}} \\ $$$$\Rightarrow{r}_{{a}} ={r}.\frac{\left(\mathrm{1}+{sin}\frac{{A}}{\mathrm{2}}\right)^{\mathrm{2}} }{{cos}^{\mathrm{2}} \frac{{A}}{\mathrm{2}}}={r}.\left(\frac{\mathrm{1}+{sin}\frac{{A}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$${r}_{{b}} ={r}.\left(\frac{\mathrm{1}+{sin}\frac{{B}}{\mathrm{2}}}{{cos}\frac{{B}}{\mathrm{2}}}\right)^{\mathrm{2}} ,{r}_{{c}} ={r}.\left(\frac{\mathrm{1}+{sin}\frac{{C}}{\mathrm{2}}}{{cos}\frac{{C}}{\mathrm{2}}}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{{r}_{{a}} .{r}_{{b}} }+\sqrt{{r}_{{b}} .{r}_{{c}} }+\sqrt{{r}_{{c}} .{r}_{{a}} }= \\ $$$$={r}.\left[\frac{\left(\mathrm{1}+{sin}\frac{{A}}{\mathrm{2}}\right)\left(\mathrm{1}+{sin}\frac{{B}}{\mathrm{2}}\right)}{{cos}\frac{{A}}{\mathrm{2}}.{cos}\frac{{B}}{\mathrm{2}}}+\frac{\left(\mathrm{1}+{sin}\frac{{B}}{\mathrm{2}}\right)\left(\mathrm{1}+{sin}\frac{{C}}{\mathrm{2}}\right)}{{cos}\frac{{B}}{\mathrm{2}}.{cos}\frac{{C}}{\mathrm{2}}}+\right. \\ $$$$\left.+\frac{\left(\mathrm{1}+{sin}\frac{{A}}{\mathrm{2}}\right)\left(\mathrm{1}+{sin}\frac{{C}}{\mathrm{2}}\right)}{{cos}\frac{{A}}{\mathrm{2}}.{cos}\frac{{C}}{\mathrm{2}}}\right]= \\ $$$$={r}.\left[\frac{{cos}\frac{{C}}{\mathrm{2}}+{cos}\frac{{C}}{\mathrm{2}}{sin}\frac{{A}}{\mathrm{2}}+{cos}\frac{{C}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}+{cos}\frac{{C}}{\mathrm{2}}{sin}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}{cos}\frac{{C}}{\mathrm{2}}}+\right. \\ $$$$+\frac{{cos}\frac{{A}}{\mathrm{2}}+{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}+{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}+{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}{cos}\frac{{C}}{\mathrm{2}}}+ \\ $$$$\left.+\frac{{cos}\frac{{B}}{\mathrm{2}}+{cos}\frac{{B}}{\mathrm{2}}{sin}\frac{{A}}{\mathrm{2}}+{cos}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}+{cos}\frac{{B}}{\mathrm{2}}{sin}\frac{{A}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}}{{cos}\frac{{A}}{\mathrm{2}}{cos}\frac{{B}}{\mathrm{2}}{cos}\frac{{C}}{\mathrm{2}}}\right]= \\ $$$$={r}.\left[\frac{\Sigma{cos}\frac{{A}}{\mathrm{2}}+\Sigma{sin}\frac{{A}+{B}}{\mathrm{2}}+\Sigma{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}}{\Pi{cos}\frac{{A}}{\mathrm{2}}}\right]= \\ $$$$={r}.\left[\frac{\mathrm{2}\Sigma{cos}\frac{{A}}{\mathrm{2}}+\Sigma{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}}{\Pi{cos}\frac{{A}}{\mathrm{2}}}\right]= \\ $$$$\Sigma{cos}\frac{{A}}{\mathrm{2}}{sin}\frac{{B}}{\mathrm{2}}{sin}\frac{{C}}{\mathrm{2}}=\Sigma\sqrt{\frac{{p}\left({p}−{a}\right)}{{bc}}}\sqrt{\frac{\left({p}−{a}\right)\left({p}−{c}\right)\left({p}−{a}\right)\left({p}−{b}\right)}{{ac}.{ab}}}= \\ $$$$=\Sigma\frac{\left({p}−{a}\right).{S}}{{abc}}=\frac{\left(\mathrm{3}{p}−{a}−{b}−{c}\right).{S}}{{abc}}=\frac{{p}.{S}}{\mathrm{4}{R}.{S}}=\frac{{p}}{\mathrm{4}{R}} \\ $$$$\Pi{cos}\frac{{A}}{\mathrm{2}}=\Pi\sqrt{\frac{{p}\left({p}−{a}\right)}{{bc}}}=\frac{{p}.{S}}{{abc}}=\frac{{p}.{S}}{\mathrm{4}{R}.{S}}=\frac{{p}}{\mathrm{4}{R}} \\ $$$$\Rightarrow\Sigma\sqrt{{r}_{{a}} .{r}_{{b}} }={r}.\left(\mathrm{1}+\frac{\mathrm{8}{R}\Sigma{cos}\frac{{A}}{\mathrm{2}}}{{p}}\right) \\ $$$${i}\:{think}\:{there}\:{is}\:{some}\:{thing}\:{wrong}. \\ $$$${please}\:{someone}\:{recheck}\:{my}\:{solution}. \\ $$
