Question Number 164447 by LEKOUMA last updated on 17/Jan/22

Answered by Mathspace last updated on 17/Jan/22
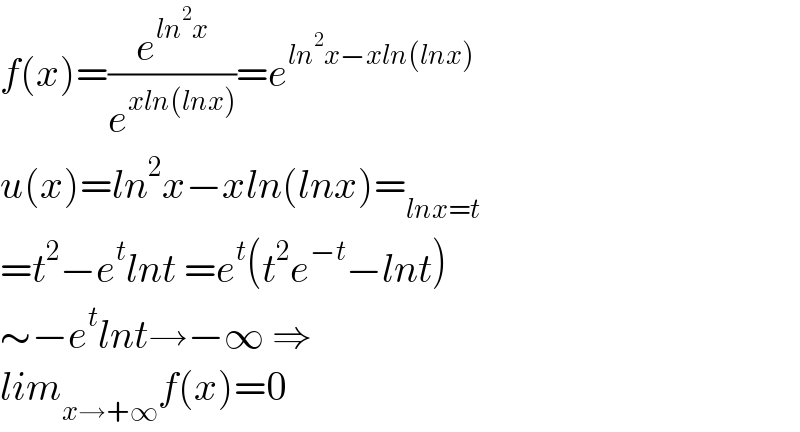
$${f}\left({x}\right)=\frac{{e}^{{ln}^{\mathrm{2}} {x}} }{{e}^{{xln}\left({lnx}\right)} }={e}^{{ln}^{\mathrm{2}} {x}−{xln}\left({lnx}\right)} \\ $$$${u}\left({x}\right)={ln}^{\mathrm{2}} {x}−{xln}\left({lnx}\right)=_{{lnx}={t}} \\ $$$$={t}^{\mathrm{2}} −{e}^{{t}} {lnt}\:={e}^{{t}} \left({t}^{\mathrm{2}} {e}^{−{t}} −{lnt}\right) \\ $$$$\sim−{e}^{{t}} {lnt}\rightarrow−\infty\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\mathrm{0} \\ $$
