Question Number 164468 by ajfour last updated on 17/Jan/22
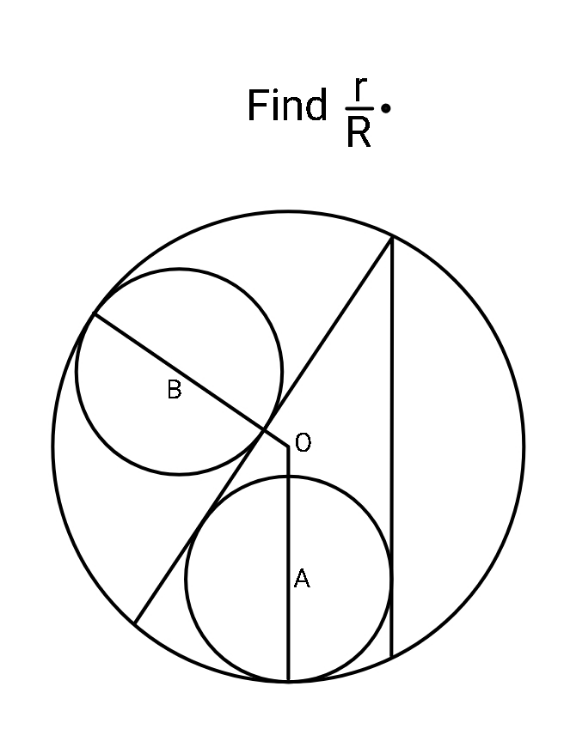
Answered by mr W last updated on 18/Jan/22
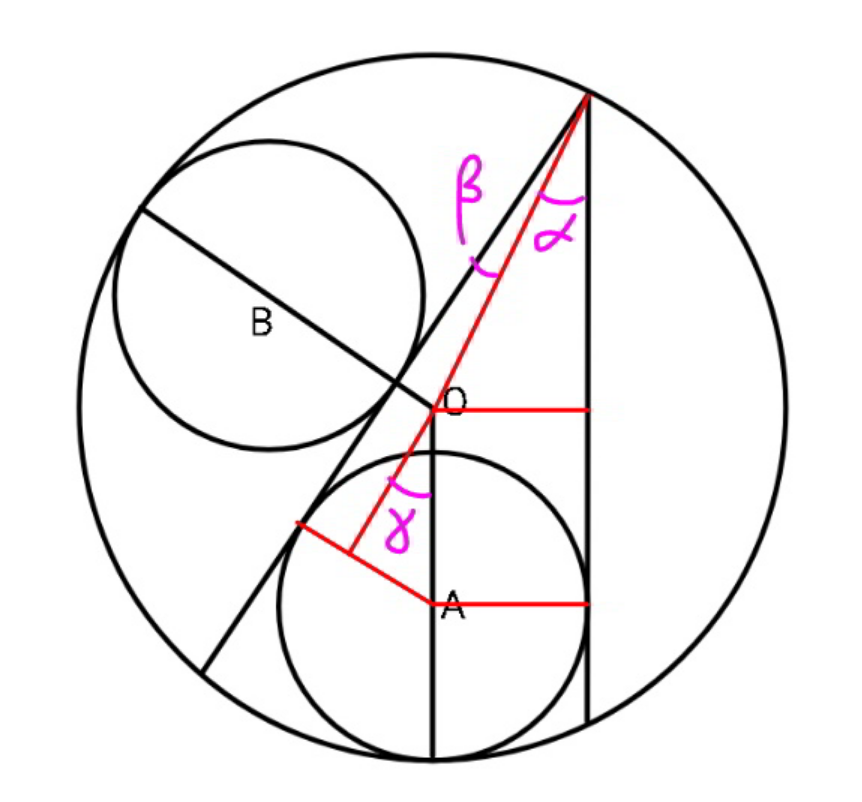
Commented by mr W last updated on 18/Jan/22
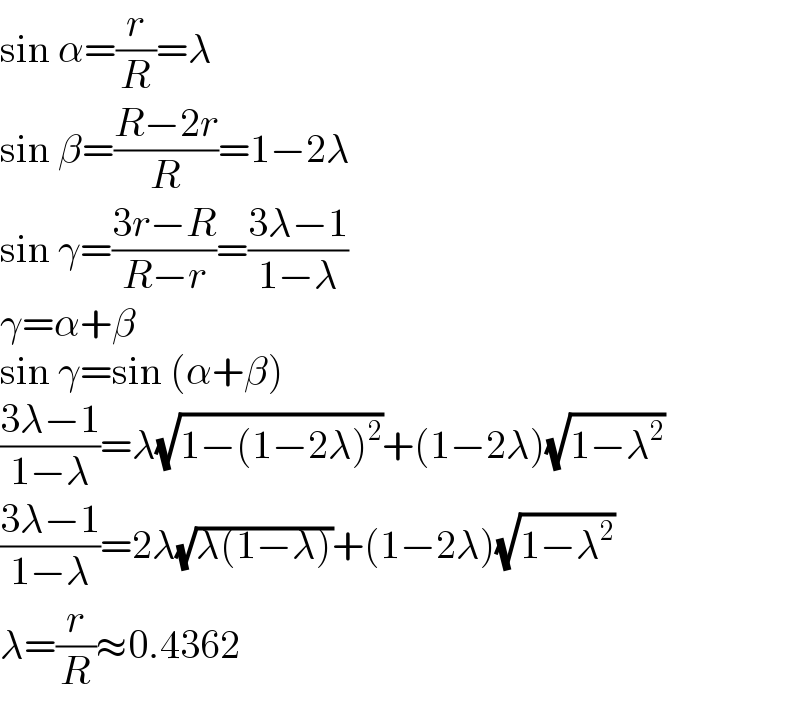
$$\mathrm{sin}\:\alpha=\frac{{r}}{{R}}=\lambda \\ $$$$\mathrm{sin}\:\beta=\frac{{R}−\mathrm{2}{r}}{{R}}=\mathrm{1}−\mathrm{2}\lambda \\ $$$$\mathrm{sin}\:\gamma=\frac{\mathrm{3}{r}−{R}}{{R}−{r}}=\frac{\mathrm{3}\lambda−\mathrm{1}}{\mathrm{1}−\lambda} \\ $$$$\gamma=\alpha+\beta \\ $$$$\mathrm{sin}\:\gamma=\mathrm{sin}\:\left(\alpha+\beta\right) \\ $$$$\frac{\mathrm{3}\lambda−\mathrm{1}}{\mathrm{1}−\lambda}=\lambda\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{2}\lambda\right)^{\mathrm{2}} }+\left(\mathrm{1}−\mathrm{2}\lambda\right)\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\frac{\mathrm{3}\lambda−\mathrm{1}}{\mathrm{1}−\lambda}=\mathrm{2}\lambda\sqrt{\lambda\left(\mathrm{1}−\lambda\right)}+\left(\mathrm{1}−\mathrm{2}\lambda\right)\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} } \\ $$$$\lambda=\frac{{r}}{{R}}\approx\mathrm{0}.\mathrm{4362} \\ $$
Commented by ajfour last updated on 19/Jan/22
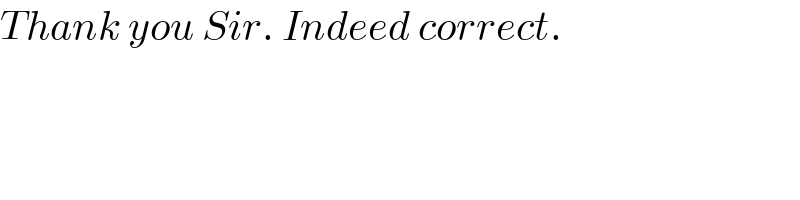
$${Thank}\:{you}\:{Sir}.\:{Indeed}\:{correct}. \\ $$
Commented by mr W last updated on 19/Jan/22
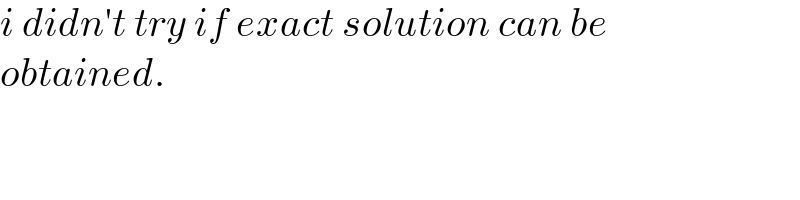
$${i}\:{didn}'{t}\:{try}\:{if}\:{exact}\:{solution}\:{can}\:{be} \\ $$$${obtained}. \\ $$
Commented by mr W last updated on 18/Jan/22

Answered by ajfour last updated on 20/Jan/22
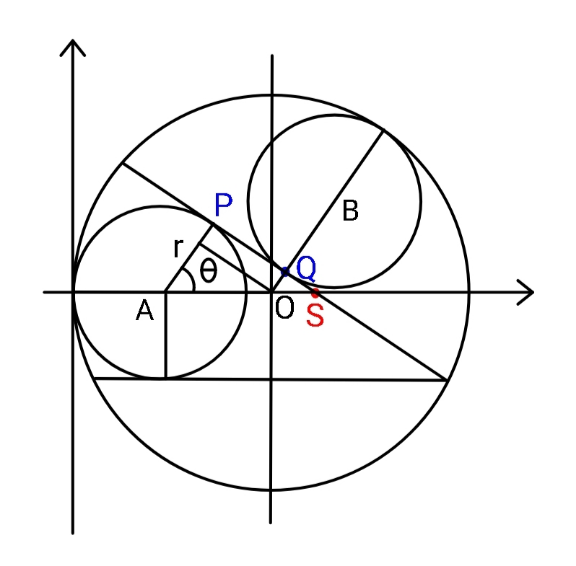
Commented by ajfour last updated on 21/Jan/22
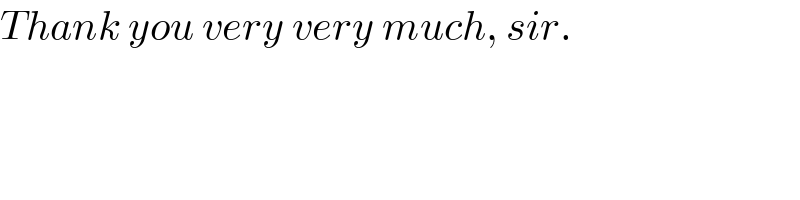
$${Thank}\:{you}\:{very}\:{very}\:{much},\:{sir}. \\ $$
Commented by ajfour last updated on 21/Jan/22
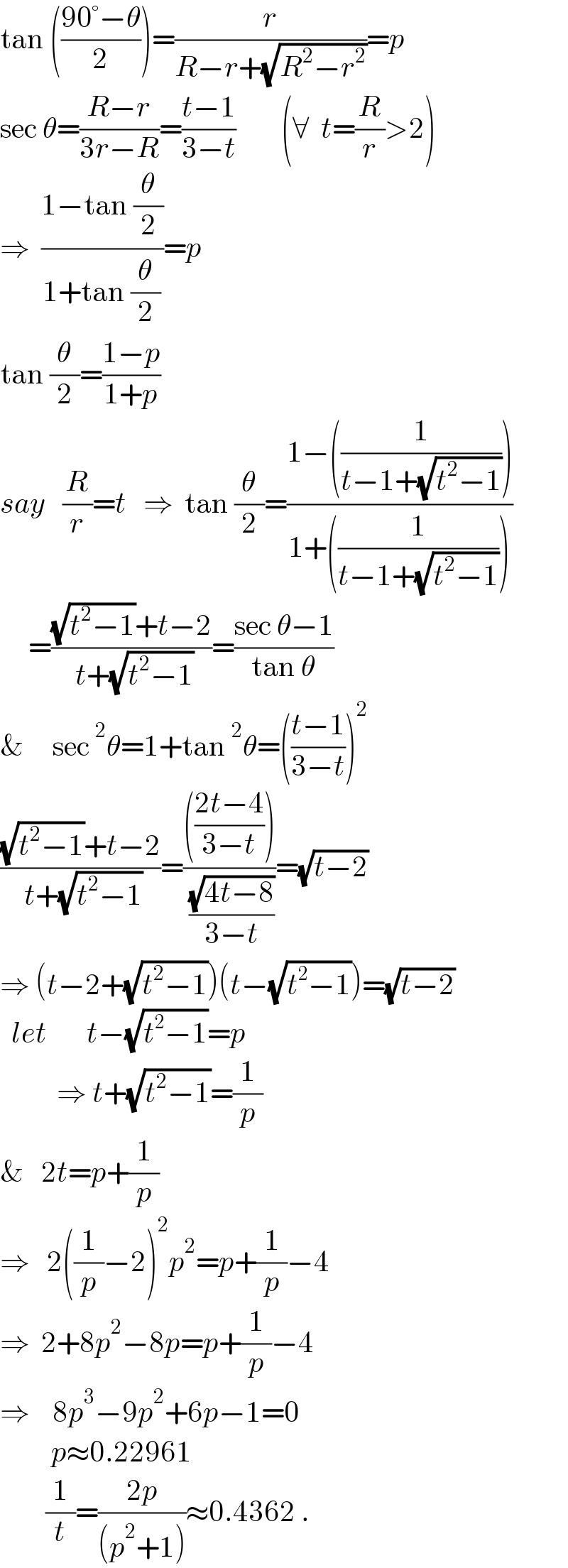
$$\mathrm{tan}\:\left(\frac{\mathrm{90}°−\theta}{\mathrm{2}}\right)=\frac{{r}}{{R}−{r}+\sqrt{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }}={p} \\ $$$$\mathrm{sec}\:\theta=\frac{{R}−{r}}{\mathrm{3}{r}−{R}}=\frac{{t}−\mathrm{1}}{\mathrm{3}−{t}}\:\:\:\:\:\:\:\:\left(\forall\:\:{t}=\frac{{R}}{{r}}>\mathrm{2}\right) \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}−\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{1}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}={p} \\ $$$$\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}−{p}}{\mathrm{1}+{p}}\:\:\: \\ $$$${say}\:\:\:\frac{{R}}{{r}}={t}\:\:\:\Rightarrow\:\:\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\frac{\mathrm{1}−\left(\frac{\mathrm{1}}{{t}−\mathrm{1}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\right)}{\mathrm{1}+\left(\frac{\mathrm{1}}{{t}−\mathrm{1}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}\right)} \\ $$$$\:\:\:\:\:=\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}+{t}−\mathrm{2}}{\:{t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\frac{\mathrm{sec}\:\theta−\mathrm{1}}{\mathrm{tan}\:\theta} \\ $$$$\&\:\:\:\:\:\mathrm{sec}\:^{\mathrm{2}} \theta=\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \theta=\left(\frac{{t}−\mathrm{1}}{\mathrm{3}−{t}}\right)^{\mathrm{2}} \\ $$$$\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}+{t}−\mathrm{2}}{\:{t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}=\frac{\left(\frac{\mathrm{2}{t}−\mathrm{4}}{\mathrm{3}−{t}}\right)}{\:\frac{\sqrt{\mathrm{4}{t}−\mathrm{8}}}{\mathrm{3}−{t}}}=\sqrt{{t}−\mathrm{2}} \\ $$$$\Rightarrow\:\left({t}−\mathrm{2}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)\left({t}−\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\right)=\sqrt{{t}−\mathrm{2}} \\ $$$$\:\:{let}\:\:\:\:\:\:\:{t}−\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}={p} \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{t}+\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{{p}} \\ $$$$\&\:\:\:\mathrm{2}{t}={p}+\frac{\mathrm{1}}{{p}} \\ $$$$\Rightarrow\:\:\:\mathrm{2}\left(\frac{\mathrm{1}}{{p}}−\mathrm{2}\right)^{\mathrm{2}} {p}^{\mathrm{2}} ={p}+\frac{\mathrm{1}}{{p}}−\mathrm{4} \\ $$$$\Rightarrow\:\:\mathrm{2}+\mathrm{8}{p}^{\mathrm{2}} −\mathrm{8}{p}={p}+\frac{\mathrm{1}}{{p}}−\mathrm{4} \\ $$$$\Rightarrow\:\:\:\:\mathrm{8}{p}^{\mathrm{3}} −\mathrm{9}{p}^{\mathrm{2}} +\mathrm{6}{p}−\mathrm{1}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:{p}\approx\mathrm{0}.\mathrm{22961} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{t}}=\frac{\mathrm{2}{p}}{\left({p}^{\mathrm{2}} +\mathrm{1}\right)}\approx\mathrm{0}.\mathrm{4362}\:. \\ $$
Commented by mr W last updated on 21/Jan/22
$${great}!\:{one}\:{can}\:{even}\:{get}\:{exact}\:{value}\:{of} \\ $$$${p}! \\ $$
