Question Number 164530 by hoochhoch last updated on 18/Jan/22

Commented by Rasheed.Sindhi last updated on 18/Jan/22
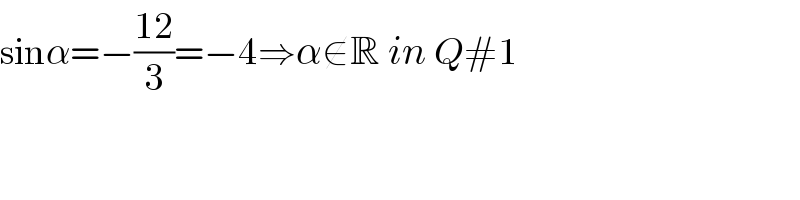
$$\mathrm{sin}\alpha=−\frac{\mathrm{12}}{\mathrm{3}}=−\mathrm{4}\Rightarrow\alpha\notin\mathbb{R}\:{in}\:{Q}#\mathrm{1} \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jan/22

$$\mathrm{sin}\alpha=\frac{\mathrm{3}}{\mathrm{5}}\:;\frac{\mathrm{cot}\alpha+\mathrm{tan}\alpha\:\:}{\mathrm{cot}\alpha−\mathrm{tan}\alpha}=? \\ $$$$\frac{\mathrm{cot}\alpha+\mathrm{tan}\alpha\:\:}{\mathrm{cot}\alpha−\mathrm{tan}\alpha}=\frac{\frac{\mathrm{cos}\alpha\:}{\mathrm{sin}\alpha\:}+\frac{\mathrm{sin}\alpha\:}{\mathrm{cos}\alpha\:}}{\frac{\mathrm{cos}\alpha\:}{\mathrm{sin}\alpha\:}−\frac{\mathrm{sin}\alpha\:}{\mathrm{cos}\alpha\:}} \\ $$$$=\frac{\mathrm{cos}^{\mathrm{2}} \alpha+\mathrm{sin}^{\mathrm{2}} \alpha\:\:}{\mathrm{cos}^{\mathrm{2}} \alpha−\mathrm{sin}^{\mathrm{2}} \alpha}=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2sin}^{\mathrm{2}} \alpha\:} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}−\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\frac{\mathrm{25}−\mathrm{18}}{\mathrm{25}}}=\frac{\mathrm{25}}{\mathrm{7}} \\ $$
