Question Number 164576 by mathlove last updated on 19/Jan/22

Answered by Rasheed.Sindhi last updated on 19/Jan/22
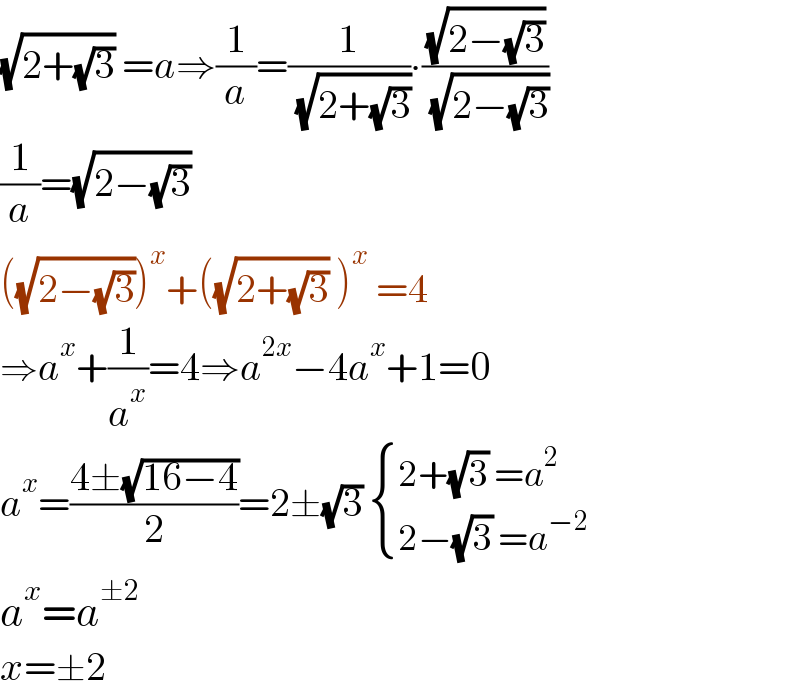
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:={a}\Rightarrow\frac{\mathrm{1}}{{a}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}\centerdot\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}} \\ $$$$\frac{\mathrm{1}}{{a}}=\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\: \\ $$$$\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{{x}} +\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \:=\mathrm{4} \\ $$$$\Rightarrow{a}^{{x}} +\frac{\mathrm{1}}{{a}^{{x}} }=\mathrm{4}\Rightarrow{a}^{\mathrm{2}{x}} −\mathrm{4}{a}^{{x}} +\mathrm{1}=\mathrm{0} \\ $$$${a}^{{x}} =\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}}\:\begin{cases}{\mathrm{2}+\sqrt{\mathrm{3}}\:={a}^{\mathrm{2}} }\\{\mathrm{2}−\sqrt{\mathrm{3}}\:={a}^{−\mathrm{2}} }\end{cases} \\ $$$${a}^{{x}} ={a}^{\pm\mathrm{2}} \: \\ $$$${x}=\pm\mathrm{2} \\ $$
