Question Number 164626 by amin96 last updated on 19/Jan/22
Commented by mr W last updated on 19/Jan/22

$$\left.\Rightarrow\:{C}\right) \\ $$
Answered by mr W last updated on 20/Jan/22

Commented by mr W last updated on 20/Jan/22

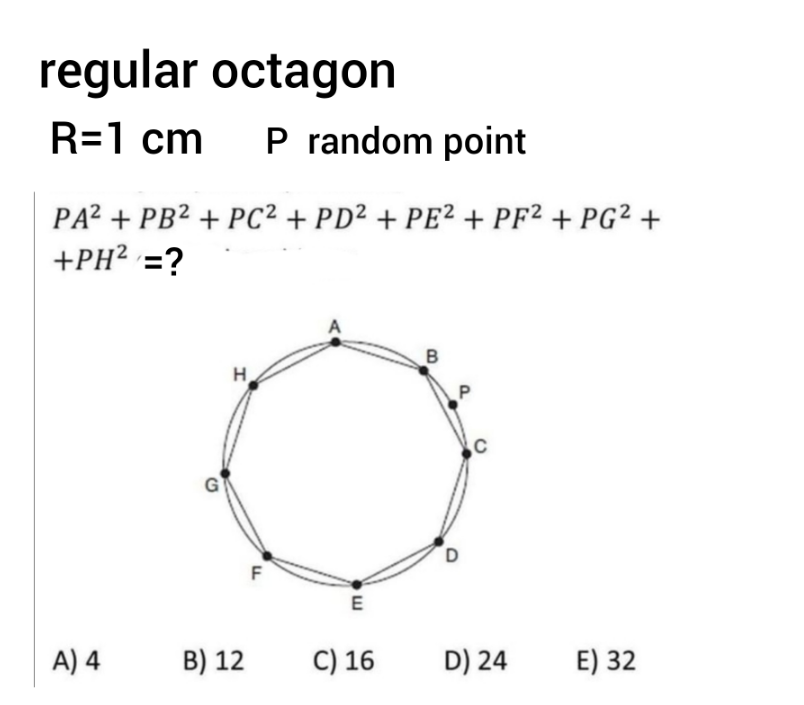
$${say}\:{we}\:{have}\:{a}\:{regular}\:{polygon}\:{with} \\ $$$${n}\:{sides}. \\ $$$${R}={radius} \\ $$$${a}={side}\:{length} \\ $$$$\alpha=\frac{\pi}{{n}} \\ $$$${a}=\mathrm{2}{R}\:\mathrm{sin}\:\alpha \\ $$$$ \\ $$$${let}\:{d}_{{i}} ={PP}_{{i}} \\ $$$${a}^{\mathrm{2}} ={d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} −\mathrm{2}{d}_{\mathrm{1}} {d}_{\mathrm{2}} \:\mathrm{cos}\:\alpha \\ $$$${a}^{\mathrm{2}} ={d}_{\mathrm{2}} ^{\mathrm{2}} +{d}_{\mathrm{3}} ^{\mathrm{2}} −\mathrm{2}{d}_{\mathrm{2}} {d}_{\mathrm{3}} \:\mathrm{cos}\:\alpha \\ $$$$… \\ $$$${a}^{\mathrm{2}} ={d}_{{n}−\mathrm{1}} ^{\mathrm{2}} +{d}_{{n}} ^{\mathrm{2}} −\mathrm{2}{d}_{{n}−\mathrm{1}} {d}_{{n}} \:\mathrm{cos}\:\alpha \\ $$$${a}^{\mathrm{2}} ={d}_{{n}} ^{\mathrm{2}} +{d}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{2}{d}_{{n}} {d}_{\mathrm{1}} \:\mathrm{cos}\:\left({n}−\mathrm{1}\right)\alpha\:\:\:\leftarrow\:\mathrm{cos}\:\left({n}−\mathrm{1}\right)\alpha=\mathrm{cos}\:\left(\pi−\alpha\right)=−\mathrm{cos}\:\alpha \\ $$$$\Sigma: \\ $$$${na}^{\mathrm{2}} =\mathrm{2}\left({d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} \right)−\mathrm{2}\left({d}_{\mathrm{1}} {d}_{\mathrm{2}} +{d}_{\mathrm{2}} {d}_{\mathrm{3}} +…+{d}_{{n}−\mathrm{1}} {d}_{{n}} −{d}_{{n}} {d}_{\mathrm{1}} \right)\mathrm{cos}\:\alpha \\ $$$${na}^{\mathrm{2}} =\mathrm{2}\left({d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{2}}\left({d}_{\mathrm{1}} {d}_{\mathrm{2}} +{d}_{\mathrm{2}} {d}_{\mathrm{3}} +…+{d}_{{n}−\mathrm{1}} {d}_{{n}} −{d}_{{n}} {d}_{\mathrm{1}} \right)\mathrm{sin}\:\:\alpha×\frac{\mathrm{4}}{\mathrm{tan}\:\alpha} \\ $$$${na}^{\mathrm{2}} =\mathrm{2}\left({d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} \right)−{A}_{{polygon}} ×\frac{\mathrm{4}}{\mathrm{tan}\:\alpha} \\ $$$${d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} =\frac{{n}}{\mathrm{2}}{a}^{\mathrm{2}} +\frac{\mathrm{2}{A}_{{polygon}} }{\mathrm{tan}\:\alpha} \\ $$$${A}_{{polygon}} ={n}×\frac{{R}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}}=\frac{{nR}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{sin}\:\mathrm{2}\alpha \\ $$$${d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} =\frac{{n}}{\mathrm{2}}×\mathrm{4}{R}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+\frac{\mathrm{2}{nR}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\alpha}{\mathrm{2}\:\mathrm{tan}\:\alpha} \\ $$$${d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} =\mathrm{2}{nR}^{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\alpha+\mathrm{2}{nR}^{\mathrm{2}} \:\mathrm{cos}^{\mathrm{2}} \:\alpha \\ $$$$\Rightarrow{d}_{\mathrm{1}} ^{\mathrm{2}} +{d}_{\mathrm{2}} ^{\mathrm{2}} +…+{d}_{{n}} ^{\mathrm{2}} =\mathrm{2}{nR}^{\mathrm{2}} \\ $$$${generally}\:{for}\:{regular}\:{n}−{side}\:{polygon}: \\ $$$$\begin{array}{|c|}{{PP}_{\mathrm{1}} ^{\mathrm{2}} +{PP}_{\mathrm{2}} ^{\mathrm{2}} +…+{PP}_{{n}} ^{\mathrm{2}} =\mathrm{2}{nR}^{\mathrm{2}} }\\\hline\end{array} \\ $$$${in}\:{case}\:{of}\:{octagon}: \\ $$$${n}=\mathrm{8}\:,\:{R}=\mathrm{1} \\ $$$${PA}^{\mathrm{2}} +{PB}^{\mathrm{2}} +…+{PH}^{\mathrm{2}} =\mathrm{2}×\mathrm{8}×\mathrm{1}^{\mathrm{2}} =\mathrm{16} \\ $$
Commented by Tawa11 last updated on 19/Jan/22
$$\mathrm{Weldone}\:\mathrm{sir}.\:\mathrm{Great} \\ $$
Commented by amin96 last updated on 20/Jan/22

$$\boldsymbol{\mathrm{bravo}}\:\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{nice}}\:\boldsymbol{\mathrm{solution}} \\ $$
