Question Number 16464 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17
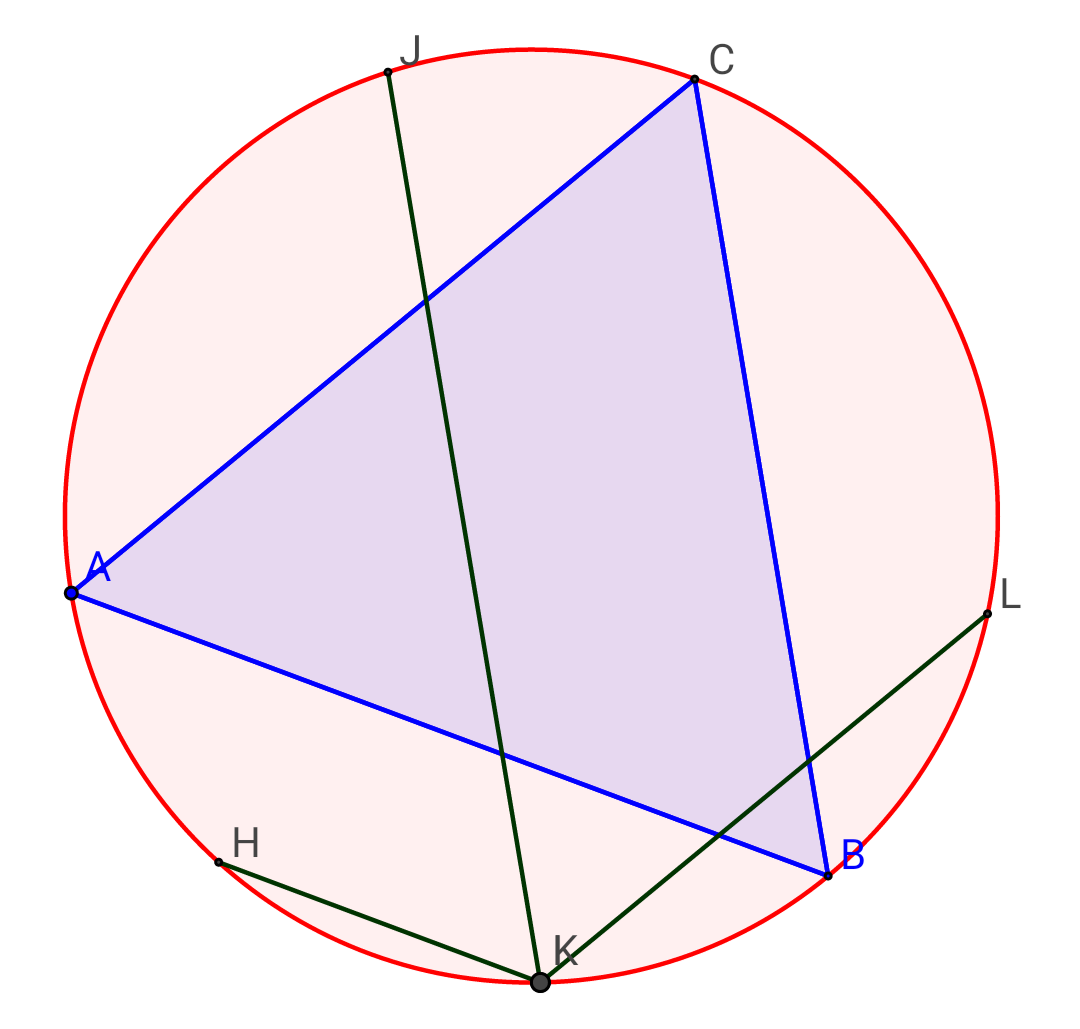
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 22/Jun/17

$${A}\overset{\Delta} {{B}C},{is}\:{equilateral}\:{and}\:'{K}'\:{is}\:{a}\:{point} \\ $$$${on}\:{circumcircle}\:\:{of}\:{it}.{draw}\:{KH},{KJ},{KL} \\ $$$${parallel}\:{to}\:{ABC}'{s}\:{sides}\:{as}\:{showen}. \\ $$$$\left.\mathrm{1}\right){prove}\:{that}: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{KJ}={KH}+{KL}\: \\ $$$$\left.\mathrm{2}\right){drawing}\:{KL}\:\&\:{KJ},\:{makes}\:\mathrm{3}\:{regions} \\ $$$${in}\:{triangle}\:{ABC},{that}\:{we}\:{name}\:{this}\: \\ $$$${regions}\:{as}:\:{S}_{\mathrm{1}} <{S}_{\mathrm{2}} <{S}_{\mathrm{3}} .{find}\:{maximum} \\ $$$${of}\:{ratio}:\frac{{S}_{\mathrm{3}} }{{S}_{\mathrm{1}} +{S}_{\mathrm{2}} },{when}\:'{K}',{moves}\:{from} \\ $$$$\overset{} {{m}idpoint}\:{of}\:\overset{} {{K}B}\:{to}\:{midpoint}\:{of}\:{KA}. \\ $$$${S}_{\mathrm{1}} ={area}\:{of}\:{region}\:{no}.\mathrm{1} \\ $$
Commented by mrW1 last updated on 23/Jun/17
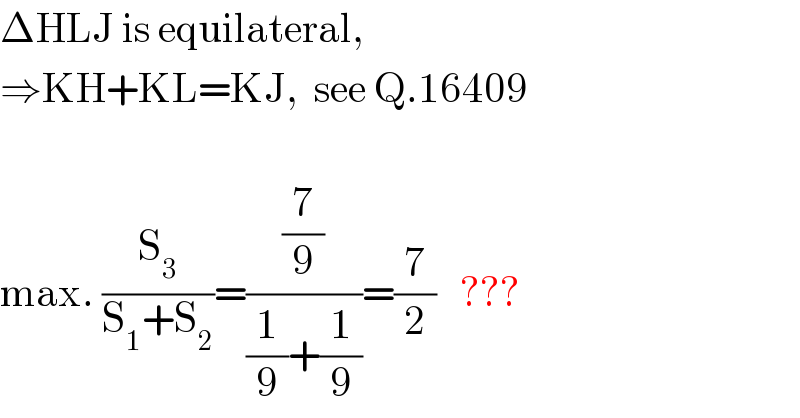
$$\Delta\mathrm{HLJ}\:\mathrm{is}\:\mathrm{equilateral},\: \\ $$$$\Rightarrow\mathrm{KH}+\mathrm{KL}=\mathrm{KJ},\:\:\mathrm{see}\:\mathrm{Q}.\mathrm{16409} \\ $$$$ \\ $$$$\mathrm{max}.\:\frac{\mathrm{S}_{\mathrm{3}} }{\mathrm{S}_{\mathrm{1}} +\mathrm{S}_{\mathrm{2}} }=\frac{\frac{\mathrm{7}}{\mathrm{9}}}{\frac{\mathrm{1}}{\mathrm{9}}+\frac{\mathrm{1}}{\mathrm{9}}}=\frac{\mathrm{7}}{\mathrm{2}}\:\:\:??? \\ $$
