Question Number 16466 by tawa tawa last updated on 22/Jun/17

Answered by sandy_suhendra last updated on 22/Jun/17

Commented by sandy_suhendra last updated on 22/Jun/17
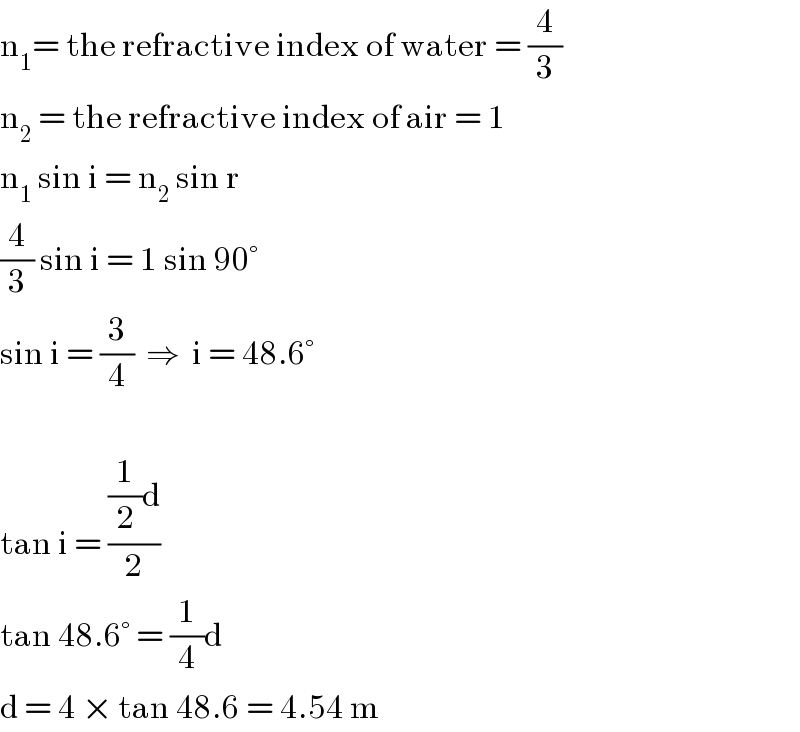
$$\mathrm{n}_{\mathrm{1}} =\:\mathrm{the}\:\mathrm{refractive}\:\mathrm{index}\:\mathrm{of}\:\mathrm{water}\:=\:\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\mathrm{n}_{\mathrm{2}} \:=\:\mathrm{the}\:\mathrm{refractive}\:\mathrm{index}\:\mathrm{of}\:\mathrm{air}\:=\:\mathrm{1} \\ $$$$\mathrm{n}_{\mathrm{1}} \:\mathrm{sin}\:\mathrm{i}\:=\:\mathrm{n}_{\mathrm{2}} \:\mathrm{sin}\:\mathrm{r} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}\:\mathrm{sin}\:\mathrm{i}\:=\:\mathrm{1}\:\mathrm{sin}\:\mathrm{90}° \\ $$$$\mathrm{sin}\:\mathrm{i}\:=\:\frac{\mathrm{3}}{\mathrm{4}}\:\:\Rightarrow\:\:\mathrm{i}\:=\:\mathrm{48}.\mathrm{6}° \\ $$$$ \\ $$$$\mathrm{tan}\:\mathrm{i}\:=\:\frac{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{d}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\mathrm{48}.\mathrm{6}°\:=\:\frac{\mathrm{1}}{\mathrm{4}}\mathrm{d}\: \\ $$$$\mathrm{d}\:=\:\mathrm{4}\:×\:\mathrm{tan}\:\mathrm{48}.\mathrm{6}\:=\:\mathrm{4}.\mathrm{54}\:\mathrm{m} \\ $$
Commented by tawa tawa last updated on 22/Jun/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
