Question Number 164787 by cortano1 last updated on 22/Jan/22

Answered by mr W last updated on 22/Jan/22
![xy[(x+y)^2 −2xy]=((10(x+y)^2 )/9) xy[(x+y)^3 −3xy(x+y)]=((2(x+y)^3 )/3) let u=x+y, v=xy { ((v(u^2 −2v)=((10u^2 )/9) ...(i))),((vu(u^2 −3v)=((2u^3 )/3) ...(ii))) :} from (ii): u=0 ⇒v=0 ⇒x=y=0 or u≠0 ⇒v≠0 v(u^2 −3v)=((2u^2 )/3) ...(iii) (i)/(ii): ((u^2 −2v)/(u^2 −3v))=(5/3) 2u^2 =9v ⇒v=((2u^2 )/9) put this into (iii): ((2u^2 )/9)(u^2 −3×((2u^2 )/9))=((2u^2 )/3) u^2 =9 ⇒u=±3 ⇒v=2 x,y are roots of z^2 −uz+v=0 x,y=((u±(√(u^2 −4v)))/2)=((±3±1)/2)=2, 1 or −2,−1 summary: (x,y)=(0,0), (−2,−1),(−1,−2),(2,1),(1,2)](https://www.tinkutara.com/question/Q164789.png)
$${xy}\left[\left({x}+{y}\right)^{\mathrm{2}} −\mathrm{2}{xy}\right]=\frac{\mathrm{10}\left({x}+{y}\right)^{\mathrm{2}} }{\mathrm{9}} \\ $$$${xy}\left[\left({x}+{y}\right)^{\mathrm{3}} −\mathrm{3}{xy}\left({x}+{y}\right)\right]=\frac{\mathrm{2}\left({x}+{y}\right)^{\mathrm{3}} }{\mathrm{3}} \\ $$$${let}\:{u}={x}+{y},\:{v}={xy} \\ $$$$\begin{cases}{{v}\left({u}^{\mathrm{2}} −\mathrm{2}{v}\right)=\frac{\mathrm{10}{u}^{\mathrm{2}} }{\mathrm{9}}\:\:\:…\left({i}\right)}\\{{vu}\left({u}^{\mathrm{2}} −\mathrm{3}{v}\right)=\frac{\mathrm{2}{u}^{\mathrm{3}} }{\mathrm{3}}\:\:\:…\left({ii}\right)}\end{cases} \\ $$$${from}\:\left({ii}\right): \\ $$$${u}=\mathrm{0} \\ $$$$\Rightarrow{v}=\mathrm{0} \\ $$$$\Rightarrow{x}={y}=\mathrm{0} \\ $$$${or} \\ $$$${u}\neq\mathrm{0}\:\Rightarrow{v}\neq\mathrm{0} \\ $$$${v}\left({u}^{\mathrm{2}} −\mathrm{3}{v}\right)=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{3}}\:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)/\left({ii}\right): \\ $$$$\frac{{u}^{\mathrm{2}} −\mathrm{2}{v}}{{u}^{\mathrm{2}} −\mathrm{3}{v}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\mathrm{2}{u}^{\mathrm{2}} =\mathrm{9}{v} \\ $$$$\Rightarrow{v}=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${put}\:{this}\:{into}\:\left({iii}\right): \\ $$$$\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}}\left({u}^{\mathrm{2}} −\mathrm{3}×\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{9}}\right)=\frac{\mathrm{2}{u}^{\mathrm{2}} }{\mathrm{3}} \\ $$$${u}^{\mathrm{2}} =\mathrm{9} \\ $$$$\Rightarrow{u}=\pm\mathrm{3} \\ $$$$\Rightarrow{v}=\mathrm{2} \\ $$$${x},{y}\:{are}\:{roots}\:{of}\:{z}^{\mathrm{2}} −{uz}+{v}=\mathrm{0} \\ $$$${x},{y}=\frac{{u}\pm\sqrt{{u}^{\mathrm{2}} −\mathrm{4}{v}}}{\mathrm{2}}=\frac{\pm\mathrm{3}\pm\mathrm{1}}{\mathrm{2}}=\mathrm{2},\:\mathrm{1}\:{or}\:−\mathrm{2},−\mathrm{1} \\ $$$${summary}: \\ $$$$\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right),\:\left(−\mathrm{2},−\mathrm{1}\right),\left(−\mathrm{1},−\mathrm{2}\right),\left(\mathrm{2},\mathrm{1}\right),\left(\mathrm{1},\mathrm{2}\right) \\ $$
Commented by leonhard77 last updated on 22/Jan/22

$$\left({i}\right):\left({ii}\right)\Rightarrow\frac{\mathrm{5}}{\mathrm{3}{u}} \\ $$
Commented by mr W last updated on 22/Jan/22
$${you}\:{should}\:{look}\:{at}\:{both}\:{sides}! \\ $$
Commented by cortano1 last updated on 22/Jan/22

Commented by Tawa11 last updated on 22/Jan/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by MJS_new last updated on 22/Jan/22
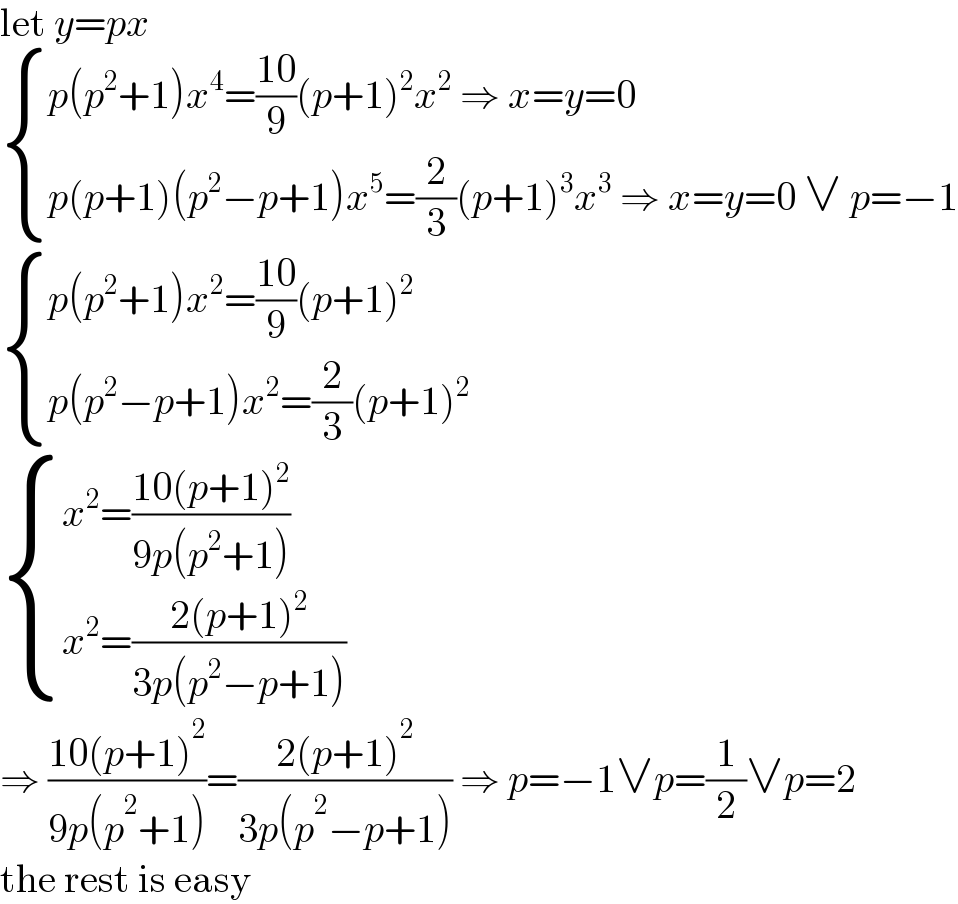
$$\mathrm{let}\:{y}={px} \\ $$$$\begin{cases}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{4}} =\frac{\mathrm{10}}{\mathrm{9}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{2}} \:\Rightarrow\:{x}={y}=\mathrm{0}}\\{{p}\left({p}+\mathrm{1}\right)\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right){x}^{\mathrm{5}} =\frac{\mathrm{2}}{\mathrm{3}}\left({p}+\mathrm{1}\right)^{\mathrm{3}} {x}^{\mathrm{3}} \:\Rightarrow\:{x}={y}=\mathrm{0}\:\vee\:{p}=−\mathrm{1}}\end{cases} \\ $$$$\begin{cases}{{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right){x}^{\mathrm{2}} =\frac{\mathrm{10}}{\mathrm{9}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }\\{{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right){x}^{\mathrm{2}} =\frac{\mathrm{2}}{\mathrm{3}}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }\end{cases} \\ $$$$\begin{cases}{{x}^{\mathrm{2}} =\frac{\mathrm{10}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}}\\{{x}^{\mathrm{2}} =\frac{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)}}\end{cases} \\ $$$$\Rightarrow\:\frac{\mathrm{10}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{9}{p}\left({p}^{\mathrm{2}} +\mathrm{1}\right)}=\frac{\mathrm{2}\left({p}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}{p}\left({p}^{\mathrm{2}} −{p}+\mathrm{1}\right)}\:\Rightarrow\:{p}=−\mathrm{1}\vee{p}=\frac{\mathrm{1}}{\mathrm{2}}\vee{p}=\mathrm{2} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
