Question Number 164793 by bekzodjumayev last updated on 22/Jan/22
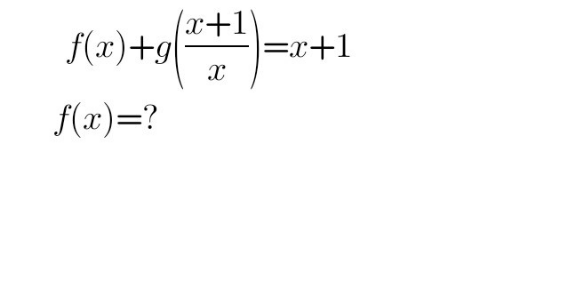
Commented by bekzodjumayev last updated on 22/Jan/22

$${Help} \\ $$
Commented by mr W last updated on 22/Jan/22

$${no}\:{unique}\:{solution}\:{possible}!\: \\ $$$${there}\:{are}\:{two}\:{unknown}\:{functions}! \\ $$$${you}\:{can}\:{only}\:{get}\:{f}\left({x}\right)={x}+\mathrm{1}−{g}\left(\frac{{x}+\mathrm{1}}{{x}}\right). \\ $$$${maybe}\:{you}\:{mean}\:{f}\left({x}\right)+{f}\left(\frac{{x}+\mathrm{1}}{{x}}\right)={x}+\mathrm{1}? \\ $$
Commented by bekzodjumayev last updated on 22/Jan/22
$${Understood}\:{thank}\:{you} \\ $$
Answered by qaz last updated on 22/Jan/22
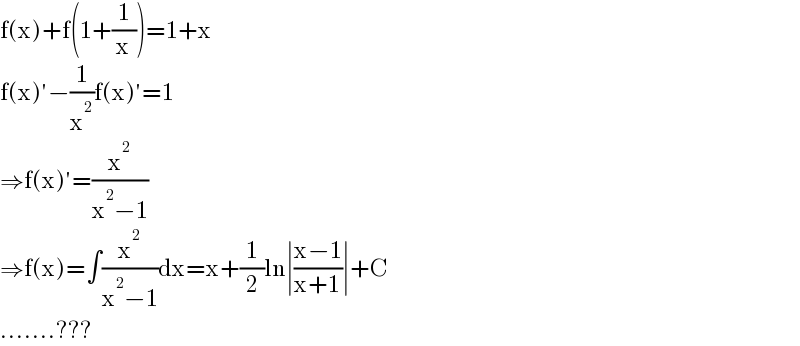
$$\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{x}}\right)=\mathrm{1}+\mathrm{x} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)'−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{f}\left(\mathrm{x}\right)'=\mathrm{1} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)'=\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\Rightarrow\mathrm{f}\left(\mathrm{x}\right)=\int\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{x}^{\mathrm{2}} −\mathrm{1}}\mathrm{dx}=\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{1}}{\mathrm{x}+\mathrm{1}}\mid+\mathrm{C} \\ $$$$…….??? \\ $$
