Question Number 164795 by HongKing last updated on 22/Jan/22
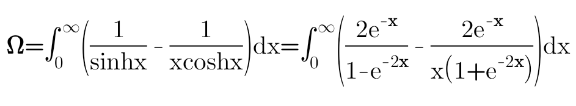
Answered by puissant last updated on 22/Jan/22
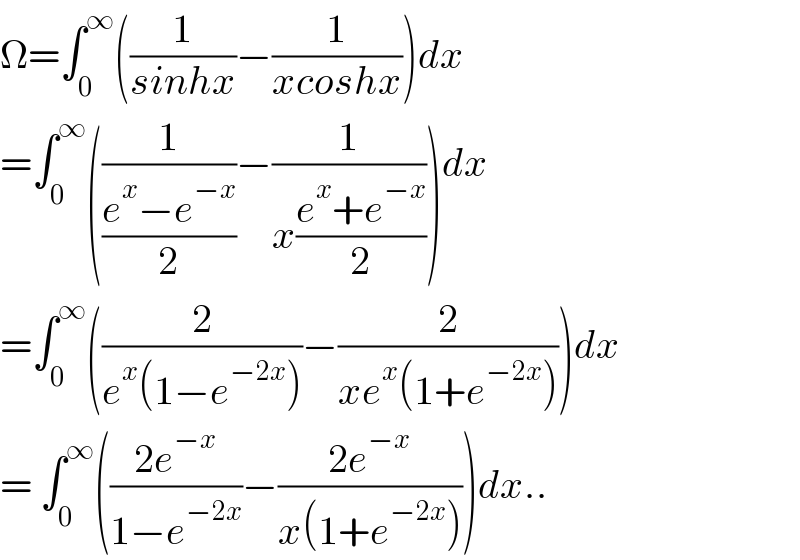
$$\Omega=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{{sinhx}}−\frac{\mathrm{1}}{{xcoshx}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\frac{{e}^{{x}} −{e}^{−{x}} }{\mathrm{2}}}−\frac{\mathrm{1}}{{x}\frac{{e}^{{x}} +{e}^{−{x}} }{\mathrm{2}}}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{2}}{{e}^{{x}} \left(\mathrm{1}−{e}^{−\mathrm{2}{x}} \right)}−\frac{\mathrm{2}}{{xe}^{{x}} \left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)}\right){dx} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{2}{e}^{−{x}} }{\mathrm{1}−{e}^{−\mathrm{2}{x}} }−\frac{\mathrm{2}{e}^{−{x}} }{{x}\left(\mathrm{1}+{e}^{−\mathrm{2}{x}} \right)}\right){dx}.. \\ $$
