Question Number 164808 by Mathematification last updated on 22/Jan/22
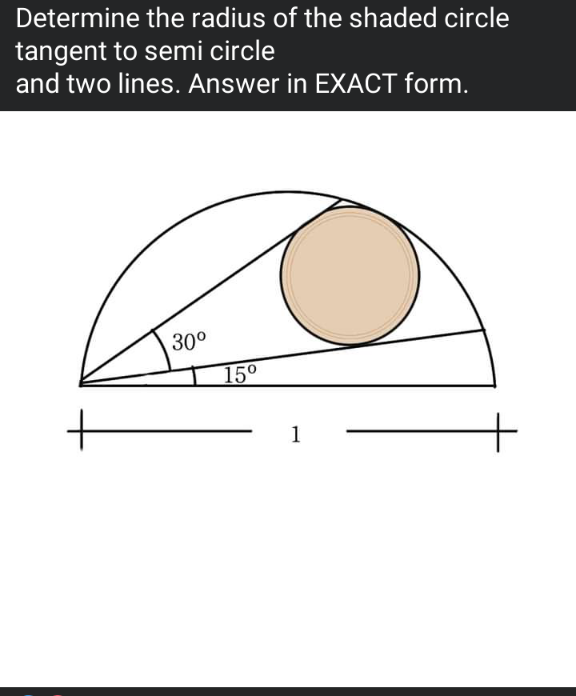
Answered by mr W last updated on 22/Jan/22
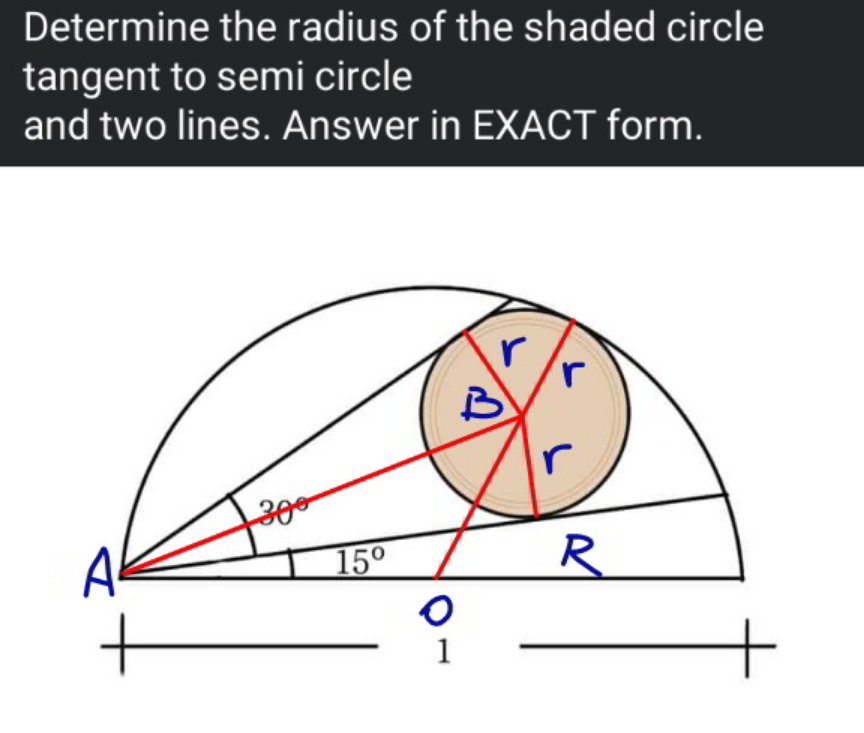
Commented by mr W last updated on 22/Jan/22
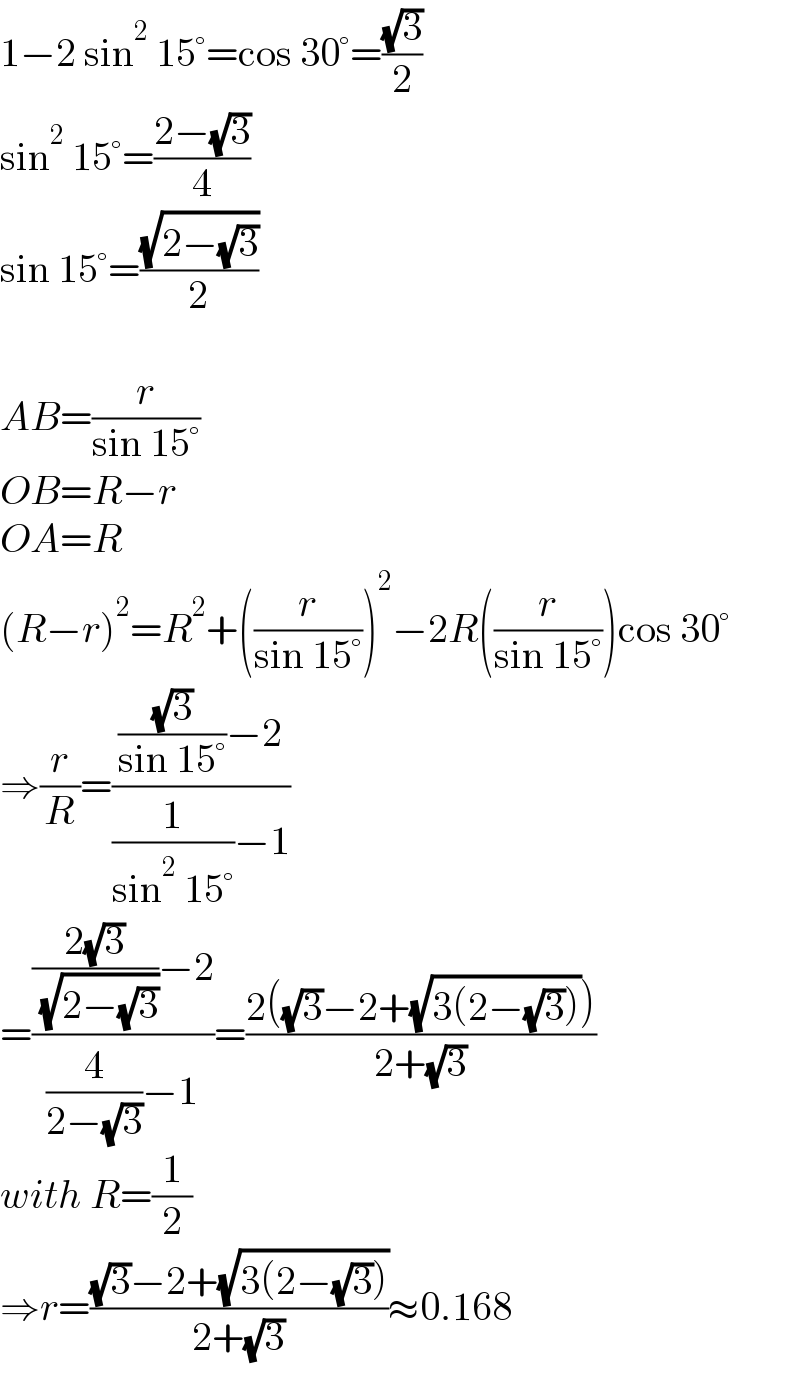
$$\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\mathrm{15}°=\mathrm{cos}\:\mathrm{30}°=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\mathrm{15}°=\frac{\mathrm{2}−\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\mathrm{15}°=\frac{\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}{\mathrm{2}} \\ $$$$ \\ $$$${AB}=\frac{{r}}{\mathrm{sin}\:\mathrm{15}°} \\ $$$${OB}={R}−{r} \\ $$$${OA}={R} \\ $$$$\left({R}−{r}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} +\left(\frac{{r}}{\mathrm{sin}\:\mathrm{15}°}\right)^{\mathrm{2}} −\mathrm{2}{R}\left(\frac{{r}}{\mathrm{sin}\:\mathrm{15}°}\right)\mathrm{cos}\:\mathrm{30}° \\ $$$$\Rightarrow\frac{{r}}{{R}}=\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{sin}\:\mathrm{15}°}−\mathrm{2}}{\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \:\mathrm{15}°}−\mathrm{1}} \\ $$$$=\frac{\frac{\mathrm{2}\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}−\mathrm{2}}{\frac{\mathrm{4}}{\mathrm{2}−\sqrt{\mathrm{3}}}−\mathrm{1}}=\frac{\mathrm{2}\left(\sqrt{\mathrm{3}}−\mathrm{2}+\sqrt{\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}\right)}{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$${with}\:{R}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{\sqrt{\mathrm{3}}−\mathrm{2}+\sqrt{\mathrm{3}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}}{\mathrm{2}+\sqrt{\mathrm{3}}}\approx\mathrm{0}.\mathrm{168} \\ $$
Commented by Tawa11 last updated on 22/Jan/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
