Question Number 164820 by Avijit007 last updated on 22/Jan/22
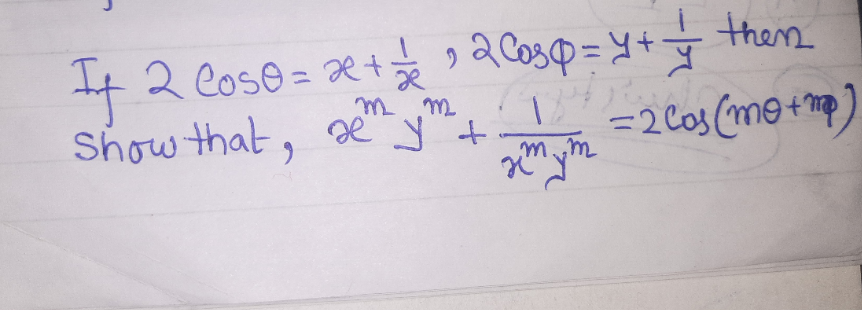
Answered by Ar Brandon last updated on 22/Jan/22
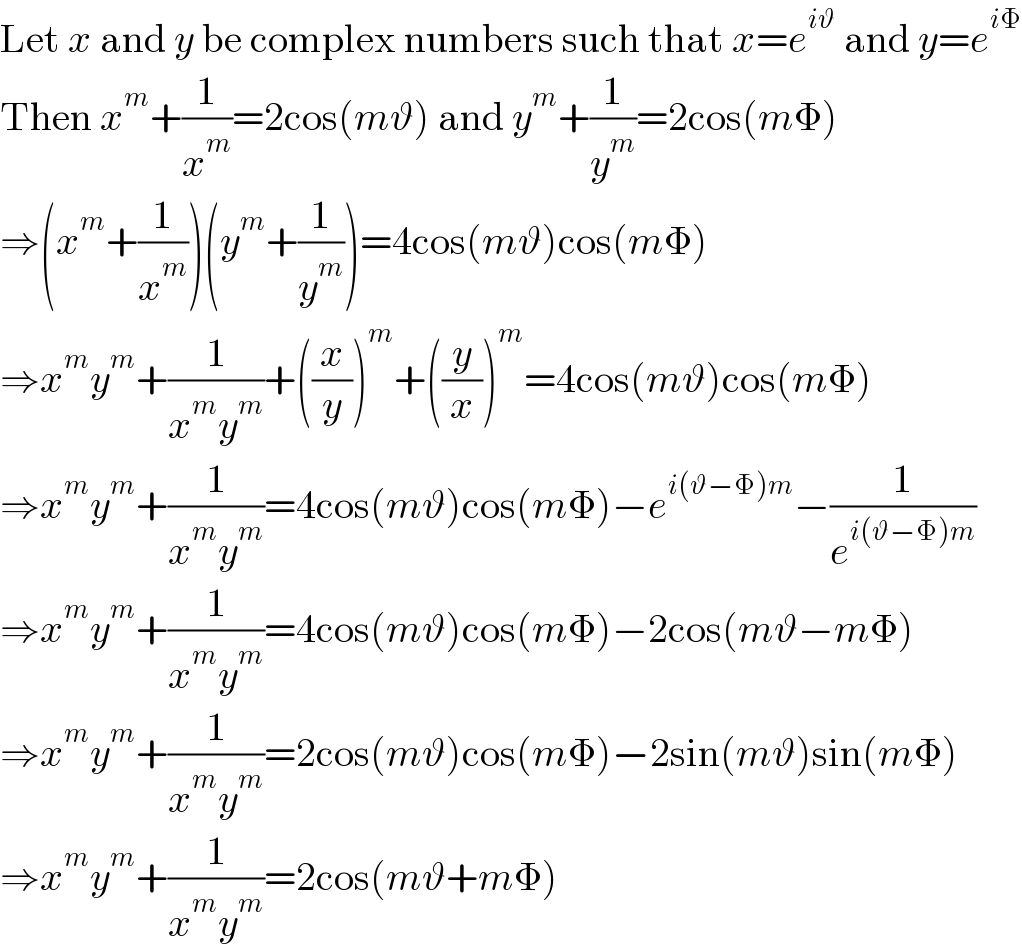
$$\mathrm{Let}\:{x}\:\mathrm{and}\:{y}\:\mathrm{be}\:\mathrm{complex}\:\mathrm{numbers}\:\mathrm{such}\:\mathrm{that}\:{x}={e}^{{i}\vartheta} \:\mathrm{and}\:{y}={e}^{{i}\Phi} \\ $$$$\mathrm{Then}\:{x}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} }=\mathrm{2cos}\left({m}\vartheta\right)\:\mathrm{and}\:{y}^{{m}} +\frac{\mathrm{1}}{{y}^{{m}} }=\mathrm{2cos}\left({m}\Phi\right) \\ $$$$\Rightarrow\left({x}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} }\right)\left({y}^{{m}} +\frac{\mathrm{1}}{{y}^{{m}} }\right)=\mathrm{4cos}\left({m}\vartheta\right)\mathrm{cos}\left({m}\Phi\right) \\ $$$$\Rightarrow{x}^{{m}} {y}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} {y}^{{m}} }+\left(\frac{{x}}{{y}}\right)^{{m}} +\left(\frac{{y}}{{x}}\right)^{{m}} =\mathrm{4cos}\left({m}\vartheta\right)\mathrm{cos}\left({m}\Phi\right) \\ $$$$\Rightarrow{x}^{{m}} {y}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} {y}^{{m}} }=\mathrm{4cos}\left({m}\vartheta\right)\mathrm{cos}\left({m}\Phi\right)−{e}^{{i}\left(\vartheta−\Phi\right){m}} −\frac{\mathrm{1}}{{e}^{{i}\left(\vartheta−\Phi\right){m}} } \\ $$$$\Rightarrow{x}^{{m}} {y}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} {y}^{{m}} }=\mathrm{4cos}\left({m}\vartheta\right)\mathrm{cos}\left({m}\Phi\right)−\mathrm{2cos}\left({m}\vartheta−{m}\Phi\right) \\ $$$$\Rightarrow{x}^{{m}} {y}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} {y}^{{m}} }=\mathrm{2cos}\left({m}\vartheta\right)\mathrm{cos}\left({m}\Phi\right)−\mathrm{2sin}\left({m}\vartheta\right)\mathrm{sin}\left({m}\Phi\right) \\ $$$$\Rightarrow{x}^{{m}} {y}^{{m}} +\frac{\mathrm{1}}{{x}^{{m}} {y}^{{m}} }=\mathrm{2cos}\left({m}\vartheta+{m}\Phi\right) \\ $$
