Menu Close

Question-16483

Tinku Tara 0 Comments
Pin




Question Number 16483 by RasheedSoomro last updated on 23/Jun/17
Commented by RasheedSoomro last updated on 23/Jun/17
Thanks sir for mentioning mistake. The figure has been changed.
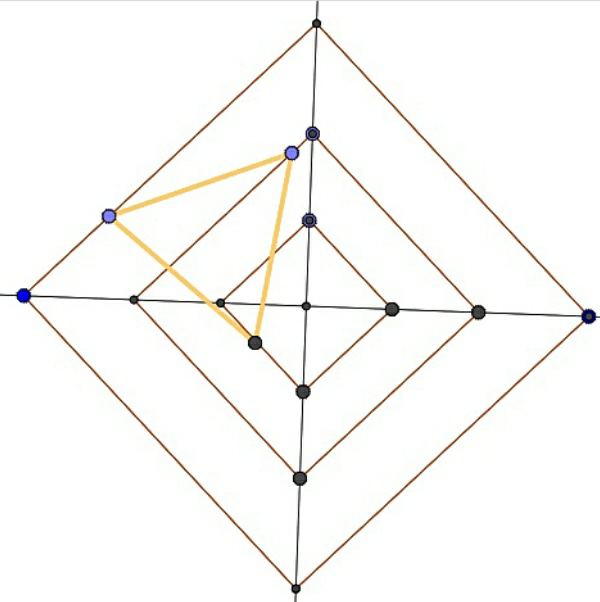
$$\mathrm{Thanks}\:\mathrm{sir}\:\mathrm{for}\:\mathrm{mentioning}\:\mathrm{mistake}. \\ $$$$\mathrm{The}\:\mathrm{figure}\:\mathrm{has}\:\mathrm{been}\:\mathrm{changed}. \\ $$
Commented by RasheedSoomro last updated on 23/Jun/17
There are three concentric squares. Construct by ruler & compass an equilateral triangle whose vertices are on different squares and which is (i)maximum (ii)minimum This question is posted to show only a variant of some past questions. If its answering is too laborious , pl don′t solve it.
$$\mathrm{There}\:\mathrm{are}\:\mathrm{three}\:\mathrm{concentric}\:\mathrm{squares}. \\ $$$$\mathrm{Construct}\:\mathrm{by}\:\mathrm{ruler}\:\&\:\mathrm{compass}\: \\ $$$$\mathrm{an}\:\mathrm{equilateral}\:\mathrm{triangle}\:\mathrm{whose}\:\mathrm{vertices}\:\mathrm{are}\:\mathrm{on} \\ $$$$\mathrm{different}\:\mathrm{squares}\:\mathrm{and}\:\mathrm{which}\:\mathrm{is}\:\left(\mathrm{i}\right)\mathrm{maximum} \\ $$$$\left(\mathrm{ii}\right)\mathrm{minimum} \\ $$$$\mathrm{This}\:\mathrm{question}\:\mathrm{is}\:\mathrm{posted}\:\mathrm{to}\:\mathrm{show}\:\mathrm{only}\:\mathrm{a}\:\mathrm{variant} \\ $$$$\:\mathrm{of}\:\mathrm{some}\:\mathrm{past}\:\mathrm{questions}.\:\mathrm{If}\:\mathrm{its}\:\mathrm{answering}\:\mathrm{is}\:\mathrm{too} \\ $$$$\mathrm{laborious}\:,\:\mathrm{pl}\:\mathrm{don}'\mathrm{t}\:\mathrm{solve}\:\mathrm{it}. \\ $$
Commented by mrW1 last updated on 23/Jun/17
the question is interesting. it′s similar to the question with 3 parallel lines, but these 3 lines have limited range, so the answer is a little bit more difficult, and there is not always a solution, I think.
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{interesting}.\:\mathrm{it}'\mathrm{s}\:\mathrm{similar} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{question}\:\mathrm{with}\:\mathrm{3}\:\mathrm{parallel}\:\mathrm{lines}, \\ $$$$\mathrm{but}\:\mathrm{these}\:\mathrm{3}\:\mathrm{lines}\:\mathrm{have}\:\mathrm{limited}\:\mathrm{range}, \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{a}\:\mathrm{little}\:\mathrm{bit}\:\mathrm{more}\:\mathrm{difficult}, \\ $$$$\mathrm{and}\:\mathrm{there}\:\mathrm{is}\:\mathrm{not}\:\mathrm{always}\:\mathrm{a}\:\mathrm{solution},\:\mathrm{I} \\ $$$$\mathrm{think}. \\ $$
Commented by RasheedSoomro last updated on 23/Jun/17
Actually the question is to determine three points on three squares which are pairwise equidistant from each other. By experimenting with geogebra I thought a possibility of existing such points. I think that the method suggested by you in some past questions will also be successful here. However to determine minimum/maximum size-triangle by ruler & compass is doubtful. ..... My first diagram was wrong and now I have repaced it. THANKS for taking interest Sir!
$$\mathrm{Actually}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{to}\:\mathrm{determine} \\ $$$$\mathrm{three}\:\mathrm{points}\:\mathrm{on}\:\mathrm{three}\:\mathrm{squares}\:\mathrm{which} \\ $$$$\mathrm{are}\:\mathrm{pairwise}\:\mathrm{equidistant}\:\mathrm{from}\:\mathrm{each}\:\mathrm{other}. \\ $$$$\mathrm{By}\:\mathrm{experimenting}\:\mathrm{with}\:\mathrm{geogebra}\:\mathrm{I}\:\mathrm{thought} \\ $$$$\mathrm{a}\:\mathrm{possibility}\:\mathrm{of}\:\mathrm{existing}\:\mathrm{such}\:\mathrm{points}. \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{that}\:\mathrm{the}\:\mathrm{method}\:\mathrm{suggested}\:\mathrm{by}\:\mathrm{you} \\ $$$$\mathrm{in}\:\mathrm{some}\:\mathrm{past}\:\mathrm{questions}\:\mathrm{will}\:\mathrm{also}\:\mathrm{be}\:\mathrm{successful} \\ $$$$\mathrm{here}. \\ $$$$\mathrm{However}\:\mathrm{to}\:\mathrm{determine}\:\mathrm{minimum}/\mathrm{maximum} \\ $$$$\mathrm{size}-\mathrm{triangle}\:\mathrm{by}\:\boldsymbol{\mathrm{ruler}}\:\&\:\boldsymbol{\mathrm{compass}}\:\mathrm{is}\:\mathrm{doubtful}. \\ $$$$….. \\ $$$$\mathrm{My}\:\mathrm{first}\:\mathrm{diagram}\:\mathrm{was}\:\mathrm{wrong}\:\mathrm{and}\:\mathrm{now}\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{repaced}\:\mathrm{it}. \\ $$$$\mathcal{THANKS}\:\:\:\mathrm{for}\:\mathrm{taking}\:\mathrm{interest}\:\:\mathcal{S}{ir}! \\ $$
Commented by mrW1 last updated on 23/Jun/17
Commented by RasheedSoomro last updated on 23/Jun/17
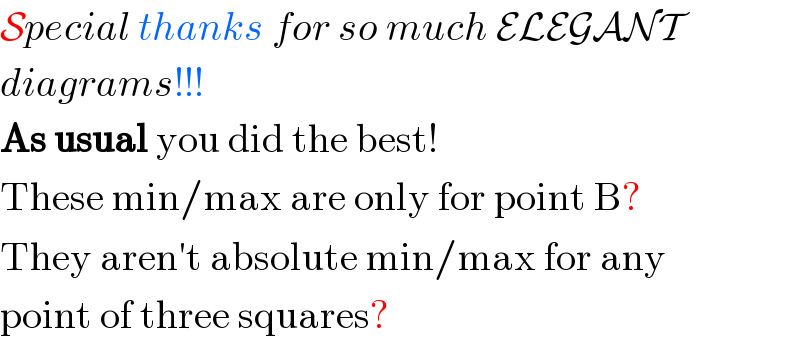
Special thanks for so much ELEGANT diagrams!!! As usual you did the best! These min/max are only for point B? They aren′t absolute min/max for any point of three squares?
$$\mathcal{S}{pecial}\:{thanks}\:{for}\:{so}\:{much}\:\mathcal{ELEGANT}\:\: \\ $$$${diagrams}!!! \\ $$$$\boldsymbol{\mathrm{As}}\:\boldsymbol{\mathrm{usual}}\:\mathrm{you}\:\mathrm{did}\:\mathrm{the}\:\mathrm{best}! \\ $$$$\mathrm{These}\:\mathrm{min}/\mathrm{max}\:\mathrm{are}\:\mathrm{only}\:\mathrm{for}\:\mathrm{point}\:\mathrm{B}? \\ $$$$\mathrm{They}\:\mathrm{aren}'\mathrm{t}\:\mathrm{absolute}\:\mathrm{min}/\mathrm{max}\:\mathrm{for}\:\mathrm{any} \\ $$$$\mathrm{point}\:\mathrm{of}\:\mathrm{three}\:\mathrm{squares}? \\ $$
Commented by mrW1 last updated on 23/Jun/17
Thanks for your compliment! To find the min. the point on the second square should be as close to the point on the first square (A) as possible. To find the max. the point on the second square should be as far from the point on the first square (B) as possible. So the min. and max. shown in the figure are the absolute min. and max. in this case. Certainly one can construct more identical such min. and identical such max. due to symmetry. But no smaller or bigger equilateral triangles can be constructed than the min. or max. shown.
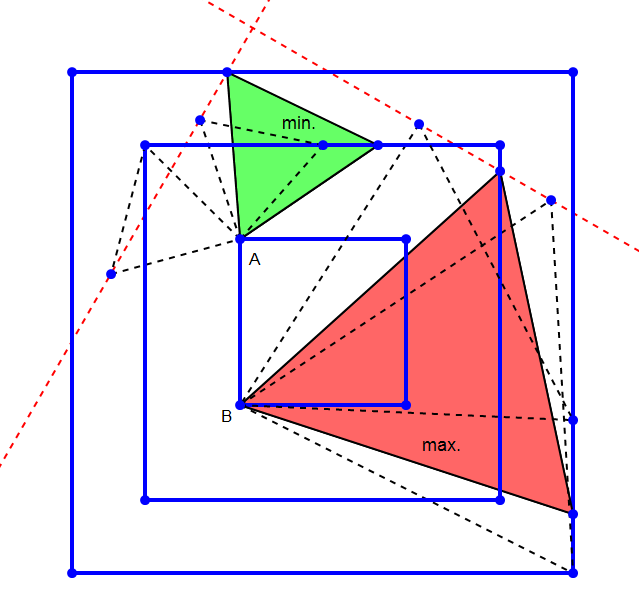
$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{compliment}! \\ $$$$\mathrm{To}\:\mathrm{find}\:\mathrm{the}\:\mathrm{min}.\:\mathrm{the}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{square}\:\mathrm{should}\:\mathrm{be}\:\mathrm{as}\:\mathrm{close}\:\mathrm{to}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{first}\:\mathrm{square}\:\left(\mathrm{A}\right)\:\mathrm{as}\:\mathrm{possible}. \\ $$$$\mathrm{To}\:\mathrm{find}\:\mathrm{the}\:\mathrm{max}.\:\mathrm{the}\:\mathrm{point}\:\mathrm{on}\:\mathrm{the}\:\mathrm{second} \\ $$$$\mathrm{square}\:\mathrm{should}\:\mathrm{be}\:\mathrm{as}\:\mathrm{far}\:\mathrm{from}\:\mathrm{the}\:\mathrm{point} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{first}\:\mathrm{square}\:\left(\mathrm{B}\right)\:\mathrm{as}\:\mathrm{possible}. \\ $$$$\mathrm{So}\:\mathrm{the}\:\mathrm{min}.\:\mathrm{and}\:\mathrm{max}.\:\mathrm{shown}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{figure}\:\mathrm{are}\:\mathrm{the}\:\mathrm{absolute}\:\mathrm{min}.\:\mathrm{and}\:\mathrm{max}. \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}.\:\mathrm{Certainly}\:\mathrm{one}\:\mathrm{can}\:\mathrm{construct} \\ $$$$\mathrm{more}\:\mathrm{identical}\:\mathrm{such}\:\mathrm{min}.\:\mathrm{and}\:\mathrm{identical} \\ $$$$\mathrm{such}\:\mathrm{max}.\:\mathrm{due}\:\mathrm{to}\:\mathrm{symmetry}.\:\mathrm{But}\:\mathrm{no} \\ $$$$\mathrm{smaller}\:\mathrm{or}\:\mathrm{bigger}\:\mathrm{equilateral}\:\mathrm{triangles} \\ $$$$\mathrm{can}\:\mathrm{be}\:\mathrm{constructed}\:\mathrm{than}\:\mathrm{the}\:\mathrm{min}.\:\mathrm{or} \\ $$$$\mathrm{max}.\:\mathrm{shown}. \\ $$
Commented by RasheedSoomro last updated on 23/Jun/17
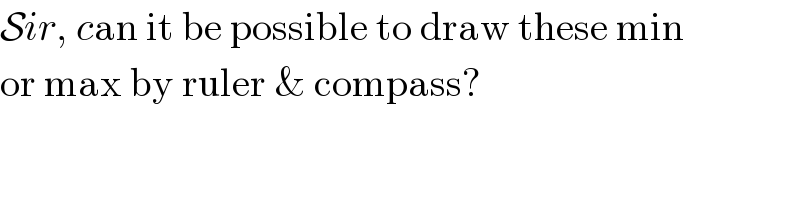
Sir, can it be possible to draw these min or max by ruler & compass?
$$\mathcal{S}{ir},\:{c}\mathrm{an}\:\mathrm{it}\:\mathrm{be}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{draw}\:\mathrm{these}\:\mathrm{min} \\ $$$$\mathrm{or}\:\mathrm{max}\:\mathrm{by}\:\mathrm{ruler}\:\&\:\mathrm{compass}? \\ $$
Commented by mrW1 last updated on 23/Jun/17
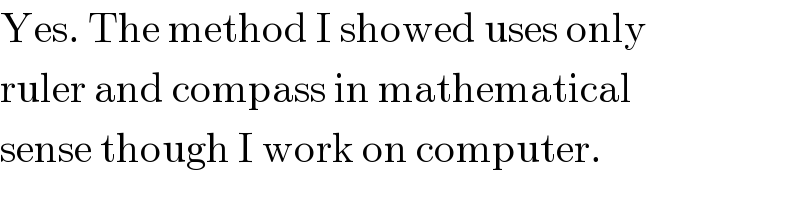
Yes. The method I showed uses only ruler and compass in mathematical sense though I work on computer.
$$\mathrm{Yes}.\:\mathrm{The}\:\mathrm{method}\:\mathrm{I}\:\mathrm{showed}\:\mathrm{uses}\:\mathrm{only} \\ $$$$\mathrm{ruler}\:\mathrm{and}\:\mathrm{compass}\:\mathrm{in}\:\mathrm{mathematical} \\ $$$$\mathrm{sense}\:\mathrm{though}\:\mathrm{I}\:\mathrm{work}\:\mathrm{on}\:\mathrm{computer}. \\ $$
Commented by mrW1 last updated on 23/Jun/17
Commented by mrW1 last updated on 24/Jun/17
We start at point B. On the side of third square opposite to B we select two arbitrary points P_1 and P_2 and construct equilateral triangles ΔBP_1 Q_1 and ΔBP_2 Q_2 . Connecting Q_1 and Q_2 we get a line which intersects with the side of second square opposite to B at point C. Using C as center and CB as radius we draw a circle which intersects the side of third square at point D. ΔBCD is then the requested equilateral triangle. All these operations use only ruler and compass.
$$\mathrm{We}\:\mathrm{start}\:\mathrm{at}\:\mathrm{point}\:\mathrm{B}. \\ $$$$\mathrm{On}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{third}\:\mathrm{square}\:\mathrm{opposite}\:\mathrm{to}\: \\ $$$$\mathrm{B}\:\mathrm{we}\:\mathrm{select}\:\mathrm{two}\:\mathrm{arbitrary}\:\mathrm{points}\:\mathrm{P}_{\mathrm{1}} \:\mathrm{and}\: \\ $$$$\mathrm{P}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{construct}\:\mathrm{equilateral}\:\mathrm{triangles} \\ $$$$\Delta\mathrm{BP}_{\mathrm{1}} \mathrm{Q}_{\mathrm{1}} \:\mathrm{and}\:\Delta\mathrm{BP}_{\mathrm{2}} \mathrm{Q}_{\mathrm{2}} .\:\mathrm{Connecting} \\ $$$$\mathrm{Q}_{\mathrm{1}} \:\mathrm{and}\:\mathrm{Q}_{\mathrm{2}} \:\mathrm{we}\:\mathrm{get}\:\mathrm{a}\:\mathrm{line}\:\mathrm{which}\:\mathrm{intersects} \\ $$$$\mathrm{with}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{second}\:\mathrm{square}\:\mathrm{opposite} \\ $$$$\mathrm{to}\:\mathrm{B}\:\mathrm{at}\:\mathrm{point}\:\mathrm{C}.\:\mathrm{Using}\:\mathrm{C}\:\mathrm{as}\:\mathrm{center}\:\mathrm{and} \\ $$$$\mathrm{CB}\:\mathrm{as}\:\mathrm{radius}\:\mathrm{we}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{circle}\:\mathrm{which} \\ $$$$\mathrm{intersects}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{third}\:\mathrm{square}\:\mathrm{at} \\ $$$$\mathrm{point}\:\mathrm{D}.\:\Delta\mathrm{BCD}\:\mathrm{is}\:\mathrm{then}\:\mathrm{the}\:\mathrm{requested}\: \\ $$$$\mathrm{equilateral}\:\mathrm{triangle}. \\ $$$$\mathrm{All}\:\mathrm{these}\:\mathrm{operations}\:\mathrm{use}\:\mathrm{only}\:\mathrm{ruler}\:\mathrm{and} \\ $$$$\mathrm{compass}. \\ $$
Commented by RasheedSoomro last updated on 24/Jun/17
[(T,H,A,N,K,S),(H,⌈,�,�,⌉,K),(A,∣,⌈,⌉,∣,N),(N,∣,⌊,⌋,∣,A),(K,⌊,_,_,⌋,H),(S,K,N,A,H,T) ]! Appriciate your knowledge of geometry! Appriciate your knowledge-sharing skill! Appriciate your sharing-sprit!
$$\begin{bmatrix}{\mathcal{T}}&{\mathcal{H}}&{\mathcal{A}}&{\mathcal{N}}&{\mathcal{K}}&{\mathcal{S}}\\{\mathcal{H}}&{\lceil}&{}&{}&{\rceil}&{\mathcal{K}}\\{\mathcal{A}}&{\mid}&{\lceil}&{\rceil}&{\mid}&{\mathcal{N}}\\{\mathcal{N}}&{\mid}&{\lfloor}&{\rfloor}&{\mid}&{\mathcal{A}}\\{\mathcal{K}}&{\lfloor}&{\_}&{\_}&{\rfloor}&{\mathcal{H}}\\{\mathcal{S}}&{\mathcal{K}}&{\mathcal{N}}&{\mathcal{A}}&{\mathcal{H}}&{\mathcal{T}}\end{bmatrix}! \\ $$$$\mathrm{Appriciate}\:\mathrm{your}\:\mathrm{knowledge}\:\mathrm{of}\:\mathrm{geometry}! \\ $$$$\mathrm{Appriciate}\:\mathrm{your}\:\mathrm{knowledge}-\mathrm{sharing}\:\mathrm{skill}! \\ $$$$\mathrm{Appriciate}\:\mathrm{your}\:\mathrm{sharing}-\mathrm{sprit}! \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *